江苏省2022年高考数学模拟题分类汇编-函数的奇偶性3

这是一份江苏省2022年高考数学模拟题分类汇编-函数的奇偶性3，共26页。试卷主要包含了单选题，多选题，填空题等内容，欢迎下载使用。
江苏省2022年高考数学模拟题分类汇编-函数的奇偶性

一、单选题
1．（2022·江苏省木渎高级中学模拟预测）下列函数既是奇函数，又是增函数的是（       ）
A． B． C． D．
2．（2022·江苏淮安·模拟预测）已知偶函数的定义域为R，导函数为，若对任意，都有恒成立，则下列结论正确的是（       ）
A． B． C． D．
3．（2022·江苏淮安·模拟预测）已知函数，则的图象大致是（       ）
A． B．
C． D．
4．（2022·江苏苏州·模拟预测）已知奇函数在点处的切线方程为，则（       ）
A．或1 B．或 C．或2 D．或
5．（2022·江苏连云港·模拟预测）已知函数的图象大致为（       ）
A． B．
C． D．
6．（2022·江苏·二模）已知函数为偶函数，则不等式的解集为（       ）
A． B．
C． D．
7．（2022·江苏南通·模拟预测）若函数为奇函数，则实数的值为（       ）
A．1 B．2 C． D．
8．（2022·江苏连云港·二模）已知函数是偶函数，则的值是（       ）
A． B． C．1 D．2
9．（2022·江苏江苏·二模）已知是定义域为R的偶函数，f(5.5)＝2，g(x)＝(x－1).若g(x＋1)是偶函数，则＝(       )
A．－3 B．－2 C．2 D．3
10．（2022·江苏·南京市宁海中学二模）函数在其定义域上的图象大致是（       ）
A． B． C． D．
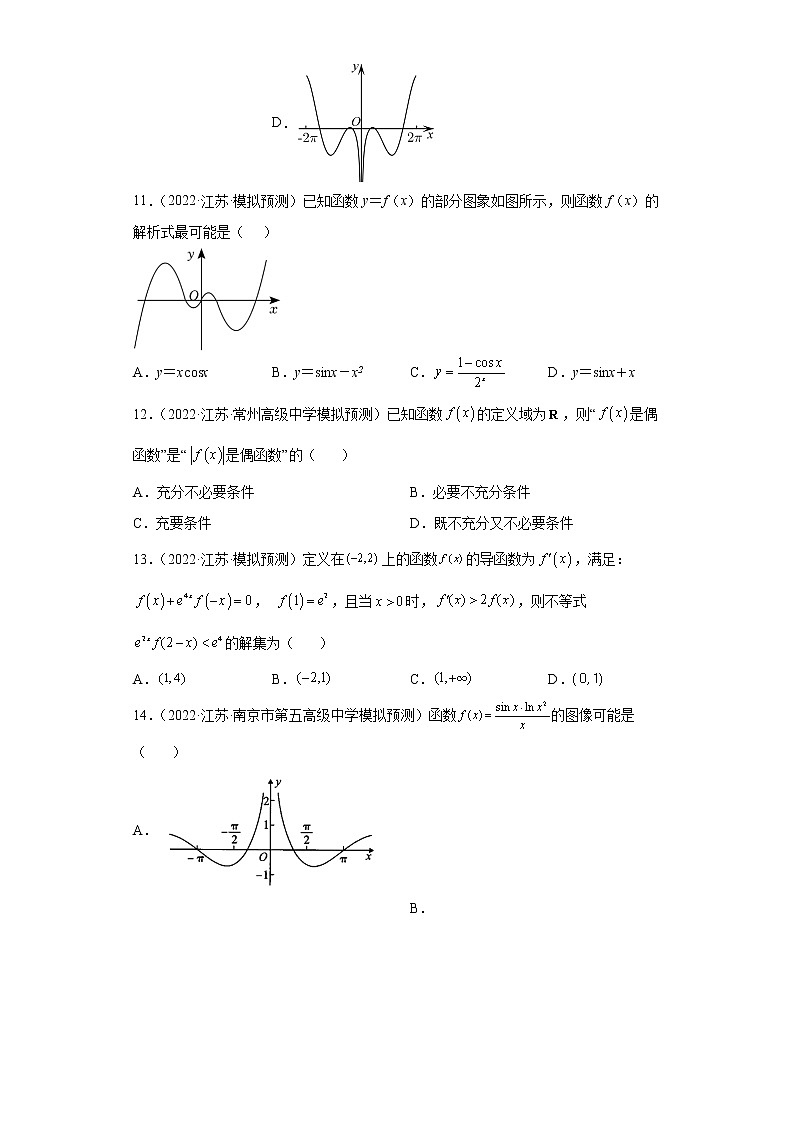
11．（2022·江苏·模拟预测）已知函数y＝f（x）的部分图象如图所示，则函数f（x）的解析式最可能是（     ）

A．y＝xcosx B．y＝sinx－x2 C． D．y＝sinx＋x
12．（2022·江苏·常州高级中学模拟预测）已知函数的定义域为，则“是偶函数”是“是偶函数”的（       ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分又不必要条件
13．（2022·江苏·模拟预测）定义在上的函数的导函数为，满足：， ，且当时，，则不等式的解集为（       ）
A． B． C． D．
14．（2022·江苏·南京市第五高级中学模拟预测）函数的图像可能是（       ）
A． B．
C． D．
15．（2022·江苏扬州·模拟预测）已知函数，若，则（       ）
A． B． C． D．
16．（2022·江苏·常州高级中学模拟预测）已知定义在上的函数是奇函数，当时，，则不等式的解集为（       ）
A． B． C． D．
17．（2022·江苏·苏州市第六中学校三模）函数在的图像大致为
A． B． C． D．

二、多选题
18．（2022·江苏盐城·三模）已知函数为上的奇函数，为偶函数，下列说法正确的有（       ）
A．图象关于直线对称 B．
C．的最小正周期为4 D．对任意都有
19．（2022·江苏·华罗庚中学三模）是定义在上的函数，若是奇函数，是偶函数，函数，则（       ）
A．当时， B．当时，
C． D．
20．（2022·江苏南京·模拟预测）（多选题）声音是由物体振动产生的声波，其中包含着正弦函数．纯音的数学模型是函数，我们听到的声音是由纯音合成的，称之为复合音．若一个复合音的数学模型是函数，则下列结论正确的是（       ）
A．的图象关于直线对称 B．在上是增函数
C．的最大值为 D．若，则
21．（2022·江苏南通·模拟预测）若函数同时具有性质：①对于任意的，，②为偶函数，则函数可能为（       ）
A． B． C． D．
22．（2022·江苏扬州·模拟预测）已知函数是定义在R上的奇函数，是偶函数，当，则下列说法中正确的有（       ）
A．函数关于直线对称
B．4是函数的周期
C．
D．方程恰有4不同的根
23．（2022·江苏·南京市宁海中学模拟预测）已知是定义在R上的偶函数，且对任意，有，当时，，则（       ）
A．是以2为周期的周期函数
B．点是函数的一个对称中心
C．
D．函数有3个零点
24．（2022·江苏泰州·模拟预测）已知定义在上的单调递增的函数满足：任意，有，，则（       ）
A．当时，
B．任意，
C．存在非零实数，使得任意，
D．存在非零实数，使得任意，
25．（2022·江苏江苏·一模）若函数，则关于的性质说法正确的有（       ）
A．偶函数 B．最小正周期为
C．既有最大值也有最小值 D．有无数个零点
26．（2022·江苏·南京市第五高级中学模拟预测）已知函数，，则（       ）
A．函数为偶函数
B．函数为奇函数
C．函数在区间上的最大值与最小值之和为0
D．设，则的解集为

三、填空题
27．（2022·江苏·南京市天印高级中学模拟预测）已知是定义在上的函数，若对任意，都有，且函数的图像关于直线对称，，则_______.
28．（2022·江苏江苏·三模）写出一个同时具有下列性质①②③的函数___________.①是定义域为的奇函数；②；③.
29．（2022·江苏·扬州中学模拟预测）已知是定义在R上的偶函数，当时，.若的图象与x轴恰有三个交点，则实数a的值为___________.
30．（2022·江苏江苏·二模）已知定义在上的奇函数满足，当时，，若对一切恒成立，则实数的最大值为___________.
31．（2022·江苏南通·模拟预测）已知是奇函数，且当时，，则___________．
32．（2022·江苏泰州·一模）写出一个同时具有下列性质①②③的三次函数_________.
①为奇函数；②存在3个不同的零点；③在上是增函数.
33．（2022·江苏江苏·一模）若是奇函数，则___________.
34．（2022·江苏·南京市宁海中学二模）已知奇函数满足条件，且当 时，，则 ______ ．

参考答案：
1．B
【分析】根据函数的单调性和奇偶性性质逐项分析，即可选出答案.
【详解】解：由题意得：
对于选项A：函数是偶函数，故不符合题意；
对于选项B：函数是奇函数，且是单调递增函数，故符合题意；
对于选项C：函数是非奇非偶函数，故不符合题意；
对于选项D：根据幂函数的性质可知函数是奇函数，但不是单调递增函数，故不符合题意；
故选：B
2．C
【分析】令，结合条件可判断出在上单调递增，且函数为偶函数，进而可得.
【详解】令，则，则A错误；
令，则，
当时，由，
，则在上单调递增，
又因为偶函数的定义域为R，
∴为偶函数，在上单调递增，
，，故B错误；
，，故C正确；
由题意，不妨假设(c为常数)符合题意，此时，故D错误.
故选：C.
3．D
【分析】确定函数的奇偶性，再利用函数值的正负逐一排除即可.
【详解】∵，
∴，定义域关于原点对称，
故是偶函数，排除A，
当时，，即，
当时，又有，因此，排除B，C.
故选：D．
4．D
【分析】由函数为奇函数可得，根据切线的斜率为0建立方程求出即可得解.
【详解】由可得，
因为，所以，解得.
所以，故切线斜率，
又，所以，解得或，
所以或.
故选：D
5．D
【分析】利用函数的奇偶性排除部分选项，再判断在上值的符号作答.
【详解】函数的定义域为R，，即函数是R上的奇函数，B不满足；
而当时，，，选项A，C不满足，选项D符合题意.
故选：D
6．B
【分析】先求得参数a的值，再去求不等式的解集
【详解】因为为偶函数，所以，即
解之得，经检验符合题意.则
由，可得
故的解集为，
故选：B.
7．D
【分析】根据题意可得，计算可得，经检验均符合题意，即可得解.
【详解】由为奇函数，
所以，
所以，可得，
解得，
当时，的定义域为，符合题意，
当时，的定义域为符合题意，
故选：D
8．A
【分析】先求出函数的定义域，然后根据偶函数的定义取特殊值求解
【详解】函数的定义域为，
因为函数是偶函数，
所以，
所以，
，所以，
得，
故选：A
9．D
【分析】根据g(x＋1)得到g(x)关于x＝1对称，得到，结合g(x)＝(x－1)和f(x)为偶函数即可得f(x)周期为4，故可求出f(2.5)＝2，则即可求值﹒
【详解】为偶函数，则关于对称，即，
即，即，
关于对称，又f(x)是定义域为R的偶函数，
∴，
∴f(x－4)＝f[(x－2)－2]＝－f(x－2)＝－[－f(x)]＝f(x)，即f(x－4)＝f(x)，
周期为，
∴，
.
故选：D.
10．C
【分析】利用函数的奇偶性，以及特殊点的函数值符号即可由排除法选出正确图象.
【详解】，
所以函数是奇函数，图象关于原点对称，故排除选项，
因为当时，，，
又因为时，，所以，
，，所以，故在区间与轴有三个交点，故排除.
故选：C.
11．A
【分析】由图象判断函数的奇偶性，以及函数值的符号，运用排除法可得结论.
【详解】由f（x）的图象关于原点对称，可得f（x）为奇函数，
对于选项B，f（x）＝sinx－x2，f（－x）＝－sinx－x2≠－f（x），f（x）不为奇函数，故排除B；
对于选项C，f（x）＝，f（－x）＝＝2x（1－cosx）≠－f（x），f（x）不为奇函数，故排除C；
对于选项D，f（x）＝x＋sinx，f（－x）＝－sinx－x＝－f（x），可得f（x）为奇函数，
由f（x）＝0，可得sinx＝－x，f（0）＝0，由y＝sinx和y＝－x的图象可知它们只有一个交点，故排除D；
对于选项A，f（x）＝xcosx，f（－x）＝－xcos（－x）＝－xcosx＝－f（x），可得f（x）为奇函数，
且f（x）＝0时，x＝0或x＝kπ＋（k∈Z），f（）＜0，f（π）＜0，
故选项A最可能正确.
故选：A.
12．A
【分析】根据偶函数的图像性质，结合充分，必要条件的定义进行判断
【详解】偶函数的图像关于轴对称，奇函数图像关于原点对称，根据这一特征，若是偶函数，则是偶函数，若是奇函数，也是偶函数，所以“是偶函数”是“是偶函数”的充分不必要条件
故选：A
13．A
【分析】由给定的不等式构造函数对求导，根据已知条件可判断非得单调性，将所求解不等式转化为有关的不等式，利用单调性脱去即可求解.
【详解】令，则可得
所以是上的奇函数，
，
当时，，所以，
是上单调递增，
所以是上单调递增，
因为，
由可得即，
由是上单调递增，可得 解得：，
所以不等式的解集为，
故选：A.
【点睛】关键点点睛：本题解题的关键点是：构造函数，根据已知条件判断的奇偶性和单调性，利用单调性解不等式 .
14．B
【分析】根据函数的奇偶性排除C、D，再结合排除A，即可求解.
【详解】由题意得函数的定义域是关于原点对称
又由，所以是偶函数，
所以函数的图像关于y轴对称，故排除C、D；
当时，，故排除A.
故选：B.
15．A
【解析】先判断函数的奇偶性和单调性，再分析得解.
【详解】由题得函数的定义域为R.
,
所以函数是偶函数.
当时，，
因为，所以，所以函数在上单调递增，
因为函数是偶函数，所以函数在上单调递减，在上单调递增.
如果，则，
因为，所以，与已知相符；
如果，则，所以,与已知相符；
如果，因为，所以，
所以，与已知矛盾；
如果，因为，所以，
所以，与已知矛盾；
当之中有一个为零时，不妨设， ，
，显然不成立.
故选：A
【点睛】方法点睛：对于函数的问题，要灵活利用函数的奇偶性和单调性分析函数的问题，利用函数的图象和性质分析函数的问题.
16．D
【解析】本题首先可根据题意得出函数的图像关于点中心对称且，然后根据基本不等式得出，则函数在上单调递增，最后将不等式转化为或，通过计算即可得出结果.
【详解】因为函数是定义在上的奇函数，
所以函数的图像关于点中心对称，且，
当时，，
则，当且仅当时取等号，
故，函数在上单调递增，
因为函数的图像关于点中心对称，
所以函数在上单调递增，
不等式可化为或，
，即，解得，
，即，解得，
故不等式的解集为，
故选：D.
【点睛】关键点点睛：若函数是偶函数，则函数的图像关于直线对称；若函数是奇函数，则函数的图像关于点中心对称，考查通过基本不等式求最值，考查根据导函数判断函数单调性，是难题.
17．B
【分析】由分子、分母的奇偶性，易于确定函数为奇函数，由的近似值即可得出结果．
【详解】设，则，所以是奇函数，图象关于原点成中心对称，排除选项C．又排除选项D；，排除选项A，故选B．
【点睛】本题通过判断函数的奇偶性，缩小考察范围，通过计算特殊函数值，最后做出选择．本题较易，注重了基础知识、基本计算能力的考查．
18．ABD
【分析】由奇偶性知的对称中心为、对称轴为，进而推得，即可判断各选项的正误.
【详解】由的对称中心为，对称轴为，
则也关于直线对称且，A、D正确，
由A分析知：，故，
所以，
所以的周期为4，则，B正确；
但不能说明最小正周期为4，C错误；
故选：ABD
19．AD
【分析】先求出，对四个选项一一一验证：
对于A、B：利用代入法求解析式,即可判断；对于C:分别求出和，求出.即可判断;对于D：由，利用等比数列的求和公式即可求得.
【详解】因为是奇函数,是偶函数,则有，解得.
对于A：任取，则，所以.故A正确；
对于B：任取，则，所以.故B错误；
对于C:当x∈(2,3)时,有x-1∈(1,2),x-2∈(0,1).所以，则有，，故.故C错误;
对于D：由C的结论, ，则.故D正确.
故选：AD
20．BCD
【分析】利用对称性定义推理判断A；由与在上单调性判断B；借助导数求出在周期长的区间上的最大值判断C；由在周期长的区间上的最大最小值判断D作答.
【详解】对于A，因，则的图象关于对称，不关于对称，A错误；
对于B，因与在上都是增函数，则在上是增函数，B正确；
对于C，因，即是奇函数，
又与的最小正周期分别为与，则的正周期为，
当时，，令，得，即，
当时，，当时，，则在上递增，在上递减，
因此，在上的最大值为，由是奇函数得在上的最大值为，
由的正周期为，则在R上的最大值为，C正确；
对于D，由选项C得，，，，
又，则，
所以当时，，D正确．
故选：BCD
21．AC
【分析】首先判断B为奇函数，再利用基本不等式判断A、C，利用特殊值判断D；
【详解】解：对于B：，
故为奇函数，故B错误，A，C，D为偶函数；
对于A，，故A对
对于C，
，故C对
对于D，，时，，故D错，
故选：AC．
22．ABD
【分析】根据奇偶性的定义，结合函数的对称性，即可判断A的正误；根据题意，结合函数的周期性，可判断B的正误；根据函数的周期性，结合解析式，即可判断C的正误；分别作出和的图象，即可判断D的正误，即可得答案.
【详解】对于A：因为是偶函数，
所以，即
所以关于对称，故A正确.
对于B：因为，
所以，
所以，即周期，故B正确
对于C：
所以，故C错误；
对于D：因为，且关于直线对称，
根据对称性可以作出上的图象，
又，根据对称性，可作出上的图象，
又的周期，
作出图象与图象，如下图所示：

所以与有4个交点，故D正确.
故选： ABD
23．BD
【分析】首先根据函数的对称性求出的周期和对称中心，然后求得.利用图象法即可判断D.
【详解】依题意，为偶函数，
且，有，即关于对称，
则
，
所以是周期为4的周期函数，故A错误；
因为的周期为4，关于对称，
所以是函数的一个对称中心，故B正确；
因为的周期为4，则，，
所以，故C错误；
作函数和的图象如下图所示，

由图可知，两个函数图象有3个交点，
所以函数有3个零点，故D正确.
故选：BD.
24．ABD
【分析】令可推导得，结合的值可知A正确；令可推导得，结合可推导知B正确；根据单调性可知C错误；当时，根据的对称中心及其在时的值域可确定时满足，知D正确.
【详解】对于A，令，则，即，
又，；
令得：，，，，
则由可知：当时，，A正确；
对于B，令，则，即，
，
由A的推导过程知：，，B正确；
对于C，为上的增函数，
当时，，则；当时，，则，
不存在非零实数，使得任意，，C错误；
对于D，当时，；
由，知：关于，成中心对称，则当时，为的对称中心；
当时，为上的增函数，，，，
；
由图象对称性可知：此时对任意，，D正确.
故选：ABD.
【点睛】关键点点睛：本题考查函数对称性的应用，解题关键是能够根据已知关系式确定的对称中心，同时采用赋值的方式确定所满足的其他关系式，从而结合对称性和其他函数关系式来确定所具有的其他性质.
25．CD
【分析】根据二倍角的余弦公式，结合正弦函数的单调性、周期的定义、偶函数的定义、零点的定义逐一判断即可.
【详解】A：因为，所以该函数不是偶函数，因此本选项说法不正确；
B：因为，所以该函数最小正周期不是，因此本选项说法不正确；
C：因为，当时，该函数有最大值，当时，该函数有最小值，因此本选项说法正确；
D：，则有，解得，或，
即，或，或，因此本选项说法正确，
故选：CD
26．BCD
【分析】根据题意，利用奇偶性，单调性，依次分析选项是否正确，即可得到答案
【详解】对于A：，定义域为，，
则为奇函数，故A错误；
对于B：，定义域为，
，
则为奇函数，故B正确；
对于C：，，都为奇函数，
则为奇函数，
在区间上的最大值与最小值互为相反数，
必有在区间上的最大值与最小值之和为0，故C正确；
对于D：，则在上为减函数，
，则在上为减函数，
则在上为减函数，
若即，
则必有，解得，
即的解集为，故D正确；
故选：BCD
27．3
【分析】先由函数的图像关于直线对称，得到函数是偶函数，则有；
又令代入，求得函数的周期为，利用函数周期化简即可求值.
【详解】因为函数的图像关于直线对称，所以函数的图像关于直线对称，即函数是偶函数，则有；
因为对任意，都有，
令，得，
所以对任意，都有，即函数的周期为，
则，
故答案为：.
28．（答案不唯一）
【分析】根据满足的条件写出一个函数即可.
【详解】由条件①②③可知函数对称轴为，定义域为R的奇函数，可写出满足条件的函数.
故答案为：（答案不唯一）
29．2
【分析】根据偶函数的对称性知在、上各有一个零点且，讨论a值结合导数研究的零点情况，即可得结果.
【详解】由偶函数的对称性知：在、上各有一个零点且，
所以，则或，
当时，在上，则，
所以在上递增，，故无零点，不合要求；
当时，在上，则，
所以在上递减，在上递增，
则且，，故上有一个零点，符合要求；
综上，.
故答案为：2
30．##0.25
【分析】根据题设条件画出函数的图象，结合图象可求实数的最大值.
【详解】因为，故的图象关于中心对称
当时，，
故的图象如图所示：

结合图象可得：只需当时，即可，
即，故，
故答案为：.
31．##
【分析】利用奇函数的性质代入求值即可.
【详解】．
故答案为：.
32．
【分析】根据已知写出符合三个条件的函数，验证即可.
【详解】，为奇函数，有三个零点0，，
，时，，即在为增函数，
①②③都满足，∴.
故答案为：
33．
【分析】根据奇函数的性质，结合奇函数的定义进行求解即可.
【详解】因为是奇函数，
所以有，即，即，
因为，
所以函数是奇函数，
故答案为：
34．
【分析】首先得到函数的周期，再利用函数的周期和奇偶性，化简求值.
【详解】，，且函数是奇函数，所以化简
，
，，
.
故答案为：-2
【点睛】关键点点睛：本题的关键是利用函数的周期性和奇函数的性质化简.