江苏省2022年高考数学模拟题分类汇编-余弦函数的单调性、定义域、奇偶性、周期性、对称性

这是一份江苏省2022年高考数学模拟题分类汇编-余弦函数的单调性、定义域、奇偶性、周期性、对称性，共15页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
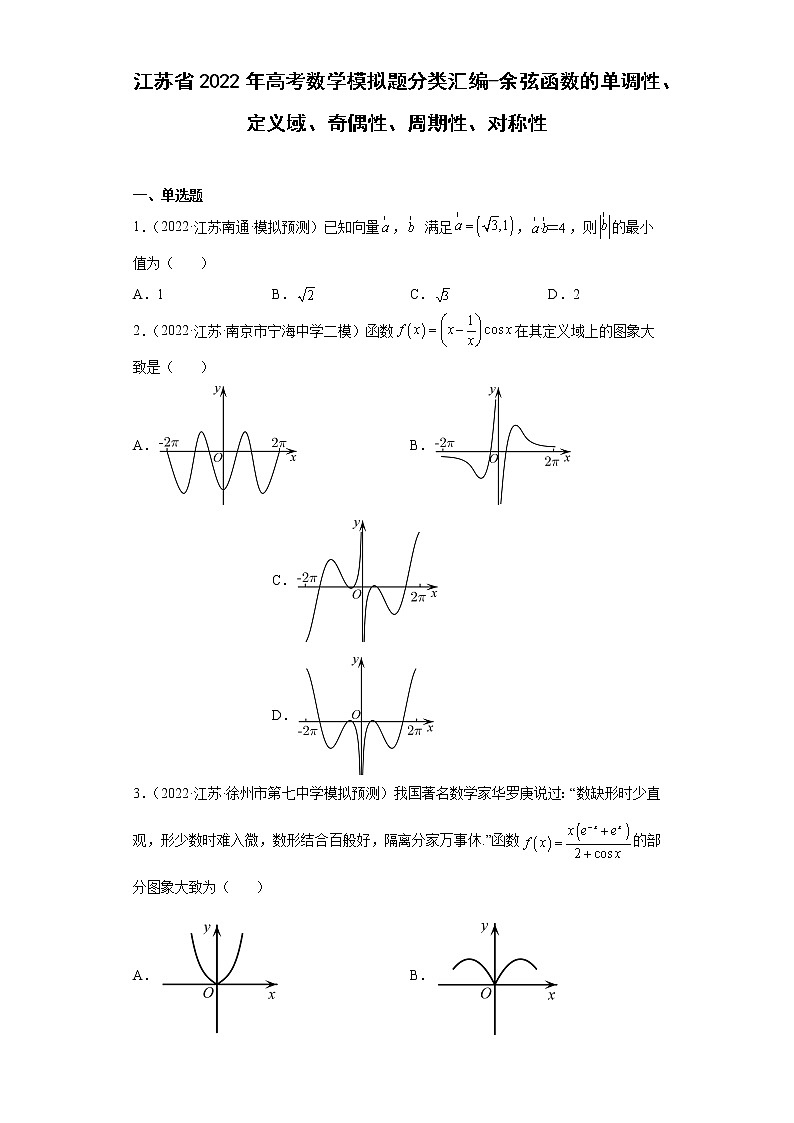
江苏省2022年高考数学模拟题分类汇编-余弦函数的单调性、定义域、奇偶性、周期性、对称性 一、单选题1．（2022·江苏南通·模拟预测）已知向量， 满足，，则的最小值为（       ）A．1 B． C． D．22．（2022·江苏·南京市宁海中学二模）函数在其定义域上的图象大致是（       ）A． B． C． D．3．（2022·江苏·徐州市第七中学模拟预测）我国著名数学家华罗庚说过：“数缺形时少直观，形少数时难入微，数形结合百般好，隔离分家万事休.”函数的部分图象大致为（       ）A． B．C． D．4．（2022·江苏连云港·模拟预测）如果函数满足，则的最小值是（       ）A． B． C． D．5．（2022·江苏·新沂市第一中学模拟预测）函数的一个对称中心是（       ）A． B． C． D．6．（2022·江苏常州·模拟预测）在中，满足，则下列说法正确的是（       ）A． B．C． D．7．（2022·江苏泰州·一模）已知，均为锐角，且，则（       ）A． B． C． D． 二、多选题8．（2022·江苏江苏·一模）下列函数中，最大值是1的函数有（       ）A． B．C． D．9．（2022·江苏无锡·模拟预测）关于函数的下列结论正确的是（       ）A．函数是偶函数 B．函数的周期是C．函数的最大值为 D．函数在上有无数个零点10．（2022·江苏苏州·模拟预测）已知函数，则（       ）A．是周期函数 B．是偶函数C．是上的增函数 D．的最小值为11．（2022·江苏·南京外国语学校模拟预测）已知函数=sin[cosx]+cos[sinx]，其中[x]表示不超过实数x的最大整数，下列结论中不正确的是（       ）A．的一个周期是2π B．是偶函数C．在单调递减 D．的最大值不大于12．（2022·江苏·南京市宁海中学二模）已知函数，则（       ）A．对任意正奇数n，f(x)为奇函数B．当n=3时，f(x)在[0，]上的最小值为C．当n=4时，f(x)的单调递增区间是D．对任意正整数n，f(x)的图象都关于直线对称13．（2022·江苏·模拟预测）设函数（，是常数，，），若在区间上具有单调性，且，则下列说法正确的是（       ）A．的最小正周期为πB．的单调递减区间为，C．图像的对称轴为直线，D．的图像可由的图像向左平移个单位长度得到14．（2022·江苏连云港·二模）已知函数，则（       ）A．函数的最小正周期为B．点是函数图象的一个对称中心C．将函数图象向左平移个单位长度，所得到的函数图象关于轴对称D．函数在区间上单调递减15．（2022·江苏·海安高级中学二模）已知，则（       ）A．    B．    C．    D．   16．（2022·江苏南通·模拟预测）已知定义在R上的函数的图象连续不间断，当时，，且当时，，则下列说法正确的是（       ）A．B．在上单调递减C．若，则D．若是的两个零点，且，则 三、填空题17．（2022·江苏无锡·模拟预测）写出一个最小正周期为1的偶函数______． 四、解答题18．（2022·江苏苏州·模拟预测）已知，函数．(1)讨论的导函数零点的个数；(2)若，求的取值范围．
参考答案：1．D【分析】利用向量的数量积公式和余弦函数的有界性即可求解.【详解】∵，∴，其中为向量，的夹角，即，当时，有最小值，故选:．2．C【分析】利用函数的奇偶性，以及特殊点的函数值符号即可由排除法选出正确图象.【详解】，所以函数是奇函数，图象关于原点对称，故排除选项，因为当时，，，又因为时，，所以，，，所以，故在区间与轴有三个交点，故排除.故选：C.3．C【解析】首先排除函数的奇偶性，再判断时的函数值的正负.【详解】，函数是奇函数，故排除AB，当时，，，所以，故排除D.故选：C4．B【分析】根据余弦函数的对称轴可得结果.【详解】因为函数满足，所以的图象关于对称，所以，，所以，，所以的最小值为.故选：B5．C【分析】根据两角和正弦余弦公式及二倍角的余弦公式，再结合余弦函数的性质即可求解.【详解】.由，得，此时.所以的对称中心为.当时，的一个对称中心为.故选：C.6．A【分析】推导出，利用余弦函数的单调性可判断A选项；利用特殊值法可判断BCD选项.【详解】对于A选项，因为，所以，，则，因为，所以，，A对；对于B选项，取，，则，B错；对于C选项，取，，则，C错；对于D选项，取，，则，D错.故选：A.7．D【分析】由已知条件可得，构造函数，，利用导数可得在上为增函数，从而可得，再由正余弦函数的单调性可得结论【详解】，，令，，，所以在上为增函数，∴，∵，均为锐角，∴， ∴， 故选：D.8．BC【分析】化简变形各个选项中的函数解析式，再求其最大值即可判断作答.【详解】对于A，，当且仅当，即时取“=”，即当时，，A不正确；对于B，，当且仅当，即时取“=”，即当时，，B正确；对于C，，当且仅当，即时取“=”，即当时，，C正确；对于D，依题意，由，都有意义，且得：，且，且，，，显然最大值为1，此时，，而使函数无意义，即不能取到1，D不正确.故选：BC9．ACD【解析】利用偶函数的定义可判断A；根据周期函数定义可判断B；利用可判断C；令，得可判断D.【详解】因为，，所以函数是偶函数，A正确；，所以的周期不是，B错误；由于，所以， 当时，，所以函数的最大值为，C正确；令，得，当时，，所以函数在上有无数个零点，D正确.故选：ACD.【点睛】本题主要考查余弦函数的性质，解题关键点是理解绝对值的意义和余弦函数的性质，需要根据奇偶性、周期、单调性和最值逐个去判断，考查运算能力、推理能力.10．BC【分析】令，则，再分析的奇偶性、周期性与单调性，即可判断；【详解】解：因为，令，则，对于A，因为是周期为的周期函数，关于轴对称，不是周期函数，所以不是周期函数，则也不是周期函数，故A错误；对于B，的定义域为，且，所以为偶函数，则，故为偶函数，故B正确；对于C，当时，，，所以单调递减，则单调递增，故C正确；对于D，当时，，则故的最小值不为，故D错误．故选：BC．11．BCD【分析】A.利用周期函数的定义判断；B.利用的关系判断；C.由时判断；D.由判断.【详解】A.，，故正确；B.，，故错误；C.当时，，则，在无单调性，故错误； D.，故错误；故选：BCD12．BD【分析】通过判断的值，判断A的正误；利用函数的导数判断函数的单调性，求解最大值，判断B的正误；求出函数的单调增区间判断C的正误；判断，判断D的正误．【详解】解：对于A，取，则，从而，此时不是奇函数，则A错误；对于B，当时，，当时，；当时，．所以在上单调递减，在上单调递增，所以的最小值为，故B正确；对于C，当时，，令，则，所以的递增区间为，则C错误；对于D，因为，所以的图象关于直线对称，则D正确；故选：BD.13．ABD【分析】由单调性和函数值分析周期，得出相邻的对称轴和对称中心，求得周期后得，然后得值，最后利用余弦函数性质确定减区间，对称轴，并利用图象变换判断各选项．【详解】由在区间上具有单调性可知，的最小正周期T满足，所以.又因为，所以，在同一个周期内且，故图像的一条对称轴为直线.又由，知图像的一个对称中心为，且所求得的对称轴与对称中心是相邻的，所以，得，即，故A正确；又因为图像的一个对称中心为，所以，所以，，由知，，则，由，，解得，，故B正确；令，，得，，故C错误；的图像向左平移个单位长度得的图像，故D正确.故选：ABD.14．BCD【分析】先将化简为，再结合余弦函数的性质判断4个选项即可.【详解】，故最小正周期为，A错误；，点是一个对称中心，B正确；向左平移个单位长度得到，关于轴对称，C正确；，单调递减，D正确.故选：BCD.15．ABC【分析】将变为结合指数函数的性质，判断A;构造函数，求导，利用其单调性结合图象判断x,y的范围，利用余弦函数单调性，判断B;利用正弦函数的单调性判断C，结合余弦函数的单调性，判断D.【详解】由题意，，得 ，，，∴，∴，A对；，令，即有，令，在上递减，在上递增，因为 ，∴，作出函数以及 大致图象如图：则，∴，结合图象则，∴，∴，B对；结合以上分析以及图象可得，∴，且 ，∴，C对；由C的分析可知，，在区间 上，函数 不是单调函数，即不成立，即不成立，故D错误；故选：ABC．【点睛】本题综合考查了有条件等式下三角函数值比较大小问题，设计指数函数性质，导数的应用以及三角函数的性质等，难度较大，解答时要注意构造函数，数形结合，综合分析，进行解答.16．ACD【分析】对于A，在中令，即可判断A；对于B，对两边求导，结合，即可得出在上单调递增，即可判断B.对于C，分别讨论和 ，再结合在上单调递增，上单调递减，即可判断C.对于D，先证明，则，再令，而由，所以，所以，即可判断D.【详解】对于A，在中令，则，所以，故A正确；对于B，当时，，对两边求导，则，所以时，，所以，令，，，所以在上单调递增，所以B错；对于C，由B知，在上单调递增，上单调递减，由知不可能均大于等于1，否则，则，这与条件矛盾，舍去.①若，则，满足条件，此时，；’②若，则，而，则，所以，而，所以，C正确；对于D，由在上单调递增，上单调递减，知，注意到，，，所以，若，则，则，所以()，这与矛盾，舍去.所以，在时，中，令，而由，所以，所以，故D正确.故选：ACD.17．【分析】常见的周期函数是三角函数，可以利用余弦型函数周期公式进行构造.【详解】因为函数的周期为，所以函数的周期为1.故答案为：.（答案不唯一）18．(1)当时， 的零点个数为0；当时， 的零点个数为1；(2). 【分析】（1）求导再对分三种情况讨论得解；（2）先证明满足题意；再讨论时，，综合即得解.(1)解：令．若，则，所以的零点个数为0；若，所以在上单调递增，又，所以的零点个数为1；若，所以在上单调递增，又，所以的零点个数为1．综上得，当时， 的零点个数为0；当时， 的零点个数为1.(2)解：由（1）知：若，故在上单调递增，所以，所以满足题意；若，存在唯，使得，且当时，，当时，，所以在上单调递减，在上单调递增．所以，化简得，又，所以，设，所以在上单调递减，所以，解得．综上所述，的取值范围为．