江苏省2022年高考数学模拟题分类汇编-函数的周期性、函数的对称性及函数的图像

这是一份江苏省2022年高考数学模拟题分类汇编-函数的周期性、函数的对称性及函数的图像，共32页。试卷主要包含了单选题，多选题，填空题，双空题等内容，欢迎下载使用。
江苏省2022年高考数学模拟题分类汇编-函数的周期性、函数的对称性及函数的图像

一、单选题
1．（2022·江苏泰州·模拟预测）已知定义在R上的奇函数满足，已知当时，，若恰有六个不相等的零点，则实数m的取值范围为（       ）
A． B．
C． D．
2．（2022·江苏江苏·二模）已知是定义域为R的偶函数，f(5.5)＝2，g(x)＝(x－1).若g(x＋1)是偶函数，则＝(       )
A．－3 B．－2 C．2 D．3
3．（2022·江苏淮安·模拟预测）已知函数，则的图象大致是（       ）
A． B．
C． D．
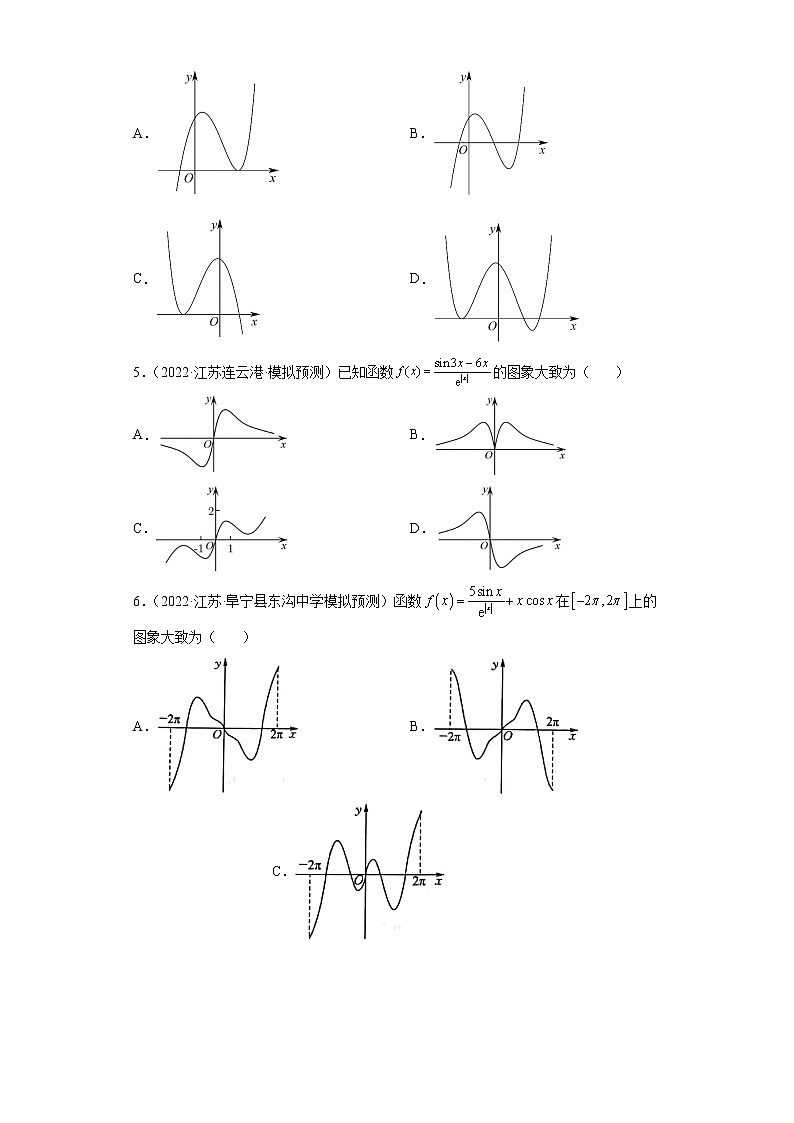
4．（2022·江苏盐城·三模）函数的大致图象是(       )
A． B．
C． D．
5．（2022·江苏连云港·模拟预测）已知函数的图象大致为（       ）
A． B．
C． D．
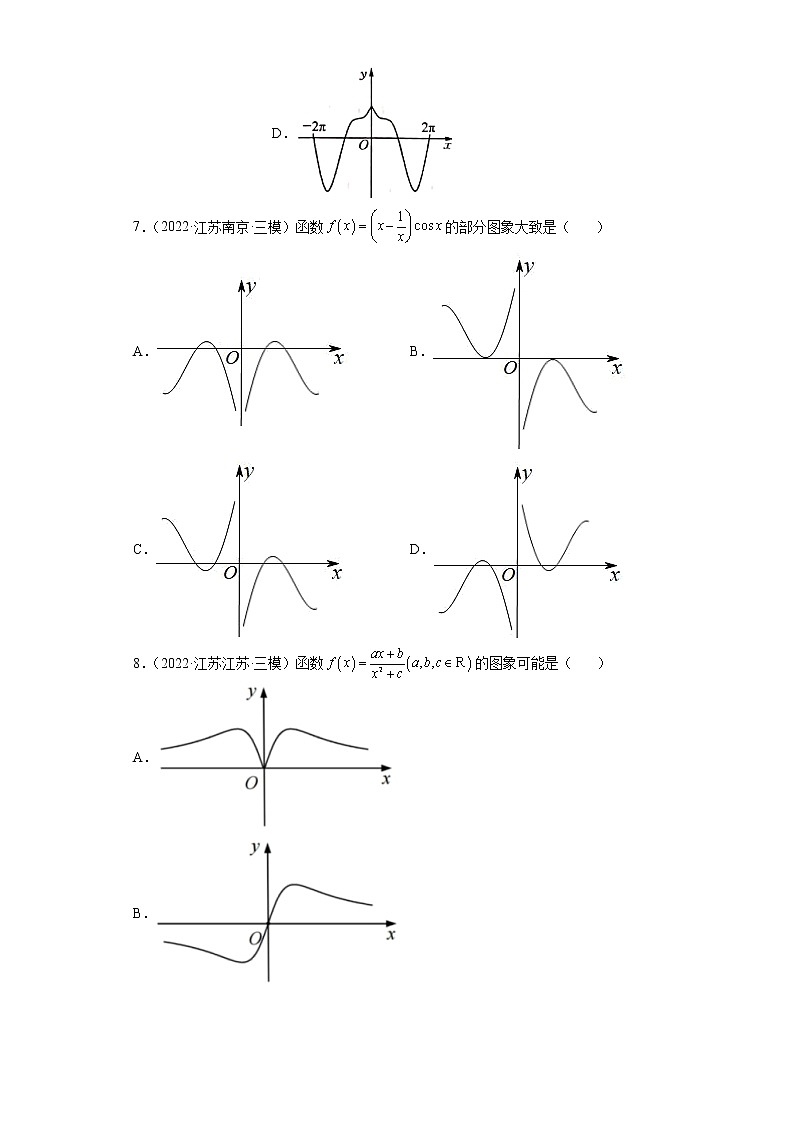
6．（2022·江苏·阜宁县东沟中学模拟预测）函数在上的图象大致为（       ）
A． B． C． D．
7．（2022·江苏南京·三模）函数的部分图象大致是（       ）
A． B．
C． D．
8．（2022·江苏江苏·三模）函数的图象可能是（       ）
A．
B．
C．
D．
9．（2022·江苏·南京市宁海中学二模）函数在其定义域上的图象大致是（       ）
A． B． C． D．
10．（2022·江苏·南京市第五高级中学一模）函数的图象大致为（       ）
A． B．
C． D．
11．（2022·江苏·模拟预测）已知函数y＝f（x）的部分图象如图所示，则函数f（x）的解析式最可能是（     ）

A．y＝xcosx B．y＝sinx－x2 C． D．y＝sinx＋x
12．（2022·江苏·南京市第五高级中学模拟预测）函数的图像可能是（       ）
A． B．
C． D．
13．（2022·江苏省滨海中学模拟预测）函数的大致图象为（       ）
A． B．
C． D．
14．（2022·江苏·扬中市第二高级中学模拟预测）函数的图象大致为(       )
A． B．
C． D．
15．（2022·江苏无锡·模拟预测）函数的图象大致为（       ）
A． B．
C． D．
16．（2022·江苏·徐州市第七中学模拟预测）我国著名数学家华罗庚说过：“数缺形时少直观，形少数时难入微，数形结合百般好，隔离分家万事休.”函数的部分图象大致为（       ）
A． B．
C． D．
17．（2022·江苏·南京市宁海中学模拟预测）函数的部分图象大致为（       ）
A． B． C． D．

二、多选题
18．（2022·江苏盐城·三模）已知函数为上的奇函数，为偶函数，下列说法正确的有（       ）
A．图象关于直线对称 B．
C．的最小正周期为4 D．对任意都有
19．（2022·江苏·华罗庚中学三模）是定义在上的函数，若是奇函数，是偶函数，函数，则（       ）
A．当时， B．当时，
C． D．
20．（2022·江苏常州·模拟预测）已知函数，则（       ）
A．函数的值域为
B．函数是一个偶函数，也是一个周期函数
C．直线是函数的一条对称轴
D．方程有且仅有一个实数根
21．（2022·江苏扬州·模拟预测）已知函数是定义在R上的奇函数，是偶函数，当，则下列说法中正确的有（       ）
A．函数关于直线对称
B．4是函数的周期
C．
D．方程恰有4不同的根
22．（2022·江苏·南京市宁海中学模拟预测）已知是定义在R上的偶函数，且对任意，有，当时，，则（       ）
A．是以2为周期的周期函数
B．点是函数的一个对称中心
C．
D．函数有3个零点
23．（2022·江苏泰州·模拟预测）已知定义在上的单调递增的函数满足：任意，有，，则（       ）
A．当时，
B．任意，
C．存在非零实数，使得任意，
D．存在非零实数，使得任意，
24．（2022·江苏·沭阳如东中学模拟预测）华人数学家李天岩和美国数学家约克给出了“混沌”的数学定义，由此发展的混沌理论在生物学､经济学和社会学领域都有重要作用.在混沌理论中，函数的周期点是一个关键概念，定义如下：设是定义在R上的函数，对于R，令，若存在正整数k使得，且当00时，x2是递增的，cosx在(0,)上递减，
则有g(x)在(0,)上单调递增，而，
所以存在使得，
中，排除C、D，
∵时，排除B，所以选A.
故选：A
【点睛】给定解析式，识别图象，可以从分析函数定义域、函数奇偶性、在特定区间上单调性及特殊值等方面入手.
15．C
【解析】分析函数的奇偶性及其在上的函数值符号，与的大小关系，由此可得出合适的选项.
【详解】函数的定义域为，，
所以，函数为奇函数，排除B选项；
当时，，则，排除D选项；
，，则，所以，函数在上不是减函数，排除A选项.
故选：C.
【点睛】思路点睛：函数图象的辨识可从以下方面入手：
（1）从函数的定义域，判断图象的左右位置；
（2）从函数的值域，判断图象的上下位置．
（3）从函数的单调性，判断图象的变化趋势；
（4）从函数的奇偶性，判断图象的对称性；
（5）函数的特征点，排除不合要求的图象.
16．C
【解析】首先排除函数的奇偶性，再判断时的函数值的正负.
【详解】，函数是奇函数，故排除AB，
当时，，，所以，故排除D.
故选：C
17．A
【解析】化简函数解析式，判断函数的对称性，再根据时，即可判断.
【详解】可得，
令，定义域为，且，
则为奇函数，关于原点对称，
是由向右平移2个单位所得，关于对称，故BC错误；
当时，，故D错误.
故选：A.
【点睛】本题考查函数图象的辨别，属于基础题.
18．ABD
【分析】由奇偶性知的对称中心为、对称轴为，进而推得，即可判断各选项的正误.
【详解】由的对称中心为，对称轴为，
则也关于直线对称且，A、D正确，
由A分析知：，故，
所以，
所以的周期为4，则，B正确；
但不能说明最小正周期为4，C错误；
故选：ABD
19．AD
【分析】先求出，对四个选项一一一验证：
对于A、B：利用代入法求解析式,即可判断；对于C:分别求出和，求出.即可判断;对于D：由，利用等比数列的求和公式即可求得.
【详解】因为是奇函数,是偶函数,则有，解得.
对于A：任取，则，所以.故A正确；
对于B：任取，则，所以.故B错误；
对于C:当x∈(2,3)时,有x-1∈(1,2),x-2∈(0,1).所以，则有，，故.故C错误;
对于D：由C的结论, ，则.故D正确.
故选：AD
20．ABD
【分析】利用函数的奇偶性、周期性分析判断A，B；利用对称的性质验证判断C；利用零点存在性定理分析判断D作答.
【详解】显然，，即函数是偶函数，
又，函数是周期函数，是它的一个周期，B正确；
当时，，的最小值为，最大值为，
即当时，的取值集合是，因是偶函数，则当时，的取值集合是，
因此，当时，的取值集合是，而是的周期，所以，的值域为，A正确；
因，，即函数图象上的点关于直线的对称点不在此函数图象上，C不正确；
因当时，恒有成立，而的值域为，方程在上无零点，
又当或时，的值与的值异号，即方程在、上都无零点，
令，，显然在单调递减，
而，，于是得存在唯一，使得，
因此，方程在上有唯一实根，则方程在上有唯一实根，又定义域为，
所以方程有且仅有一个实数根，D正确.
故选：ABD
【点睛】结论点睛：函数的定义域为D，，存在常数a使得，则函数图象关于直线对称.
21．ABD
【分析】根据奇偶性的定义，结合函数的对称性，即可判断A的正误；根据题意，结合函数的周期性，可判断B的正误；根据函数的周期性，结合解析式，即可判断C的正误；分别作出和的图象，即可判断D的正误，即可得答案.
【详解】对于A：因为是偶函数，
所以，即
所以关于对称，故A正确.
对于B：因为，
所以，
所以，即周期，故B正确
对于C：
所以，故C错误；
对于D：因为，且关于直线对称，
根据对称性可以作出上的图象，
又，根据对称性，可作出上的图象，
又的周期，
作出图象与图象，如下图所示：

所以与有4个交点，故D正确.
故选： ABD
22．BD
【分析】首先根据函数的对称性求出的周期和对称中心，然后求得.利用图象法即可判断D.
【详解】依题意，为偶函数，
且，有，即关于对称，
则
，
所以是周期为4的周期函数，故A错误；
因为的周期为4，关于对称，
所以是函数的一个对称中心，故B正确；
因为的周期为4，则，，
所以，故C错误；
作函数和的图象如下图所示，

由图可知，两个函数图象有3个交点，
所以函数有3个零点，故D正确.
故选：BD.
23．ABD
【分析】令可推导得，结合的值可知A正确；令可推导得，结合可推导知B正确；根据单调性可知C错误；当时，根据的对称中心及其在时的值域可确定时满足，知D正确.
【详解】对于A，令，则，即，
又，；
令得：，，，，
则由可知：当时，，A正确；
对于B，令，则，即，
，
由A的推导过程知：，，B正确；
对于C，为上的增函数，
当时，，则；当时，，则，
不存在非零实数，使得任意，，C错误；
对于D，当时，；
由，知：关于，成中心对称，则当时，为的对称中心；
当时，为上的增函数，，，，
；
由图象对称性可知：此时对任意，，D正确.
故选：ABD.
【点睛】关键点点睛：本题考查函数对称性的应用，解题关键是能够根据已知关系式确定的对称中心，同时采用赋值的方式确定所满足的其他关系式，从而结合对称性和其他函数关系式来确定所具有的其他性质.
24．AC
【分析】根据题意中周期点定义，分别求出当、、、时的函数周期，进而得出结果.
【详解】A：时，，周期为1，故A正确；
B：时，，
所以不是的周期点.故B错误；
C：时，，周期为1，故C正确；
D：时，，不是周期为1的周期点，故D错误.
故选：AC.
25．CD
【分析】通过举反例判断选项AB的真假，证明选项CD正确即得解.
【详解】解：A. 如由于函数是增函数，所以不是极值点，所以该选项错误；
B. 如是偶函数，但是不是奇函数，所以该选项错误；
C. 是周期为的周期函数，所以，所以也是周期为的周期函数，所以该选项正确；
D. 的图象关于直线对称，所以，所以，所以的图象关于点中心对称，所以该选项正确.
故选：CD
26．BCD
【分析】利用对称性定义推理判断A；由与在上单调性判断B；借助导数求出在周期长的区间上的最大值判断C；由在周期长的区间上的最大最小值判断D作答.
【详解】对于A，因，则的图象关于对称，不关于对称，A错误；
对于B，因与在上都是增函数，则在上是增函数，B正确；
对于C，因，即是奇函数，
又与的最小正周期分别为与，则的正周期为，
当时，，令，得，即，
当时，，当时，，则在上递增，在上递减，
因此，在上的最大值为，由是奇函数得在上的最大值为，
由的正周期为，则在R上的最大值为，C正确；
对于D，由选项C得，，，，
又，则，
所以当时，，D正确．
故选：BCD
27．ABD
【分析】由题设且，可得，代入解析式，结合已知条件即可判断选项的正误.
【详解】由题设，，且，
所以，整理得，
故，可得，故，
又，即，A正确；有3个零点，B正确；
由，则，所以关于对称，C错误；
，D正确.
故选：ABD
28．BC
【分析】验证可判断A；求导分析导函数正负，可判断B；令，求导分析单调性，可得，分析可判断C；由可判断D
【详解】选项A，，
故函数（x）的图象不关于直线对称，错误；
选项B，
令
故在单调递减，故
即，故在（0，π）上单调递减，正确；
选项C，，故
令
故在单调递减，故
即，正确；
选项D，由选项C，可得，故，错误
故选：BC
29．AD
【分析】求f(x)的导数，研究其导数的单调性和正负，从而判断f(x)的单调性，从而选出符合的图象．
【详解】，
令，，
在单调递减，且，
若，
则时，单调递增，
时，单调递减，
∴，，，
∴在各有一个零点，设，
时，单调递减，
时，单调递增，
时，单调递减，故D满足条件；
若，则A满足条件．
故选：AD．
30．3
【分析】先由函数的图像关于直线对称，得到函数是偶函数，则有；
又令代入，求得函数的周期为，利用函数周期化简即可求值.
【详解】因为函数的图像关于直线对称，所以函数的图像关于直线对称，即函数是偶函数，则有；
因为对任意，都有，
令，得，
所以对任意，都有，即函数的周期为，
则，
故答案为：.
31．
【分析】首先得到函数的周期，再利用函数的周期和奇偶性，化简求值.
【详解】，，且函数是奇函数，所以化简
，
，，
.
故答案为：-2
【点睛】关键点点睛：本题的关键是利用函数的周期性和奇函数的性质化简.
32．1
【分析】根据题意求出，从而列出方程，求出.
【详解】∵，函数y=的图象与的图象关于直线y=x对称
∴，
∴
∴
∴．
故答案为：1
33．（答案不唯一）
【分析】根据满足的条件写出一个函数即可.
【详解】由条件①②③可知函数对称轴为，定义域为R的奇函数，可写出满足条件的函数.
故答案为：（答案不唯一）
34．##0.25
【分析】根据题设条件画出函数的图象，结合图象可求实数的最大值.
【详解】因为，故的图象关于中心对称
当时，，
故的图象如图所示：

结合图象可得：只需当时，即可，
即，故，
故答案为：.
35．##
【分析】由题设可得，根据对数性质判断的符号，结合已知解析式求函数即可.
【详解】由题设，，又，
所以.
故答案为：
36．
【分析】将题设转化为函数的图像和的图象有两个交点，求出直线和相切时的值以及直线过点时的值，结合图象即可求解.
【详解】
由，解得，
又关于直线的对称直线为，
则题设等价于函数的图像和的图象有两个交点.
易得等价于，
画出和的图象，设直线和相切，
由，解得或（舍），
又当直线过点时，，
结合图象可知，当时，
函数的图像和的图象有两个交点.
故答案为：.
37．          ##2.5
【分析】第一空先求出函数在上的解析式，结合奇函数画出的图像，再由得到，
进而得到函数在上的图像，即可求得值域；
第二空画出将零点转化为的交点，再画出的图像即可求解.
【详解】由当时，，可得当时，，当时，，
又是奇函数，可得函数图像关于原点对称.又当时，即，即，
即函数右移两个单位，函数值变为原来的2倍，由此可得函数在上的图像如图所示：

结合图像可知在区间上的值域为；，即，即的交点，
画出的图像，由图像可知4个交点的横坐标依次为，又均是奇函数，故，
故.
故答案为：；.