四川省2022年各地区中考数学真题按题型分层分类汇编-08解答题（提升题）

这是一份四川省2022年各地区中考数学真题按题型分层分类汇编-08解答题（提升题），共46页。试卷主要包含了，B两点，分别连接OA，OB，，B两点，，与y轴交于点C等内容，欢迎下载使用。
四川省2022年各地区中考数学真题按题型分层分类汇编-08解答题（提升题）
一．反比例函数与一次函数的交点问题（共1小题）
1．（2022•绵阳）如图，一次函数y＝k1x+b与反比例函数y＝在第一象限交于M（2，8）、N两点，NA垂直x轴于点A，O为坐标原点，四边形OANM的面积为38．
（1）求反比例函数及一次函数的解析式；
（2）点P是反比例函数第三象限内的图象上一动点，请简要描述使△PMN的面积最小时点P的位置（不需证明），并求出点P的坐标和△PMN面积的最小值．

二．反比例函数综合题（共2小题）
2．（2022•达州）如图，一次函数y＝x+1与反比例函数y＝的图象相交于A（m，2），B两点，分别连接OA，OB．
（1）求这个反比例函数的表达式；
（2）求△AOB的面积；
（3）在平面内是否存在一点P，使以点O，B，A，P为顶点的四边形为平行四边形？若存在，请直接写出点P的坐标；若不存在，请说明理由．

3．（2022•成都）如图，在平面直角坐标系xOy中，一次函数y＝﹣2x+6的图象与反比例函数y＝的图象相交于A（a，4），B两点．
（1）求反比例函数的表达式及点B的坐标；
（2）过点A作直线AC，交反比例函数图象于另一点C，连接BC，当线段AC被y轴分成长度比为1：2的两部分时，求BC的长；
（3）我们把有两个内角是直角，且一条对角线垂直平分另一条对角线的四边形称为“完美筝形”．设P是第三象限内的反比例函数图象上一点，Q是平面内一点，当四边形ABPQ是完美筝形时，求P，Q两点的坐标．

三．二次函数综合题（共5小题）
4．（2022•内江）如图，抛物线y＝ax2+bx+c与x轴交于A（﹣4，0），B（2，0），与y轴交于点C（0，2）．
（1）求这条抛物线所对应的函数的表达式；
（2）若点D为该抛物线上的一个动点，且在直线AC上方，求点D到直线AC的距离的最大值及此时点D的坐标；
（3）点P为抛物线上一点，连接CP，直线CP把四边形CBPA的面积分为1：5两部分，求点P的坐标．


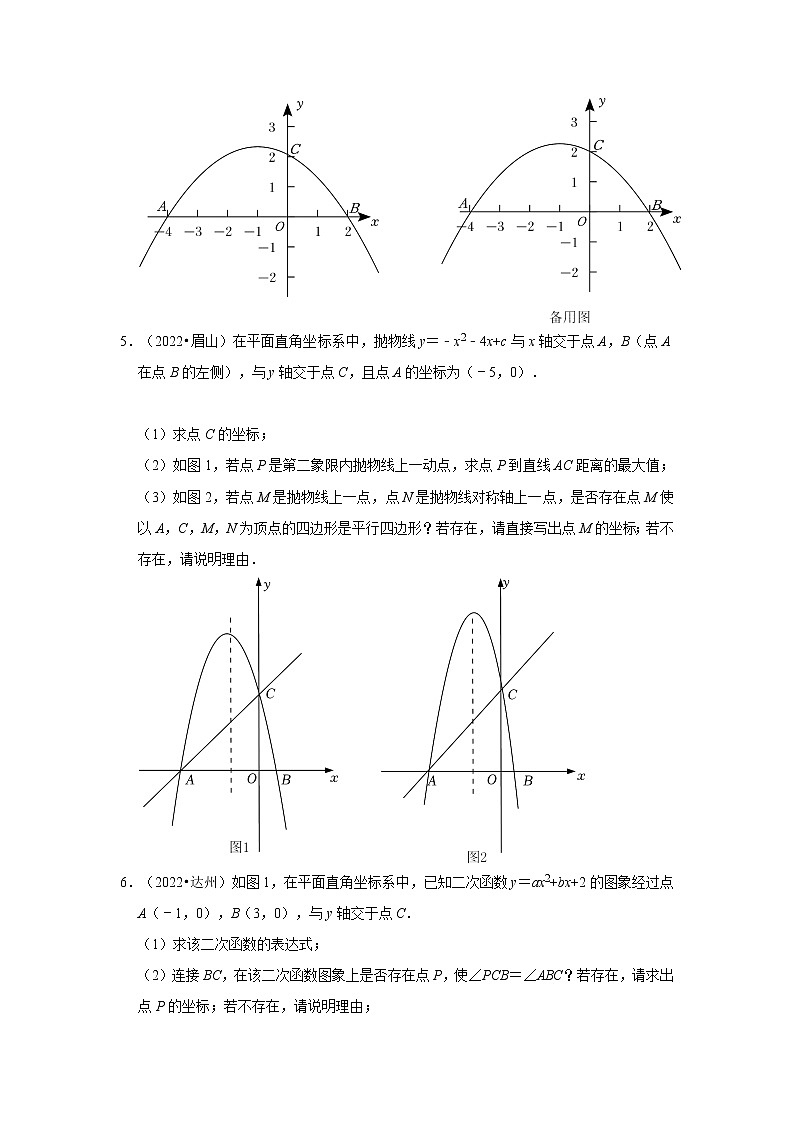
5．（2022•眉山）在平面直角坐标系中，抛物线y＝﹣x2﹣4x+c与x轴交于点A，B（点A在点B的左侧），与y轴交于点C，且点A的坐标为（﹣5，0）．

（1）求点C的坐标；
（2）如图1，若点P是第二象限内抛物线上一动点，求点P到直线AC距离的最大值；
（3）如图2，若点M是抛物线上一点，点N是抛物线对称轴上一点，是否存在点M使以A，C，M，N为顶点的四边形是平行四边形？若存在，请直接写出点M的坐标；若不存在，请说明理由．

6．（2022•达州）如图1，在平面直角坐标系中，已知二次函数y＝ax2+bx+2的图象经过点A（﹣1，0），B（3，0），与y轴交于点C．
（1）求该二次函数的表达式；
（2）连接BC，在该二次函数图象上是否存在点P，使∠PCB＝∠ABC？若存在，请求出点P的坐标；若不存在，请说明理由；
（3）如图2，直线l为该二次函数图象的对称轴，交x轴于点E．若点Q为x轴上方二次函数图象上一动点，过点Q作直线AQ，BQ分别交直线l于点M，N，在点Q的运动过程中，EM+EN的值是否为定值？若是，请求出该定值；若不是，请说明理由．

7．（2022•凉山州）在平面直角坐标系xOy中，已知抛物线y＝﹣x2+bx+c经过点A（﹣1，0）和点B（0，3），顶点为C，点D在其对称轴上，且位于点C下方，将线段DC绕点D按顺时针方向旋转90°，点C落在抛物线上的点P处．
（1）求抛物线的解析式；
（2）求点P的坐标；
（3）将抛物线平移，使其顶点落在原点O，这时点P落在点E的位置，在y轴上是否存在点M，使得MP+ME的值最小，若存在，求出点M的坐标；若不存在，请说明理由．

8．（2022•自贡）已知二次函数y＝ax2+bx+c（a≠0）．
（1）若a＝﹣1，且函数图象经过（0，3），（2，﹣5）两点，求此二次函数的解析式，直接写出抛物线与x轴交点及顶点坐标；
（2）在图①中画出（1）中函数的大致图象，并根据图象写出函数值y≥3时自变量x的取值范围；
（3）若a+b+c＝0且a＞b＞c，一元二次方程ax2+bx+c＝0两根之差等于a﹣c，函数图象经过P（﹣c，y1），Q（1+3c，y2）两点，试比较y1、y2的大小．


四．四边形综合题（共1小题）
9．（2022•绵阳）如图，平行四边形ABCD中，DB＝2，AB＝4，AD＝2，动点E、F同时从A点出发，点E沿着A→D→B的路线匀速运动，点F沿着A→B→D的路线匀速运动，当点E，F相遇时停止运动．
（1）如图1，设点E的速度为1个单位每秒，点F的速度为4个单位每秒，当运动时间为秒时，设CE与DF交于点P，求线段EP与CP长度的比值；
（2）如图2，设点E的速度为1个单位每秒，点F的速度为个单位每秒，运动时间为x秒，△AEF的面积为y，求y关于x的函数解析式，并指出当x为何值时，y的值最大，最大值为多少？
（3）如图3，H在线段AB上且AH＝HB，M为DF的中点，当点E、F分别在线段AD、AB上运动时，探究点E、F在什么位置能使EM＝HM，并说明理由．


五．切线的判定与性质（共1小题）
10．（2022•德阳）如图，AB是⊙O的直径，CD是⊙O的弦，AB⊥CD，垂足是点H，过点C作直线分别与AB，AD的延长线交于点E，F，且∠ECD＝2∠BAD．
（1）求证：CF是⊙O的切线；
（2）如果AB＝10，CD＝6，
①求AE的长；
②求△AEF的面积．

六．圆的综合题（共5小题）
11．（2022•绵阳）如图，AB为⊙O的直径，C为圆上的一点，D为劣弧的中点，过点D作⊙O的切线与AC的延长线交于点P，与AB的延长线交于点F，AD与BC交于点E．
（1）求证：BC∥PF；
（2）若⊙O的半径为，DE＝1，求AE的长度；
（3）在（2）的条件下，求△DCP的面积．

12．（2022•达州）如图，在Rt△ABC中，∠C＝90°，点O为AB边上一点，以OA为半径的⊙O与BC相切于点D，分别交AB，AC边于点E，F．
（1）求证：AD平分∠BAC；
（2）若BD＝3，tan∠CAD＝，求⊙O的半径．

13．（2022•凉山州）如图，已知半径为5的⊙M经过x轴上一点C，与y轴交于A、B两点，连接AM、AC，AC平分∠OAM，AO+CO＝6．
（1）判断⊙M与x轴的位置关系，并说明理由；
（2）求AB的长；
（3）连接BM并延长交⊙M于点D，连接CD，求直线CD的解析式．

14．（2022•成都）如图，在Rt△ABC中，∠ACB＝90°，以BC为直径作⊙O，交AB边于点D，在上取一点E，使＝，连接DE，作射线CE交AB边于点F．
（1）求证：∠A＝∠ACF；
（2）若AC＝8，cos∠ACF＝，求BF及DE的长．

15．（2022•泸州）如图，点C在以AB为直径的⊙O上，CD平分∠ACB交⊙O于点D，交AB于点E，过点D作⊙O的切线交CO的延长线于点F．
（1）求证：FD∥AB；
（2）若AC＝2，BC＝，求FD的长．

七．几何变换综合题（共1小题）
16．（2022•广元）在Rt△ABC中，AC＝BC，将线段CA绕点C旋转α（0°＜α＜90°），得到线段CD，连接AD、BD．
（1）如图1，将线段CA绕点C逆时针旋转α，则∠ADB的度数为 　 　；
（2）将线段CA绕点C顺时针旋转α时
①在图2中依题意补全图形，并求∠ADB的度数；
②若∠BCD的平分线CE交BD于点F，交DA的延长线于点E，连结BE．用等式表示线段AD、CE、BE之间的数量关系，并证明．



四川省2022年各地区中考数学真题按题型分层分类汇编-08解答题（提升题）
参考答案与试题解析
一．反比例函数与一次函数的交点问题（共1小题）
1．（2022•绵阳）如图，一次函数y＝k1x+b与反比例函数y＝在第一象限交于M（2，8）、N两点，NA垂直x轴于点A，O为坐标原点，四边形OANM的面积为38．
（1）求反比例函数及一次函数的解析式；
（2）点P是反比例函数第三象限内的图象上一动点，请简要描述使△PMN的面积最小时点P的位置（不需证明），并求出点P的坐标和△PMN面积的最小值．

【解答】解：（1）∵反比例函数y＝过点M（2，8），
∴k2＝2×8＝16，
∴反比例函数的解析式为y＝，
设N（m，），
∵M（2，8），
∴S△OMB＝＝8，
∵四边形OANM的面积为38，
∴四边形ABMN的面积为30，
∴（8+）•（m﹣2）＝30，
解得m1＝8，m2＝﹣（舍去），
∴N（8，2），
∵一次函数y＝k1x+b的图象经过点M、N，
∴，解得，
∴一次函数的解析式为y＝﹣x+10；
（2）与直线MN平行，且在第三象限与反比例函数y＝有唯一公共点P时，△PMN的面积最小，
设与直线MN平行的直线的关系式为y＝﹣x+n，当与y＝在第三象限有唯一公共点时，
有方程﹣x+n＝（x＜0）唯一解，
即x2﹣nx+16＝0有两个相等的实数根，
∴n2﹣4×1×16＝0，
解得n＝﹣8或x＝8（舍去），
∴与直线MN平行的直线的关系式为y＝﹣x﹣8，
∴方程﹣x﹣8＝的解为x＝﹣4，
经检验，x＝﹣4是原方程的解，
当x＝﹣4时，y＝＝﹣4，
∴点P（﹣4，﹣4），
如图，过点P作AN的垂线，交NA的延长线于点Q，交y轴于点D，延长MB交PQ于点C，由题意得，
PD＝4，DQ＝8，CD＝2，MC＝8+4＝12，NQ＝2+4＝6，
∴S△PMN＝S△MPC+S梯形MCQN﹣S△PNQ
＝×6×12+（12+6）×6﹣×12×6
＝36+54﹣36
＝54，
答：点P（﹣4，﹣4），△PMN面积的最小值为54．

二．反比例函数综合题（共2小题）
2．（2022•达州）如图，一次函数y＝x+1与反比例函数y＝的图象相交于A（m，2），B两点，分别连接OA，OB．
（1）求这个反比例函数的表达式；
（2）求△AOB的面积；
（3）在平面内是否存在一点P，使以点O，B，A，P为顶点的四边形为平行四边形？若存在，请直接写出点P的坐标；若不存在，请说明理由．

【解答】解：（1）∵一次函数y＝x+1经过点A（m，2），
∴m+1＝2，
∴m＝1，
∴A（1，2），
∵反比例函数y＝经过点（1，2），
∴k＝2，
∴反比例函数的解析式为y＝；

（2）由题意，得，
解得或，
∴B（﹣2，﹣1），
∵C（0，1），
∴S△AOB＝S△AOC+S△BOC＝×1×2+×1×1＝1.5；

（3）有三种情形，如图所示，满足条件的点P的坐标为（﹣3，﹣3）或（﹣1，1）或（3，3）．

3．（2022•成都）如图，在平面直角坐标系xOy中，一次函数y＝﹣2x+6的图象与反比例函数y＝的图象相交于A（a，4），B两点．
（1）求反比例函数的表达式及点B的坐标；
（2）过点A作直线AC，交反比例函数图象于另一点C，连接BC，当线段AC被y轴分成长度比为1：2的两部分时，求BC的长；
（3）我们把有两个内角是直角，且一条对角线垂直平分另一条对角线的四边形称为“完美筝形”．设P是第三象限内的反比例函数图象上一点，Q是平面内一点，当四边形ABPQ是完美筝形时，求P，Q两点的坐标．

【解答】解：（1）∵一次函数y＝﹣2x+6的图象过点A，
∴4＝﹣2a+6，
∴a＝1，
∴点A（1，4），
∵反比例函数y＝的图象过点A（1，4），
∴k＝1×4＝4；
∴反比例函数的解析式为：y＝，
联立方程组可得：，
解得：，，
∴点B（2，2）；
（2）如图，过点A作AE⊥y轴于E，过点C作CF⊥y轴于F，

∴AE∥CF，
∴△AEH∽△CFH，
∴，
当＝时，则CF＝2AE＝2，
∴点C（﹣2，﹣2），
∴BC＝＝4，
当＝2时，则CF＝AE＝，
∴点C（﹣，﹣8），
∴BC＝＝，
综上所述：BC的长为4或；
（3）如图，当∠AQP＝∠ABP＝90°时，设直线AB与y轴交于点E，过点B作BF⊥y轴于F，设BP与y轴的交点为N，连接BQ，AP交于点H，

∵直线y＝﹣2x+6与y轴交于点E，
∴点E（0，6），
∵点B（2，2），
∴BF＝OF＝2，
∴EF＝4，
∵∠ABP＝90°，
∴∠ABF+∠FBN＝90°＝∠ABF+∠BEF，
∴∠BEF＝∠FBN，
又∵∠EFB＝∠ABN＝90°，
∴△EBF∽△BNF，
∴，
∴FN＝＝1，
∴点N（0，1），
∴直线BN的解析式为：y＝x+1，
联立方程组得：，
解得：，，
∴点P（﹣4，﹣1），
∴直线AP的解析式为：y＝x+3，
∵AP垂直平分BQ，
∴设BQ的解析式为y＝﹣x+4，
∴x+3＝﹣x+4，
∴x＝，
∴点H（，），
∵点H是BQ的中点，点B（2，2），
∴点Q（﹣1，5）．
三．二次函数综合题（共5小题）
4．（2022•内江）如图，抛物线y＝ax2+bx+c与x轴交于A（﹣4，0），B（2，0），与y轴交于点C（0，2）．
（1）求这条抛物线所对应的函数的表达式；
（2）若点D为该抛物线上的一个动点，且在直线AC上方，求点D到直线AC的距离的最大值及此时点D的坐标；
（3）点P为抛物线上一点，连接CP，直线CP把四边形CBPA的面积分为1：5两部分，求点P的坐标．


【解答】解：（1）∵抛物线y＝ax2+bx+c与x轴交于A（﹣4，0），B（2，0），与y轴交于点C（0，2）．
∴，
解得：，
∴抛物线的解析式为y＝﹣x2﹣x+2；

（2）过点D作DH⊥AB于H，交直线AC于点G，过点D作DE⊥AC于E，如图．

设直线AC的解析式为y＝kx+t，
则，
解得：，
∴直线AC的解析式为y＝x+2．
设点D的横坐标为m，则点G的横坐标也为m，
∴DH＝﹣m2﹣m+2，GH＝m+2
∴DG＝﹣m2﹣m+2﹣m﹣2＝﹣m2﹣m，
∵DE⊥AC，DH⊥AB，
∴∠EDG+DGE＝AGH+∠CAO＝90°，
∵∠DGE＝∠AGH，
∴∠EDG＝∠CAO，
∴cos∠EDG＝cos∠CAO＝＝，
∴，
∴DE＝DG＝（﹣m2﹣m）＝﹣（m2+4m）＝﹣（m+2）2+，
∴当m＝﹣2时，点D到直线AC的距离取得最大值．
此时yD＝﹣×（﹣2）2﹣×（﹣2）+2＝2，
即点D的坐标为（﹣2，2）；

（3）如图，设直线CP交x轴于点E，

直线CP把四边形CBPA的面积分为1：5两部分，
又∵S△PCB：S△PCA＝EB×（yC﹣yP）：AE×（yC﹣yP）＝BE：AE，
则BE：AE＝1：5或5：1
则AE＝5或1，
即点E的坐标为（1，0）或（﹣3，0），
将点E的坐标代入直线CP的表达式：y＝nx+2，
解得：n＝﹣2或，
故直线CP的表达式为：y＝﹣2x+2或y＝x+2，
联立方程组或，
解得：x＝6或﹣（不合题意值已舍去），
故点P的坐标为（6，﹣10）或（﹣，﹣）．
5．（2022•眉山）在平面直角坐标系中，抛物线y＝﹣x2﹣4x+c与x轴交于点A，B（点A在点B的左侧），与y轴交于点C，且点A的坐标为（﹣5，0）．

（1）求点C的坐标；
（2）如图1，若点P是第二象限内抛物线上一动点，求点P到直线AC距离的最大值；
（3）如图2，若点M是抛物线上一点，点N是抛物线对称轴上一点，是否存在点M使以A，C，M，N为顶点的四边形是平行四边形？若存在，请直接写出点M的坐标；若不存在，请说明理由．

【解答】解：（1）∵点A（﹣5，0）在抛物线y＝﹣x2﹣4x+c的图象上，
∴0＝﹣52﹣4×5+c
∴c＝5，
∴点C的坐标为（0，5）；
（2）过P作PE⊥AC于点E，过点P作PF⊥x轴交AC于点H，如图1：
∵A（﹣5，0），C（0，5）
∴OA＝OC，
∴△AOC是等腰直角三角形，
∴∠CAO＝45°，
∵PF⊥x轴，
∴∠AHF＝45°＝∠PHE，
∴△PHE是等腰直角三角形，
∴，
∴当PH最大时，PE最大，
设直线AC解析式为y＝kx+5，
将A（﹣5，0）代入得0＝5k+5，
∴k＝1，
∴直线AC解析式为y＝x+5，
设P（m，﹣m2﹣4m+5），（﹣5＜m＜0），则H（m，m+5），
∴，
∵a＝﹣1＜0，
∴当时，PH最大为，
∴此时PE最大为，即点P到直线AC的距离值最大；
（3）存在，理由如下：
∵y＝﹣x2﹣4x+5＝﹣（x+2）2+9，
∴抛物线的对称轴为直线x＝﹣2，
设点N的坐标为（﹣2，m），点M的坐标为（x，﹣x2﹣4x+5），
分三种情况：①当AC为平行四边形对角线时，
，
解得，
∴点M的坐标为（﹣3，8）；
②当AM为平行四边形对角线时，
，
解得，
∴点M的坐标为（3，﹣16）；
③当AN为平行四边形对角线时，
，
解得，
∴点M的坐标为（﹣7，﹣16）；
综上，点M的坐标为：（﹣3，8）或（3，﹣16）或（﹣7，﹣16）．

6．（2022•达州）如图1，在平面直角坐标系中，已知二次函数y＝ax2+bx+2的图象经过点A（﹣1，0），B（3，0），与y轴交于点C．
（1）求该二次函数的表达式；
（2）连接BC，在该二次函数图象上是否存在点P，使∠PCB＝∠ABC？若存在，请求出点P的坐标；若不存在，请说明理由；
（3）如图2，直线l为该二次函数图象的对称轴，交x轴于点E．若点Q为x轴上方二次函数图象上一动点，过点Q作直线AQ，BQ分别交直线l于点M，N，在点Q的运动过程中，EM+EN的值是否为定值？若是，请求出该定值；若不是，请说明理由．

【解答】解：（1）∵抛物线y＝ax2+bx+2经过点A（﹣1，0），B（3，0），
∴，
解得：
∴该二次函数的表达式为y＝x2+x+2；
（2）存在，理由如下：
如图1，当点P在BC上方时，
∵∠PCB＝∠ABC，
∴CP∥AB，即CP∥x轴，
∴点P与点C关于抛物线对称轴对称，
∵y＝x2+x+2，
∴抛物线对称轴为直线x＝﹣＝1，
∵C（0，2），
∴P（2，2）；
当点P在BC下方时，设CP交x轴于点D（m，0），
则OD＝m，DB＝3﹣m，
∵∠PCB＝∠ABC，
∴CD＝BD＝3﹣m，
在Rt△COD中，OC2+OD2＝CD2，
∴22+m2＝（3﹣m）2，
解得：m＝，
∴D（，0），
设直线CD的解析式为y＝kx+d，则，
解得：，
∴直线CD的解析式为y＝x+2，
联立，得，
解得：（舍去），，
∴P（，﹣），
综上所述，点P的坐标为（2，2）或（，﹣）；
（3）由（2）知：抛物线y＝x2+x+2的对称轴为直线x＝1，
∴E（1，0），
设Q（t，t2+t+2），且﹣1＜t＜3，
设直线AQ的解析式为y＝ex+f，则，
解得：，
∴直线AQ的解析式为y＝（t+2）x﹣t+2，
当x＝1时，y＝﹣t+4，
∴M（1，﹣t+4），
同理可得直线BQ的解析式为y＝（﹣t﹣）x+2t+2，
当x＝1时，y＝t+，
∴N（1，t+），
∴EM＝﹣t+4，EN＝t+，
∴EM+EN＝﹣t+4+t+＝，
故EM+EN的值为定值．

7．（2022•凉山州）在平面直角坐标系xOy中，已知抛物线y＝﹣x2+bx+c经过点A（﹣1，0）和点B（0，3），顶点为C，点D在其对称轴上，且位于点C下方，将线段DC绕点D按顺时针方向旋转90°，点C落在抛物线上的点P处．
（1）求抛物线的解析式；
（2）求点P的坐标；
（3）将抛物线平移，使其顶点落在原点O，这时点P落在点E的位置，在y轴上是否存在点M，使得MP+ME的值最小，若存在，求出点M的坐标；若不存在，请说明理由．

【解答】解：（1）把A（﹣1，0）和点B（0，3）代入y＝﹣x2+bx+c，
得，
解得：，
∴抛物线解析式为y＝﹣x2+2x+3；

（2）∵y＝﹣（x﹣1）2+4，
∴C（1，4），抛物线的对称轴为直线x＝1，
如图，设CD＝t，则D（1，4﹣t），

∵线段DC绕点D按顺时针方向旋转90°，点C落在抛物线上的点P处，
∴∠PDC＝90°，DP＝DC＝t，
∴P（1+t，4﹣t），
把P（1+t，4﹣t）代入y＝﹣x2+2x+3得：
﹣（1+t）2+2（1+t）+3＝4﹣t，
整理得t2﹣t＝0，
解得：t1＝0（舍去），t2＝1，
∴P（2，3）；

（3）∵P点坐标为（2，3），顶点C坐标为（1，4），将抛物线平移，使其顶点落在原点O，这时点P落在点E的位置，
∴E点坐标为（1，﹣1），
∴点E关于y轴的对称点F（﹣1，﹣1），
连接PF交y轴于M，则MP+ME＝MP+MF＝PF的值最小，

设直线PF的解析式为y＝kx+n，
∴，
解得：，
∴直线PF的解析式为y＝x+，
∴点M的坐标为（0，）．
8．（2022•自贡）已知二次函数y＝ax2+bx+c（a≠0）．
（1）若a＝﹣1，且函数图象经过（0，3），（2，﹣5）两点，求此二次函数的解析式，直接写出抛物线与x轴交点及顶点坐标；
（2）在图①中画出（1）中函数的大致图象，并根据图象写出函数值y≥3时自变量x的取值范围；
（3）若a+b+c＝0且a＞b＞c，一元二次方程ax2+bx+c＝0两根之差等于a﹣c，函数图象经过P（﹣c，y1），Q（1+3c，y2）两点，试比较y1、y2的大小．


【解答】解：（1）由题意可得：，
解得：，
∴抛物线的解析式为：y＝﹣x2﹣2x+3＝﹣（x+1）2+4，
∴顶点坐标为（﹣1，4），
当y＝0时，则0＝﹣x2﹣2x+3，
∴x1＝1，x2＝﹣3，
∴抛物线与x轴的交点坐标为（1，0），（﹣3，0）；
（2）如图，

当y＝3时，3＝﹣x2﹣2x+3，
∴x1＝0，x2＝﹣2，
由图象可得：当﹣2≤x≤0时，y≥3；
（3）∵a+b+c＝0且a＞b＞c，
∴a＞0，c＜0，b＝﹣a﹣c，一元二次方程ax2+bx+c＝0必有一根为x＝1，
∵一元二次方程ax2+bx+c＝0两根之差等于a﹣c，
∴方程的另一个根为1+c﹣a，
∴抛物线y＝ax2+bx+c的对称轴为：直线x＝1+，
∴﹣＝1+，
∴a+c＝﹣a2+ac+2a，
∴（a﹣1）（a﹣c）＝0，
∵a＞c，
∴a＝1，P（﹣c，y1），Q（1+3c，y2），
∴b＝﹣1﹣c，
∴抛物线解析式为：y＝x2﹣（1+c）x+c，
∴当x＝﹣c时，则y1＝（﹣c）2﹣（1+c）（﹣c）+c＝2c2+c﹣，
当x＝1+3c时，则y2＝（1+3c）2﹣（1+c）（1+3c）+c＝6c2+3c，
∴y2﹣y1＝（6c2+3c）﹣（2c2+c﹣）＝4（c+）2﹣，
∵b＞c，
∴﹣1﹣c＞c，
∴c＜﹣，
∴4（c+）2﹣＞0，
∴y2＞y1．
四．四边形综合题（共1小题）
9．（2022•绵阳）如图，平行四边形ABCD中，DB＝2，AB＝4，AD＝2，动点E、F同时从A点出发，点E沿着A→D→B的路线匀速运动，点F沿着A→B→D的路线匀速运动，当点E，F相遇时停止运动．
（1）如图1，设点E的速度为1个单位每秒，点F的速度为4个单位每秒，当运动时间为秒时，设CE与DF交于点P，求线段EP与CP长度的比值；
（2）如图2，设点E的速度为1个单位每秒，点F的速度为个单位每秒，运动时间为x秒，△AEF的面积为y，求y关于x的函数解析式，并指出当x为何值时，y的值最大，最大值为多少？
（3）如图3，H在线段AB上且AH＝HB，M为DF的中点，当点E、F分别在线段AD、AB上运动时，探究点E、F在什么位置能使EM＝HM，并说明理由．


【解答】解：（1）延长DF交CB的延长线于G，
∵平行四边形ABCD中，
∴CG∥AD，
∴∠A＝∠GBF，
∴△AFD∽△BFG，
∴＝，
∵运动时间为秒，
∴AF＝，
∵AB＝4，
∴BF＝，
∵AD＝2，
∴BG＝1，
∴CG＝3，
∵AD∥CG，
∴＝，
∵AE＝，
∴ED＝，
∴＝；
（2）当0≤x≤2时，E点在AD上，F点在AB上，
由题意可知，AE＝x，AF＝x，
∵DB＝2，AB＝4，AD＝2，
∴△ABD是直角三角形，且∠A＝60°，
过点E作EH⊥AB交于H，
∴EH＝AE•sin60°＝x，
∴y＝×AF×EH＝×x×x＝x2；
此时当x＝2时，y有最大值3；
当2≤x≤时，E点在BD上，F点在AB上，
过点E作EN⊥AB交于N，过点D作DM⊥AB交于M，
∵AD+DE＝x，AD＝2，
∴DE＝x﹣2，
∵BD＝2，
∴BE＝2﹣x+2，
在Rt△ABD中，DM＝，
∵EN∥DM，
∴＝，
∴＝，
∴EN＝1+﹣x，
∴y＝×AF×EN＝×（x）×（1+﹣x）＝﹣x2+x+x；
此时当x＝时，y有最大值2+；
当≤x≤2时，过点E作EQ⊥AB交于Q，过点F作FP⊥AB交于P，
∴AB+BF＝x，DA+DE＝x，
∵AB＝4，AD＝2，
∴BE＝2﹣x+2，BF＝x﹣4，
∵PF∥DM，
∴＝，即＝，
∴PF＝x﹣2，
∵EQ∥DM，
∴＝，即＝，
∴EQ＝+1﹣x，
∴y＝×AB×（EQ﹣PF）＝×4×（+1﹣x﹣x+2）＝6+2﹣x﹣x；
此时当x＝时，y有最大值2+；
综上所述：当0≤x≤2时，y＝x2；当2≤x≤时，y＝﹣x2+x+x；当≤x≤2时，y＝6+2﹣x﹣x；y的最大值为2+；
（3）连接DH，
∵AH＝HB，AB＝4，
∴AH＝1，
∴DH⊥AB，
∵M是DF的中点，
∴HM＝DM＝MF，
∵EM＝HM，
∴EM＝DF，
∴△EDF是直角三角形，
∴EF⊥AD，
∵AD⊥BD，
∴EF∥BD．





五．切线的判定与性质（共1小题）
10．（2022•德阳）如图，AB是⊙O的直径，CD是⊙O的弦，AB⊥CD，垂足是点H，过点C作直线分别与AB，AD的延长线交于点E，F，且∠ECD＝2∠BAD．
（1）求证：CF是⊙O的切线；
（2）如果AB＝10，CD＝6，
①求AE的长；
②求△AEF的面积．

【解答】（1）证明：连接OC，如图，

∵AB是⊙O的直径，AB⊥CD，
∴，
∴∠CAB＝∠DAB．
∵∠COB＝2∠CAB，
∴∠COB＝2∠BAD．
∵∠ECD＝2∠BAD，
∴∠ECD＝∠COB．
∵AB⊥CD，
∴∠COB+∠OCH＝90°，
∴∠OCH+∠ECD＝90°，
∴∠OCE＝90°．
∴OC⊥CF．
∵OC是⊙O的半径，
∴CF是⊙O的切线；
（2）解：①∵AB＝10，
∴OA＝OB＝OC＝5，
∵AB是⊙O的直径，AB⊥CD，
∴CH＝DH＝CD＝3．
∴OH＝＝4，
∵OC⊥CF，CH⊥OE，
∴△OCH∽△OEC，
∴，
∴，
∴OE＝．
∴AE＝OA+OE＝5+＝；
②过点F作FG⊥AB，交AB的延长线于点G，如图，

∵∠OCF＝∠FGE＝90°，∠CEO＝∠GEF，
∴△OCE∽△FGE．
∴，
设FG＝4k，则FE＝5k，
∴EG＝＝3k，
∵DH⊥AB，FG⊥AB，
∴DH∥FG．
∴，
∴，
解得：k＝．
∴FG＝4k＝5．
∴△AEF的面积＝×AE•FG＝．
六．圆的综合题（共5小题）
11．（2022•绵阳）如图，AB为⊙O的直径，C为圆上的一点，D为劣弧的中点，过点D作⊙O的切线与AC的延长线交于点P，与AB的延长线交于点F，AD与BC交于点E．
（1）求证：BC∥PF；
（2）若⊙O的半径为，DE＝1，求AE的长度；
（3）在（2）的条件下，求△DCP的面积．

【解答】（1）证明：连接OD，如图，

∵D为劣弧的中点，
∴，
∴OD⊥BC．
∵PF是⊙O的切线，
∴OD⊥PF，
∴BC∥PF；
（2）连接OD，BD，如图，

设AE＝x，则AD＝1+x．
∵D为劣弧的中点，
∴，
∴CD＝BD，∠DCB＝∠CAD．
∵∠CDE＝∠ADC，
∴△CDE∽△ADC，
∴，
∴CD2＝DE•AD＝1×（1+x）＝1+x．
∴BD2＝1+x．
∵AB为⊙O的直径，
∴∠ADB＝90°，
∴AD2+BD2＝AB2．
∵⊙O的半径为，
∴AB＝2．
∴，
解得：x＝3或x＝﹣6（不合题意，舍去），
∴AE＝3．
（3）连接OD，BD，设OD与BC交于点H，如图，

由（2）知：AE＝3，AD＝AE+DE＝4，DB＝＝2，
∵∠ADB＝90°，
∴cos∠DAB＝＝．
∵OA＝OD，
∴∠DAB＝∠ADO，
∴cos∠ADO＝cos∠DAB＝．
∵OH⊥BC，
∴BH＝CH，cos∠ADO＝，
∴DH＝DE×＝．
∴OH＝OD﹣DH＝﹣＝．
∴BH＝＝，
∴CH＝BH＝．
∵AB为⊙O的直径，
∴∠ACB＝90°，
由（1）知：OD⊥PD，OH⊥BC，
∴四边形CHDP为矩形，
∴∠P＝90°，CP＝DH＝，DP＝CH＝，
∴△DCP的面积＝CP•DP＝．
12．（2022•达州）如图，在Rt△ABC中，∠C＝90°，点O为AB边上一点，以OA为半径的⊙O与BC相切于点D，分别交AB，AC边于点E，F．
（1）求证：AD平分∠BAC；
（2）若BD＝3，tan∠CAD＝，求⊙O的半径．

【解答】（1）证明：连接OD．
∵BC是⊙O的切线，OD是⊙O半径，D是切点，
∴OD⊥BC，
∴∠ODB＝∠C＝90°，
∴OD∥AC，
∴∠ODA＝∠CAD，
∵OD＝OA，
∴∠ODA＝∠OAD，
∴∠OAD＝∠CAD，
∴AD平分∠BAC；

（2）解：连接DE，过点D作DT⊥AB于点T，
∵AE是直径，
∴∠ADE＝90°，
∵tan∠CAD＝tan∠DAE＝，
∴＝，
设DE＝k，AD＝2k，则AE＝k，
∵•DE•AD＝•AE•DT，
∴DT＝k，
∴OT＝＝＝k，
∵tan∠DOT＝＝，
∴＝，
∴k＝，
∴OD＝k＝，
∴⊙O的半径为．

13．（2022•凉山州）如图，已知半径为5的⊙M经过x轴上一点C，与y轴交于A、B两点，连接AM、AC，AC平分∠OAM，AO+CO＝6．
（1）判断⊙M与x轴的位置关系，并说明理由；
（2）求AB的长；
（3）连接BM并延长交⊙M于点D，连接CD，求直线CD的解析式．

【解答】解：（1）猜测⊙M与x轴相切，理由如下：
如图，连接OM，
∵AC平分∠OAM，
∴∠OAC＝∠CAM，
又∵MC＝AM，
∴∠CAM＝∠ACM，
∴∠OAC＝∠ACM，
∴OA∥MC，
∵OA⊥x轴，
∴MC⊥x轴，
∵CM是半径，
∴⊙M与x轴相切．
（2）如图，过点M作MN⊥y轴于点N，
∴AN＝BN＝AB，
∵∠MCO＝∠AOC＝∠MNA＝90°，
∴四边形MNOC是矩形，
∴NM＝OC，MC＝ON＝5，
设AO＝m，则OC＝6﹣m，
∴AN＝5﹣m，
在Rt△ANM中，由勾股定理可知，AM2＝AN2+MN2，
∴52＝（5﹣m）2+（6﹣m）2，
解得m＝2或m＝9（舍去），
∴AN＝3，
∴AB＝6．
（3）如图，连接AD与CM交于点E，
∵BD是直径，
∴∠BAD＝90°，
∴AD∥x轴，
∴AD⊥MC，
由勾股定理可得AD＝8，
∴D（8，﹣2）．
由（2）可得C（4，0），
设直线CD的解析式为：y＝kx+b，
∴，解得．
∴直线CD的解析式为：y＝﹣x+2．

14．（2022•成都）如图，在Rt△ABC中，∠ACB＝90°，以BC为直径作⊙O，交AB边于点D，在上取一点E，使＝，连接DE，作射线CE交AB边于点F．
（1）求证：∠A＝∠ACF；
（2）若AC＝8，cos∠ACF＝，求BF及DE的长．

【解答】（1）证明：∵＝，
∴∠BCF＝∠FBC，
∵∠ACB＝90°，
∴∠A+∠FBC＝90°，∠ACF+∠BCF＝90°，
∴∠A＝∠ACF；

（2）解：连接CD．
∵∠A＝∠ACF，∠FBC＝∠BCF，
∴AF＝FC＝FB，
∴cos∠A＝cos∠ACF＝＝，
∵AC＝8，
∴AB＝10，BC＝6，
∵BC是直径，
∴∠CDB＝90°，
∴CD⊥AB，
∵S△ABC＝•AC•BC＝•AB•CD，
∴CD＝＝，
∴BD＝＝＝，
∵BF＝AF＝5，
∴DF＝BF﹣BD＝5﹣＝，
∵∠DEF+∠DEC＝180°，∠DEC+∠B＝180°，
∴∠DEF＝∠B＝∠BCF，
∴DE∥CB，
∴△DEF∽△BCF，
∴＝，
∴＝，
∴DE＝．

15．（2022•泸州）如图，点C在以AB为直径的⊙O上，CD平分∠ACB交⊙O于点D，交AB于点E，过点D作⊙O的切线交CO的延长线于点F．
（1）求证：FD∥AB；
（2）若AC＝2，BC＝，求FD的长．

【解答】（1）证明：连接OD．
∵DF是⊙O的切线，
∴OD⊥DF，
∵CD平分∠ACB，
∴＝，
∴OD⊥AB，
∴AB∥DF；

（2）解：过点C作CH⊥AB于点H．
∵AB是直径，
∴∠ACB＝90°，
∵BC＝，AC＝2，
∴AB＝＝＝5，
∵S△ABC＝•AC•BC＝•AB•CH，
∴CH＝＝2，
∴BH＝＝1，
∴OH＝OB﹣BH＝﹣1＝，
∵DF∥AB，
∴∠COH＝∠F，
∵∠CHO＝∠ODF＝90°，
∴△CHO∽△ODF，
∴＝，
∴＝，
∴DF＝．

七．几何变换综合题（共1小题）
16．（2022•广元）在Rt△ABC中，AC＝BC，将线段CA绕点C旋转α（0°＜α＜90°），得到线段CD，连接AD、BD．
（1）如图1，将线段CA绕点C逆时针旋转α，则∠ADB的度数为 　135°　；
（2）将线段CA绕点C顺时针旋转α时
①在图2中依题意补全图形，并求∠ADB的度数；
②若∠BCD的平分线CE交BD于点F，交DA的延长线于点E，连结BE．用等式表示线段AD、CE、BE之间的数量关系，并证明．


【解答】解：（1）在Rt△ABC中，AC＝BC，将线段CA绕点C旋转α（0°＜α＜90°），
∴CD＝CA＝CB，∠ACD＝α，
∴∠BCD＝90°﹣α，
∵CD＝CA，CD＝CB，
∴∠ADC＝＝90°﹣，∠BDC＝＝45°+，
∴∠ADB＝∠ADC+∠BDC＝90°﹣+45°+＝135°，
故答案为：135°；

（2）①依题意补全图形如图，

由旋转得：CD＝CA＝CB，∠ACD＝α，
∴∠BCD＝90°+α，
∵CD＝CA，CD＝CB，
∴∠ADC＝＝90°﹣，∠BDC＝＝45°﹣，
∴∠ADB＝∠ADC﹣∠BDC＝90°﹣﹣45°+＝45°；
②CE＝2BE﹣AD．
证明：过点C作CG∥BD，交EB的延长线于点G，

∵BC＝CD，CE平分∠BCD，
∴CE垂直平分BD，
∴BE＝DE，∠EFB＝90°，
由①知，∠ADB＝45°，
∴∠EBD＝∠EDB＝45°，
∴∠FEB＝45°，
∵BD∥CG，
∴∠ECG＝∠EFB＝90°，∠G＝∠EBD＝45°，
∴EC＝CG，EG＝EC，
∵∠ACE＝90°﹣∠ECB，∠BCG＝90°﹣∠ECB，
∴∠ACE＝∠BCG，
∵AC＝BC，
∴△ACE≌△BCG（SAS），
∴AE＝BG，
∵EG＝EB+BG＝EB+AE＝EB+ED﹣AD＝2EB﹣AD，
∴CE＝2BE﹣AD．