高中数学湘教版（2019）必修 第一册2.1 相等关系与不等关系综合训练题

2.1  相等关系与不等关系 同步课时训练

学校：___________姓名：___________班级：___________考号：___________

一、选择题(共40分)

1、(4分)不等式对任意a，恒成立，则实数x的取值范围是(   )

A. B. C. D.

2、(4分)若，则当取得最大值时，x的值为(   )

A. B. C. D.

3、(4分)若，且，则下列四个数中最大的是(   )

A. B.b C.ab D.

4、(4分)已知，函数在处的切线与直线平行，则的最小值是（    ）

A.2 B.3 C.4 D.5

5、(4分)已知，，，则M与N的大小关系为(   )

A. B. C. D.

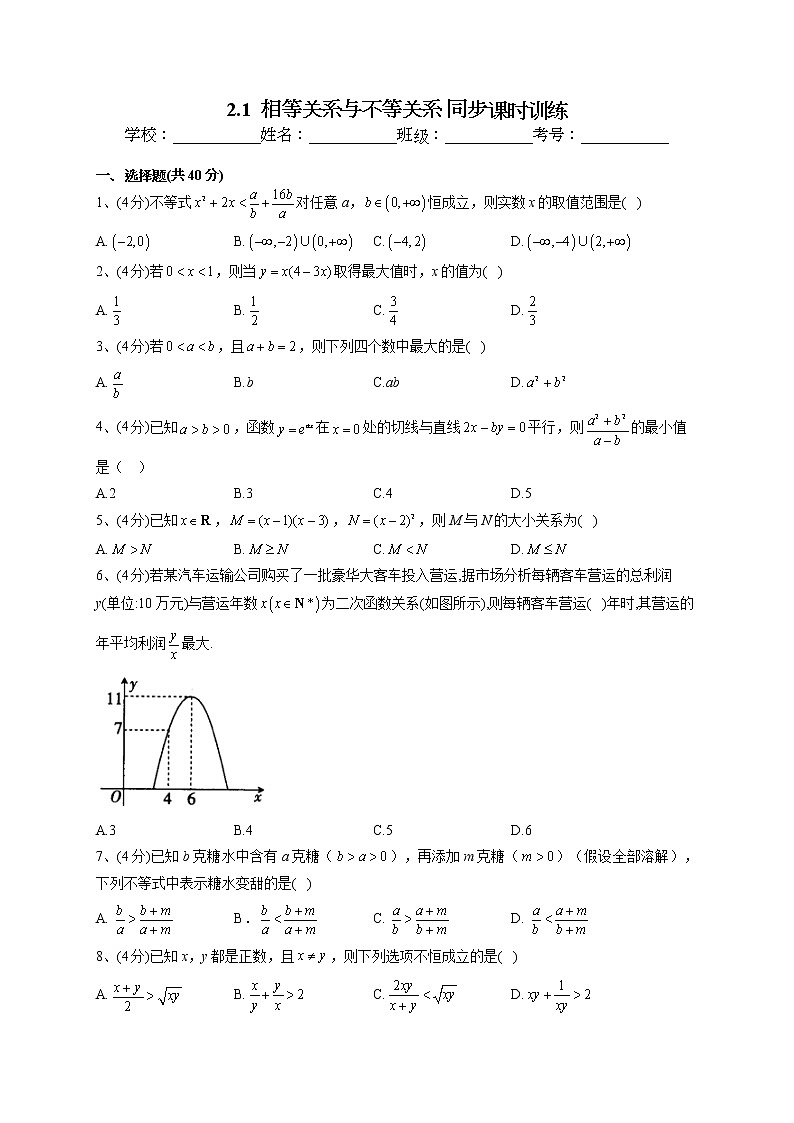
6、(4分)若某汽车运输公司购买了一批豪华大客车投入营运,据市场分析每辆客车营运的总利润y(单位:10万元)与营运年数为二次函数关系(如图所示),则每辆客车营运(   )年时,其营运的年平均利润最大.

A.3 B.4 C.5 D.6

7、(4分)已知b克糖水中含有a克糖（），再添加m克糖（）（假设全部溶解），下列不等式中表示糖水变甜的是(   )

A.         B．       C.         D.

8、(4分)已知x，y都是正数，且，则下列选项不恒成立的是(   )

A. B. C. D.

9、(4分)已知，且，则mn有(   )

A.最大值1 B.最大值2 C.最小值1 D.最小值2

10、(4分)已知a，b为正实数，直线与曲线相切，则的最小值是(   )

A.6 B. C.8 D.

二、填空题(共25分)

11、(5分)已知a，b均为正数，且，则ab的最大值为________，的最小值为__________.

12、(5分)给出下列命题：

①若，，则；②若，则；③若，则；④若，则.

其中正确命题的序号是___________.（填上所有正确的序号）

13、(5分)下列四个条件：①，②，③，④.其中能使得成立的是___________.（填上所有正确的序号）

14、(5分)已知在中,,则的取值范围是______,若,则的最小值是___________.

15、(5分)已知，，且满足，则的最小值为_____________.

三、解答题(共35分)

16、(8分)已知，满足.

（1）求证：；

（2）现推广：把的分子改为另一个大于1的正整数p，使对任意恒成立，试写出一个p，并证明之.

17、(9分)某工厂某种产品的月固定成本为10万元，每生产x件，需另投入成本为C，当月产量不足30件时，（万元）.当月产量不小于30件时，（万元）.每件商品售价为5万元，通过市场分析，该厂生产的商品能全部售完.因设备问题，该厂月生产量不超过50件.

（1）写出月利润L（万元）关于月产量x（件）的表达式；

（2）当月产量为多少件时，该厂在这一商品的生产中所获月利润最大？

18、(9分)已知正数a，b满足.

（1）若，，求的值；

（2）求的最大值.

19、(9分)某地为了加快推进垃圾分类工作，新建了一个垃圾处理厂，每月最少要处理300吨垃圾，最多要处理600吨垃圾，月处理成本（元）与月处理量x（吨）之间的函数关系可近似地表示为.

（1）写出自变量x的取值范围；

（2）为使每吨平均处理成本最低（如处理500吨垃圾时每吨垃圾平均处理成本为），该厂每月垃圾处理量应为多少吨？

参考答案

1、答案：C

解析：，当且仅当，即时取等号，不等式对任意a，恒成立，，，实数x的取值范围是.故选：C.

2、答案：D

解析：本题考查基本不等式的应用.，，当且仅当，即时，取得“=”.

3、答案：D

解析：本题考查基本不等式.因为，，所以，可得，（当且仅当时取等号）；因为，所以等号不成立，则，可得，（当且仅当时取等号）；因为，所以等号不成立，则，而，所以.综上可得，四个数中最大的是.

4、答案：C

解析：因为，则，因为切点为，则切线的斜率为，又因为切线与直线平行，所以，即，所以，当且仅当，即时，等号成立，则的最小值是4，故选：C.

5、答案：C

解析：本题考查作差法比较大小.由题意，，，则，所以，即，故选C项.

6、答案：C

解析：根据题意得到,抛物线的顶点为(6,11),过点(4,7),图象开口向下,设二次函数的解析式为,所以,解得,即,因为,所以,当且仅当,即时取等号.故选C.

7、答案：D

解析：因为b克糖水中含a克糖,所以糖水的“甜度”为,再加入克糖,糖水的“甜度”为,因为糖水更甜了,所以.

8、答案：D

解析：由基本不等式，，，，这三个不等式都是当且仅当时等号成立，而题中，因此等号都取不到，所以ABC三个不等式恒成立；

中当且仅当时取等号，如，即可取等号，D中不等式不恒成立.

9、答案：A

解析：，且，，当且仅当时取等号，有最大值1.故选A.

10、答案：C

解析：设切点为，

的导数为，

由题意可得，

又，，

解得，，

即有，因为a、b为正实数，

所以，

当且仅当时取等号，

故的最小值为8.

故选：C.

11、答案：2，

解析：由题意，得，当且仅当，即，时等号成立，所以，所以ab的最大值为2，，当，时取等号.

12、答案：②

解析：本题考查利用不等式的性质判断大小.①当时，不成立，故①不正确；
②由知，所以，即，
所以，故②正确；

③当，，命题不成立，故③不正确；
④当时，，故④不正确.

13、答案：④

解析：本题考查不等式的性质判断大小.，④能使它成立.

14、答案：；

解析：由题意得.若，则，当且仅当时取等号,所以的最小值是.

15、答案：7

解析：，由，

可得，当且仅当，即时等号成立，

则最小值为7.

16、答案： (1)见解析(2) 见解析

解析：(1) 证明 : 由 ，得 ，,
要证 ，
只要证 ，
左边

当且仅当 ，即 时等号成立；

(2)要使,
只至至,

左边

则 ， 可取 或 3
取 ，问题转化为.
证明如下 : 要证 ，
只需证明 ，
左边

当且仅当 ，即 时等号成立.

17、答案：（1）见解析

（2）当月产量为30件时，月获利润最大.

解析：（1）因为每件商品售价为5万元，所以x件商品销售额为5x万元，
依题意得，
当时，；
当时，.
（2）当时，，
对称轴为.
即当时，（万元）；
当时，，
当且仅当时，（万元）.

综上所述，当月产量为30件时，月获利润最大.

18、答案：（1）3

（2）见解析

解析：（1）由，可得，则.

（2）由（1）得，，
则

，
当且仅当中，即时，等号成立.

19、答案：(1).

(2)400吨.

解析：(1)；

(2)依题意，每吨平均处理成本元，

因为，

当且仅当即时，等号成立，

所以，

所以该厂每月垃圾处理量为400吨时，

每吨平均处理成本最低为100元.