数学必修 第一册第五章 三角函数5.4 三角函数的图象与性质教学课件ppt

这是一份数学必修 第一册第五章 三角函数5.4 三角函数的图象与性质教学课件ppt，共28页。PPT课件主要包含了三角函数，基础梳理，思考应用，五点法，自测自评，用“五点法”作图，跟踪训练，答案B，用图象变换法作简图等内容，欢迎下载使用。
三角函数的图象与性质 正弦函数、余弦函数的图象
1．理解：利用单位圆中的正弦线画出正弦函数图象．2．掌握“五点法”作图的方法，能熟练用“五点法”作出正弦函数、余弦函数的图象．
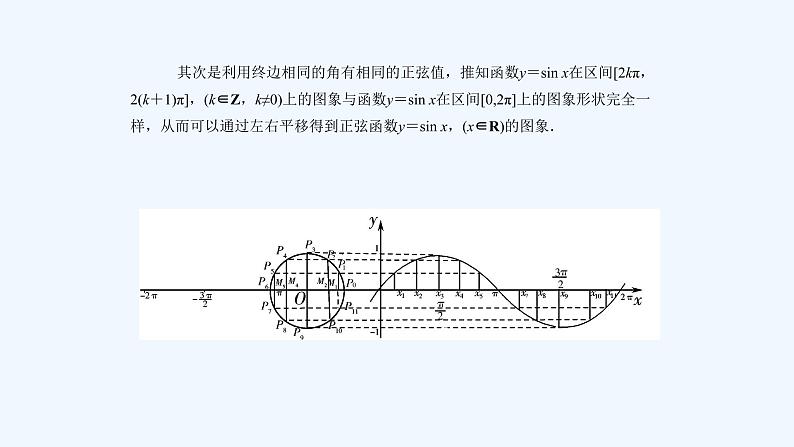
一、正弦函数、余弦函数的图象1．正弦函数、余弦函数的概念：若对于任意给定的一个实数x，都有唯一确定的值sin x(或cs x)与之对应，则称由这个对应法则所确定的函数________(或________)为正弦函数(或余弦函数)，其定义域是________．2．正弦函数和余弦函数的图象分别叫做________和________：(1)利用单位圆中的正弦线画函数y＝sin x的图象，其过程可以概括为以下两点：首先是等分单位圆、等分区间[0,2π]和正弦线的平移，进而得到函数y＝sin x在区间[0,2π]上的图象．
一、1.y＝sin x(或y＝cs x)　R　2.正弦曲线　余弦曲线
其次是利用终边相同的角有相同的正弦值，推知函数y＝sin x在区间[2kπ，2(k＋1)π]，(k∈Z，k≠0)上的图象与函数y＝sin x在区间[0,2π]上的图象形状完全一样，从而可以通过左右平移得到正弦函数y＝sin x，(x∈R)的图象．
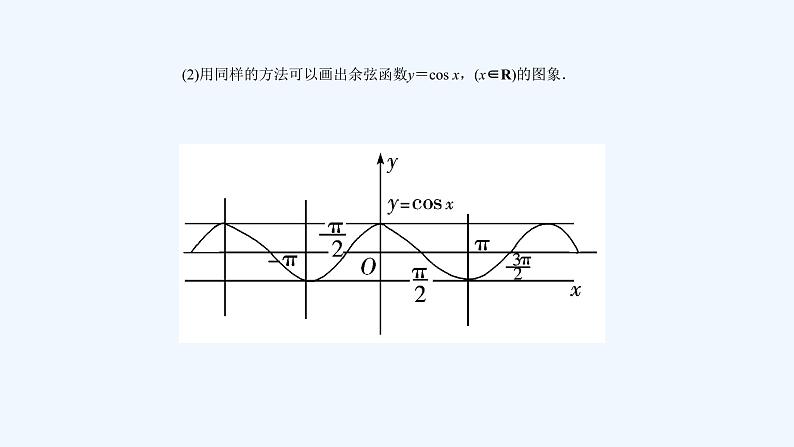
(2)用同样的方法可以画出余弦函数y＝cs x，(x∈R)的图象．
1．你能根据诱导公式，以正弦函数图象为基础，通过适当的图形变换得到余弦函数的图象？
解析：根据诱导公式cs x＝sin ，可以把正弦函数y＝sin x，(x∈R)的图象向左平移 单位即得余弦函数y＝cs x，(x∈R)的图象．作简图如下：
二、五点法作图1．画正弦函数和余弦函数在[0,2π]上的简图：在所作图形的精确度要求不太高时，我们常用“______”作简图：(1)对正弦函数y＝sin x，取五点：A(0,0)，B ，C(π，0)，D ，E(2π，0)．这五点描出后，正弦函数y＝ sin x，x∈[0,2π]的图象就基本确定了．(2)对余弦函数y＝cs x，取五点：A(0,1)，B ，C(π，－1)，D ，E(2π，1)．这五点描出后，余弦函数y＝cs x，x∈[0,2π]的图象也就基本确定了．
2．五点作图的基本步骤有哪些？
解析：五点作图法必须有三步：列表、描点、连线．连线时要注意曲线的光滑和凸凹．
1．下列各式中，值为－1的是(　　)A．sin　　　B．cs　　　C．sin π　　　D．cs π
解析：因为sin ＝1；cs ＝0；sin π＝0；cs π＝－1.故选D.答案： D
用“五点法”作函数y＝2－sin x，x∈[0,2π]的简图．分析：用“五点法”作函数y＝sin x，x∈[0,2π]简图时的五个点为：A(0,0)，B ，C (π,0) ，D ，E (2π,0)解析：列表：描点，并用光滑曲线连接起来．图略．点评：用“五点法”作图一般是先取函数y＝sin x图象上对应的五个点作为参照．
1．用“五点法”作函数y＝cs 在一个周期内的简图．
解析： 列表：描点，并用光滑曲线连接起来．图略．
有关三角函数的定义域
写出不等式sin x≥ 的解集．分析：解答本题可利用数形结合，分别画出y＝sin x和y＝ 的图象，通过图象写出不等式的解集．解析：画出y＝sin x，x∈[0,2π]的图象，及y＝ ，
点评：本题易出现解集为 的错误，错误的原因是忽视了定义域为R.
2．已知x∈(0,2π)，在同一坐标系中，画出y＝sin x和y＝cs x的图象，并由图象求出使sin x