湖南省各地区2022年中考数学真题按题型难易度分层分类汇编-09解答题（基础题）2

这是一份湖南省各地区2022年中考数学真题按题型难易度分层分类汇编-09解答题（基础题）2，共34页。试卷主要包含了﹣1+|1﹣|﹣2sin60°，﹣1﹣，2022+﹣2sin30°，先化简，再求值，解不等式组等内容，欢迎下载使用。

湖南省各地区2022年中考数学真题按题型难易度分层分类汇编-09解答题（基础题）2
一．实数的运算（共3小题）
1．（2022•娄底）计算：（2022﹣π）0+（）﹣1+|1﹣|﹣2sin60°．
2．（2022•怀化）计算：（3.14﹣π）0+|﹣1|+（）﹣1﹣．
3．（2022•株洲）计算：（﹣1）2022+﹣2sin30°．
二．整式的混合运算—化简求值（共1小题）
4．（2022•衡阳）先化简，再求值．
（a+b）（a﹣b）+b（2a+b），其中a＝1，b＝﹣2．
三．分式的化简求值（共3小题）
5．（2022•娄底）先化简，再求值：（x+2+）÷，其中x是满足条件x≤2的合适的非负整数．
6．（2022•湘潭）先化简，再求值：÷﹣•，其中x＝2．
7．（2022•邵阳）先化简，再从﹣1，0，1，中选择一个合适的x值代入求值．
（+）÷．
四．分式方程的应用（共1小题）
8．（2022•常德）小强的爸爸平常开车从家中到小强奶奶家，匀速行驶需要4小时．某天，他们以平常的速度行驶了的路程时遇到了暴雨，立即将车速减少了20千米/小时，到达奶奶家时共用了5小时，问小强家到他奶奶家的距离是多少千米？
五．一元一次不等式的应用（共1小题）
9．（2022•邵阳）2022年2月4日至20日冬季奥运会在北京举行．某商店特购进冬奥会纪念品“冰墩墩”摆件和挂件共180个进行销售．已知“冰墩墩”摆件的进价为80元/个，“冰墩墩”挂件的进价为50元/个．
（1）若购进“冰墩墩”摆件和挂件共花费了11400元，请分别求出购进“冰墩墩”摆件和挂件的数量．
（2）该商店计划将“冰墩墩”摆件售价定为100元/个，“冰墩墩”挂件售价定为60元/个，若购进的180个“冰墩墩”摆件和挂件全部售完，且至少盈利2900元，求购进的“冰墩墩”挂件不能超过多少个？
六．解一元一次不等式组（共2小题）
10．（2022•常德）解不等式组．
11．（2022•怀化）解不等式组，并把解集在数轴上表示出来．


七．反比例函数系数k的几何意义（共1小题）
12．（2022•株洲）如图所示，在平面直角坐标系xOy中，点A、B分别在函数y1＝（x＜0）、y2＝（x＞0，k＞0）的图象上，点C在第二象限内，AC⊥x轴于点P，BC⊥y轴于点Q，连接AB、PQ，已知点A的纵坐标为﹣2．
（1）求点A的横坐标；
（2）记四边形APQB的面积为S，若点B的横坐标为2，试用含k的代数式表示S．

八．反比例函数与一次函数的交点问题（共1小题）
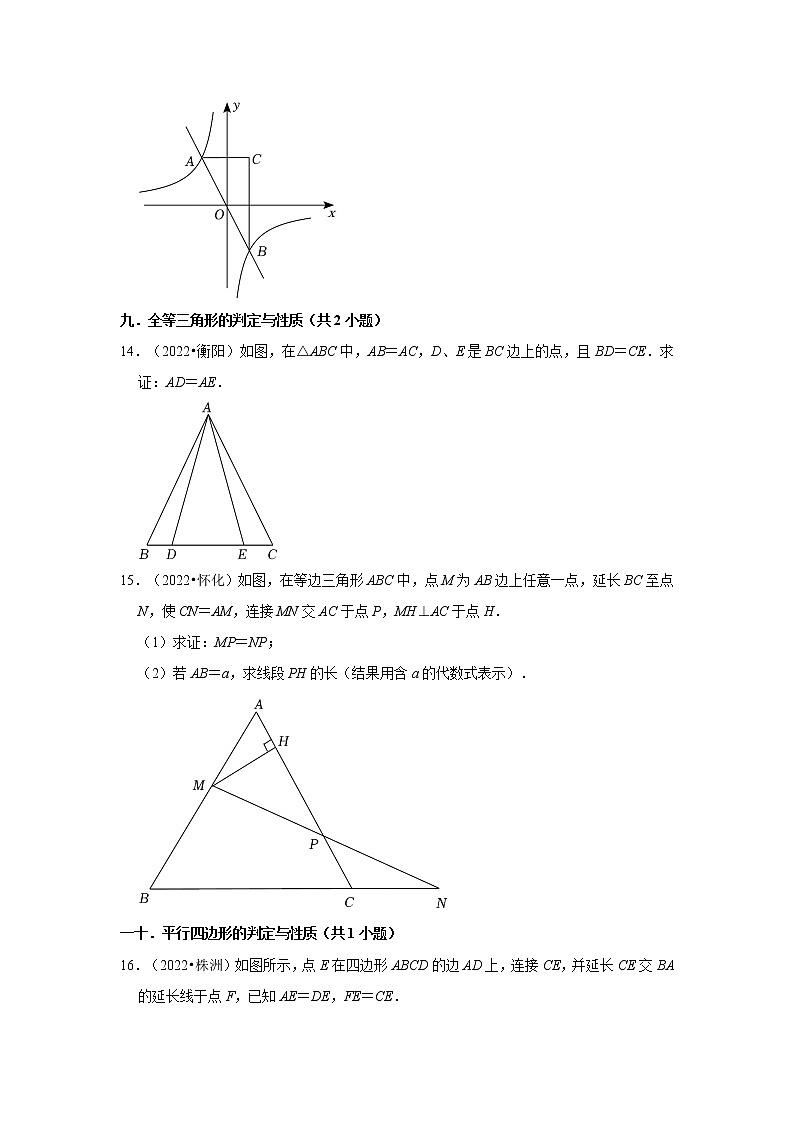
13．（2022•岳阳）如图，反比例函数y＝（k≠0）与正比例函数y＝mx（m≠0）的图象交于点A（﹣1，2）和点B，点C是点A关于y轴的对称点，连接AC，BC．
（1）求该反比例函数的解析式；
（2）求△ABC的面积；
（3）请结合函数图象，直接写出不等式＜mx的解集．

九．全等三角形的判定与性质（共2小题）
14．（2022•衡阳）如图，在△ABC中，AB＝AC，D、E是BC边上的点，且BD＝CE．求证：AD＝AE．

15．（2022•怀化）如图，在等边三角形ABC中，点M为AB边上任意一点，延长BC至点N，使CN＝AM，连接MN交AC于点P，MH⊥AC于点H．
（1）求证：MP＝NP；
（2）若AB＝a，求线段PH的长（结果用含a的代数式表示）．

一十．平行四边形的判定与性质（共1小题）
16．（2022•株洲）如图所示，点E在四边形ABCD的边AD上，连接CE，并延长CE交BA的延长线于点F，已知AE＝DE，FE＝CE．
（1）求证：△AEF≌△DEC；
（2）若AD∥BC，求证：四边形ABCD为平行四边形．

一十一．正方形的判定（共1小题）
17．（2022•邵阳）如图，在菱形ABCD中，对角线AC，BD相交于点O，点E，F在对角线BD上，且BE＝DF，OE＝OA．
求证：四边形AECF是正方形．

一十二．圆周角定理（共1小题）
18．（2022•怀化）如图，点A，B，C，D在⊙O上，＝．
求证：（1）AC＝BD；
（2）△ABE∽△DCE．

一十三．切线的性质（共1小题）
19．（2022•邵阳）如图，已知DC是⊙O的直径，点B为CD延长线上一点，AB是⊙O的切线，点A为切点，且AB＝AC．
（1）求∠ACB的度数；
（2）若⊙O的半径为3，求圆弧的长．

一十四．弧长的计算（共1小题）
20．（2022•湘潭）如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣1，1），B（﹣4，0），C（﹣2，2）．将△ABC绕原点O顺时针旋转90°后得到△A1B1C1．
（1）请写出A1、B1、C1三点的坐标：
A1　 　，B1　 　，C1　 　；
（2）求点B旋转到点B1的弧长．

一十五．圆的综合题（共1小题）
21．（2022•永州）如图，已知AB，CE是⊙O的直径，BM是⊙O的切线，点D在EA的延长线上，AC，OD交于点F，∠MBC＝∠ACD．
（1）求证：∠MBC＝∠BAC；
（2）求证：AE＝AD；
（3）若△OFC的面积S1＝4，求四边形AOCD的面积S．

一十六．轴对称-最短路线问题（共1小题）
22．（2022•永州）为提高耕地灌溉效率，小明的爸妈准备在耕地A、B、C、D四个位置安装四个自动喷洒装置（如图1所示），A、B、C、D四点恰好在边长为50米的正方形的四个顶点上，为了用水管将四个自动喷洒装置相互连通，爸妈设计了如下两个水管铺设方案（各图中实线为铺设的水管）．
方案一：如图2所示，沿正方形ABCD的三边铺设水管；
方案二：如图3所示，沿正方形ABCD的两条对角线铺设水管．
（1）请通过计算说明上述两方案中哪个方案铺设水管的总长度更短；
（2）小明看了爸妈的方案后，根据“蜂集原理”重新设计了一个方案（如图4所示）．

满足∠AEB＝∠CFD＝120°，AE＝BE＝CF＝DF，EF∥AD．请将小明的方案与爸妈的方案比较，判断谁的方案中铺设水管的总长度更短，并说明理由．（参考数据：≈1.4，≈1.7）

一十七．相似三角形的判定与性质（共1小题）
23．（2022•常德）如图，已知AB是⊙O的直径，BC⊥AB于B，E是OA上的一点，ED∥BC交⊙O于D，OC∥AD，连接AC交ED于F．
（1）求证：CD是⊙O的切线；
（2）若AB＝8，AE＝1，求ED，EF的长．

一十八．特殊角的三角函数值（共1小题）
24．（2022•岳阳）计算：|﹣3|﹣2tan45°+（﹣1）2022﹣（﹣π）0．
一十九．解直角三角形的应用-坡度坡角问题（共1小题）
25．（2022•株洲）如图（Ⅰ）所示，某登山运动爱好者由山坡①的山顶点A处沿线段AC至山谷点C处，再从点C处沿线段CB至山坡②的山顶点B处．如图（Ⅱ）所示，将直线l视为水平面，山坡①的坡角∠ACM＝30°，其高度AM为0.6千米，山坡②的坡度i＝1：1，BN⊥l于N，且CN＝千米．
（1）求∠ACB的度数；
（2）求在此过程中该登山运动爱好者走过的路程．
二十．解直角三角形的应用-方向角问题（共1小题）
26．（2022•邵阳）如图，一艘轮船从点A处以30km/h的速度向正东方向航行，在A处测得灯塔C在北偏东60°方向上，继续航行1h到达B处，这时测得灯塔C在北偏东45°方向上，已知在灯塔C的四周40km内有暗礁，问这艘轮船继续向正东方向航行是否安全？并说明理由．（提示：≈1.414，≈1.732）

二十一．扇形统计图（共2小题）
27．（2022•湘潭）百年青春百年梦，初心献党向未来．为热烈庆祝中国共产主义青年团成立10周年，继承先烈遗志，传承“五四”精神．某中学在“做新时代好少年，强国有我”的系列活动中，开展了“好书伴我成长”的读书活动．为了解5月份八年级学生的读书情况，随机调查了八年级20名学生读书数量（单位：本），并进行了以下数据的整理与分析：
数据收集
2 5 3 5 4 6 1 5 3 4
3 6 7 5 8 3 4 7 3 4
数据整理
本数
0＜x≤2
2＜x≤4
4＜x≤6
6＜x≤8
组别
A
B
C
D
频数
2
m
6
3
数据分析 绘制成不完整的扇形统计图：
依据统计信息回答问题：
（1）在统计表中，m＝　 　；
（2）在扇形统计图中，C部分对应的圆心角的度数为 　 　；
（3）若该校八年级学生人数为200人，请根据上述调查结果，估计该校八年级学生读书在4本以上的人数．

28．（2022•怀化）电视剧《一代洪商》在中央电视台第八套播出后，怀化市各旅游景点知名度得到显著提高．为全面提高旅游服务质量，旅游管理部门随机抽取了100名游客进行满意度调查，并绘制成如下不完整的频数分布表和扇形统计图．
频数分布表
满意程度
频数（人）
频率
非常满意
50
0.5
满意
30
0.3
一般
a
c
不满意
b
0.05
合计
100
1
根据统计图表提供的信息，解答下列问题：
（1）a＝　 　，b＝　 　，c＝　 　；
（2）求扇形统计图中表示“一般”的扇形圆心角α的度数；
（3）根据调查情况，请你对各景点的服务提一至两条合理建议．

二十二．条形统计图（共2小题）
29．（2022•常德）2020年7月，教育部印发的《大中小学劳动教育指导纲要（试行）》中明确要求中小学劳动教育课平均每周不少于1课时，初中生平均每周劳动时间不少于3小时．某初级中学为了解学生劳动教育的情况，从本校学生中随机抽取了500名进行问卷调查．如图是根据此次调查结果得到的统计图．
请根据统计图回答下列问题：
（1）本次调查中，平均每周劳动时间符合教育部要求的人数占被调查人数的百分比为多少？
（2）若该校有2000名学生，请估计最喜欢的劳动课程为木工的有多少人．
（3）请你根据本次问卷调查的结果给同学和学校各提一条合理化建议．

30．（2022•娄底）按国务院教育督导委员会办公室印发的《关于组织责任督学进行“五项管理”督导的通知》要求，各中小学校积极行动，取得了良好的成绩．某中学随机抽取了部分学生对他们一周的课外阅读时间（A：10h以上，B：8h～10h，C：6h～8h，D：6h以下）进行问卷调查，将所得数据进行分类，统计绘制了如下不完整的统计图．请根据图中的信息，解答下列问题：

（1）本次调查的学生共 　 　名；
（2）a＝　 　，b＝　 　；
（3）补全条形统计图．

二十三．列表法与树状图法（共2小题）
31．（2022•岳阳）守护好一江碧水，打造长江最美岸线．江豚，麋鹿，天鹅已成为岳阳“吉祥三宝”的新名片．某校生物兴趣小组设计了3张环保宣传卡片，正面图案如图所示，它们除此之外完全相同．
（1）将这3张卡片背面朝上，洗匀，从中随机抽取一张，则抽取的卡片正面图案恰好是“麋鹿”的概率为 　 　；
（2）将这3张卡片背面朝上，洗匀，从中随机抽取一张，不放回，再从剩余的两张卡片中随机抽取一张，请用列表或画树状图的方法，求抽取的卡片正面图案恰好是“江豚”和“天鹅”的概率．

32．（2022•湘潭）5月30日是全国科技工作者日，某校准备举办“走近科技英雄，讲好中国故事”的主题比赛活动．八年级（一）班由A1、A2、A3三名同学在班上进行初赛，推荐排名前两位的同学参加学校决赛．
（1）请写出在班上初赛时，这三名同学讲故事顺序的所有可能结果；
（2）若A1、A2两名同学参加学校决赛，学校制作了编号为A、B、C的3张卡片（如图，除编号和内容外，其余完全相同），放在一个不透明的盒子里．先由A1随机摸取1张卡片记下编号，然后放回，再由A2随机摸取1张卡片记下编号，根据模取的卡片内容讲述相关英雄的故事．求A1、A2两人恰好讲述同一名科技英雄故事的概率（请用“画树状图”或“列表”等方法写出分析过程）．



湖南省各地区2022年中考数学真题按题型难易度分层分类汇编-09解答题（基础题）2
参考答案与试题解析
一．实数的运算（共3小题）
1．（2022•娄底）计算：（2022﹣π）0+（）﹣1+|1﹣|﹣2sin60°．
【解答】解：原式＝1+2+﹣1﹣2×
＝1+2+﹣1﹣
＝2．
2．（2022•怀化）计算：（3.14﹣π）0+|﹣1|+（）﹣1﹣．
【解答】解：原式＝1+﹣1+2﹣2
＝2﹣．
3．（2022•株洲）计算：（﹣1）2022+﹣2sin30°．
【解答】解：原式＝1+3﹣2×
＝1+3﹣1
＝3．
二．整式的混合运算—化简求值（共1小题）
4．（2022•衡阳）先化简，再求值．
（a+b）（a﹣b）+b（2a+b），其中a＝1，b＝﹣2．
【解答】解：（a+b）（a﹣b）+b（2a+b）
＝a2﹣b2+2ab+b2
＝a2+2ab，
将a＝1，b＝﹣2代入上式得：
原式＝12+2×1×（﹣2）
＝1﹣4
＝﹣3．
三．分式的化简求值（共3小题）
5．（2022•娄底）先化简，再求值：（x+2+）÷，其中x是满足条件x≤2的合适的非负整数．
【解答】解：原式＝（+）÷
＝•
＝，
∵x≠0且x﹣2≠0，
∴x≠0且x≠2，
∴x＝1，
则原式＝＝﹣1．
6．（2022•湘潭）先化简，再求值：÷﹣•，其中x＝2．
【解答】解：原式＝•（x+3）（x﹣3）﹣•
＝x+3﹣1
＝x+2，
当x＝2时，
原式＝2+2＝4．
7．（2022•邵阳）先化简，再从﹣1，0，1，中选择一个合适的x值代入求值．
（+）÷．
【解答】解：原式＝•
＝，
又∵x≠﹣1，0，1，
∴x可以取，此时原式＝＝．
四．分式方程的应用（共1小题）
8．（2022•常德）小强的爸爸平常开车从家中到小强奶奶家，匀速行驶需要4小时．某天，他们以平常的速度行驶了的路程时遇到了暴雨，立即将车速减少了20千米/小时，到达奶奶家时共用了5小时，问小强家到他奶奶家的距离是多少千米？
【解答】解：设平常的速度是x千米/小时，
根据题意，得，
解得x＝60，
经检验，x＝60是原方程的根，
4×60＝240（千米），
答：小强家到他奶奶家的距离是240千米．
五．一元一次不等式的应用（共1小题）
9．（2022•邵阳）2022年2月4日至20日冬季奥运会在北京举行．某商店特购进冬奥会纪念品“冰墩墩”摆件和挂件共180个进行销售．已知“冰墩墩”摆件的进价为80元/个，“冰墩墩”挂件的进价为50元/个．
（1）若购进“冰墩墩”摆件和挂件共花费了11400元，请分别求出购进“冰墩墩”摆件和挂件的数量．
（2）该商店计划将“冰墩墩”摆件售价定为100元/个，“冰墩墩”挂件售价定为60元/个，若购进的180个“冰墩墩”摆件和挂件全部售完，且至少盈利2900元，求购进的“冰墩墩”挂件不能超过多少个？
【解答】解：（1）设购进“冰墩墩”摆件x个，“冰墩墩”挂件y个，
依题意得：，
解得：．
答：购进“冰墩墩”摆件80个，“冰墩墩”挂件100个．
（2）设购进“冰墩墩”挂件m个，则购进“冰墩墩”摆件（180﹣m）个，
依题意得：（60﹣50）m+（100﹣80）（180﹣m）≥2900，
解得：m≤70．
答：购进的“冰墩墩”挂件不能超过70个．
六．解一元一次不等式组（共2小题）
10．（2022•常德）解不等式组．
【解答】解：由5x﹣1＞3x﹣4，得：x＞﹣，
由﹣≤﹣x，得：x≤1，
则不等式组的解集为﹣＜x≤1．
11．（2022•怀化）解不等式组，并把解集在数轴上表示出来．


【解答】解：，
解不等式①，得：x＞2，
解不等式②，得：x≤3，
∴原不等式组的解集是2＜x≤3，
其解集在数轴上表示如下：
．
七．反比例函数系数k的几何意义（共1小题）
12．（2022•株洲）如图所示，在平面直角坐标系xOy中，点A、B分别在函数y1＝（x＜0）、y2＝（x＞0，k＞0）的图象上，点C在第二象限内，AC⊥x轴于点P，BC⊥y轴于点Q，连接AB、PQ，已知点A的纵坐标为﹣2．
（1）求点A的横坐标；
（2）记四边形APQB的面积为S，若点B的横坐标为2，试用含k的代数式表示S．

【解答】解：（1）∵点A在函数y1＝（x＜0）的图象上，点A的纵坐标为﹣2，
∴﹣2＝，解得x＝﹣1，
∴点A的横坐标为﹣1；
（2）∵点B在函数y2＝（x＞0，k＞0）的图象上，点B的横坐标为2，
∴B（2，），
∴PC＝OQ＝，BQ＝2，
∵A（﹣1，﹣2），
∴OP＝CQ＝1，AP＝2，
∴AC＝2+，BC＝1+2＝3，
∴S＝S△ABC﹣S△PQC＝AC•BC﹣PC•CQ＝﹣×1＝3+k．
八．反比例函数与一次函数的交点问题（共1小题）
13．（2022•岳阳）如图，反比例函数y＝（k≠0）与正比例函数y＝mx（m≠0）的图象交于点A（﹣1，2）和点B，点C是点A关于y轴的对称点，连接AC，BC．
（1）求该反比例函数的解析式；
（2）求△ABC的面积；
（3）请结合函数图象，直接写出不等式＜mx的解集．

【解答】解：（1）把点A（﹣1，2）代入y＝（k≠0）得：2＝，
∴k＝﹣2，
∴反比例函数的解析式为y＝﹣；

（2）∵反比例函数y＝（k≠0）与正比例函数y＝mx（m≠0）的图象交于点A（﹣1，2）和点B，
∴B（1，﹣2），
∵点C是点A关于y轴的对称点，
∴C（1，2），
∴AC＝2，
∴S△ABC＝＝4．

（3）根据图象得：不等式＜mx的解集为x＜﹣1或0＜x＜1．
九．全等三角形的判定与性质（共2小题）
14．（2022•衡阳）如图，在△ABC中，AB＝AC，D、E是BC边上的点，且BD＝CE．求证：AD＝AE．

【解答】证明：∵AB＝AC，
∴∠B＝∠C，
在△ABD和△ACE中，
，
∴△ABD≌△ACE（SAS），
∴AD＝AE．
15．（2022•怀化）如图，在等边三角形ABC中，点M为AB边上任意一点，延长BC至点N，使CN＝AM，连接MN交AC于点P，MH⊥AC于点H．
（1）求证：MP＝NP；
（2）若AB＝a，求线段PH的长（结果用含a的代数式表示）．

【解答】（1）证明：过点M作MQ∥BC，交AC于点Q，如图所示：

在等边△ABC中，∠A＝∠B＝∠ACB＝60°，
∵MQ∥BC，
∴∠AMQ＝∠B＝60°，∠AQM＝∠ACB＝60°，∠QMP＝∠N，
∴△AMQ是等边三角形，
∴AM＝QM，
∵AM＝CN，
∴QM＝CN，
在△QMP和△CNP中，
，
∴△QMP≌△CNP（AAS），
∴MP＝NP；
（2）解：∵△AMQ是等边三角形，且MH⊥AC，
∴AH＝HQ，
∵△QMP≌△CNP，
∴QP＝CP，
∴PH＝HQ+QP＝AC，
∵AB＝a，AB＝AC，
∴PH＝a．
一十．平行四边形的判定与性质（共1小题）
16．（2022•株洲）如图所示，点E在四边形ABCD的边AD上，连接CE，并延长CE交BA的延长线于点F，已知AE＝DE，FE＝CE．
（1）求证：△AEF≌△DEC；
（2）若AD∥BC，求证：四边形ABCD为平行四边形．

【解答】证明：（1）在△AEF和△DEC中，
，
∴△AEF≌△DEC（SAS）；
（2）∵△AEF≌△DEC，
∴∠AFE＝∠DCE，
∴AB∥CD，
∵AD∥BC，
∴四边形ABCD为平行四边形．
一十一．正方形的判定（共1小题）
17．（2022•邵阳）如图，在菱形ABCD中，对角线AC，BD相交于点O，点E，F在对角线BD上，且BE＝DF，OE＝OA．
求证：四边形AECF是正方形．

【解答】证明：∵四边形ABCD是菱形，
∴AC⊥BD，OA＝OC，OB＝OD，
∵BE＝DF，
∴OE＝OF，
∴四边形AECF是菱形；
∵OE＝OA＝OF，
∴OE＝OF＝OA＝OC，即EF＝AC，
∴菱形AECF是正方形．
一十二．圆周角定理（共1小题）
18．（2022•怀化）如图，点A，B，C，D在⊙O上，＝．
求证：（1）AC＝BD；
（2）△ABE∽△DCE．

【解答】证明：（1）∵＝，
∴，
∴AC＝BD；
（2）∵∠A＝∠D，∠B＝∠C，
∴△ABE∽△DCE．
一十三．切线的性质（共1小题）
19．（2022•邵阳）如图，已知DC是⊙O的直径，点B为CD延长线上一点，AB是⊙O的切线，点A为切点，且AB＝AC．
（1）求∠ACB的度数；
（2）若⊙O的半径为3，求圆弧的长．

【解答】解：（1）连接OA，

∵AB是⊙O的切线，点A为切点，
∴∠BAO＝90°，
又∵AB＝AC，OA＝OC，
∴∠B＝∠ACB＝∠OAC，
设∠ACB＝x°，则在△ABC中，
x°+x°+x°+90°＝180°，
解得：x＝30，
∴∠ACB的度数为30°；
（2）∵∠ACB＝∠OAC＝30°，
∴∠AOC＝120°，
∴＝2π．
一十四．弧长的计算（共1小题）
20．（2022•湘潭）如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣1，1），B（﹣4，0），C（﹣2，2）．将△ABC绕原点O顺时针旋转90°后得到△A1B1C1．
（1）请写出A1、B1、C1三点的坐标：
A1　（1，1）　，B1　（0，4）　，C1　（2，2）　；
（2）求点B旋转到点B1的弧长．

【解答】解：（1）由图知，A1（1，1），B1（0，4），C1（2，2），
故答案为：（1，1），（0，4），（2，2）；
（2）由题意知，点B旋转到点B1的弧所在的圆的半径为4，弧所对的圆心角为90°，
∴弧长为：＝2π．
一十五．圆的综合题（共1小题）
21．（2022•永州）如图，已知AB，CE是⊙O的直径，BM是⊙O的切线，点D在EA的延长线上，AC，OD交于点F，∠MBC＝∠ACD．
（1）求证：∠MBC＝∠BAC；
（2）求证：AE＝AD；
（3）若△OFC的面积S1＝4，求四边形AOCD的面积S．

【解答】（1）证明：∵BM是⊙O的切线，
∴AB⊥BM，
∴∠ABC+∠MBC＝90°，
∵AB是⊙O的直径，
∴∠ACB＝90°，
∴∠ABC+∠BAC＝90°，
∴∠MBC＝∠BAC；
（2）证明：∵AO＝OC，
∴∠BAC＝∠ACE，
∵∠MBC＝∠ACD，∠MBC＝∠BAC，
∴∠ACD＝∠ACE，
∵CE是⊙O的直径，
∴∠EAC＝∠DAC＝90°，
∵AC＝AC，
∴△AEC≌△ADC（ASA），
∴AE＝AD；
（3）解：∵∠BAC＝∠ACD，
∴AB∥DC，
∴，
∴，
∴，
∵AO∥DC，
∴△AOF∽△CDF，
∴，
∵△OFC的面积S1＝4，
∴S△AOF＝2，S△ADF＝S△OCF＝4，S△CDF＝8，
∴S四边形AOCD＝S△AOF+S△ADF+S△CDF+S△COF＝2+4+8+4＝18．
一十六．轴对称-最短路线问题（共1小题）
22．（2022•永州）为提高耕地灌溉效率，小明的爸妈准备在耕地A、B、C、D四个位置安装四个自动喷洒装置（如图1所示），A、B、C、D四点恰好在边长为50米的正方形的四个顶点上，为了用水管将四个自动喷洒装置相互连通，爸妈设计了如下两个水管铺设方案（各图中实线为铺设的水管）．
方案一：如图2所示，沿正方形ABCD的三边铺设水管；
方案二：如图3所示，沿正方形ABCD的两条对角线铺设水管．
（1）请通过计算说明上述两方案中哪个方案铺设水管的总长度更短；
（2）小明看了爸妈的方案后，根据“蜂集原理”重新设计了一个方案（如图4所示）．

满足∠AEB＝∠CFD＝120°，AE＝BE＝CF＝DF，EF∥AD．请将小明的方案与爸妈的方案比较，判断谁的方案中铺设水管的总长度更短，并说明理由．（参考数据：≈1.4，≈1.7）

【解答】解：（1）方案一：铺设水管的总长度为50×3＝150（米），
方案二：铺设水管的总长度为2＝100≈140（米），
∵140＜150，
∴方案二铺设水管的总长度更短；
（2）小明的方案中铺设水管的总长度最短，理由如下：
如图：

∵AE＝BE，GE⊥AB，
∴AG＝BG＝AB＝25米，∠AEG＝∠BEG＝∠AEB＝60°，
同理DH＝CH＝25米，∠DFH＝∠CFH＝60°，
在Rt△AEG中，
GE＝＝（米），AE＝＝（米），
同理FH＝米，BE＝CF＝DF＝AE＝米
∴EF＝GH﹣GE﹣FH＝（50﹣）米，
∴方案中铺设水管的总长度为×4+50﹣＝50+50≈135（米），
∵135＜140＜150，
∴小明的方案中铺设水管的总长度最短．
一十七．相似三角形的判定与性质（共1小题）
23．（2022•常德）如图，已知AB是⊙O的直径，BC⊥AB于B，E是OA上的一点，ED∥BC交⊙O于D，OC∥AD，连接AC交ED于F．
（1）求证：CD是⊙O的切线；
（2）若AB＝8，AE＝1，求ED，EF的长．

【解答】（1）证明：连接OD，
∵AD∥OC，
∴∠BOC＝∠OAD，∠DOC＝∠ODA，
∵OA＝OD，
∴∠OAD＝∠ODA，
∴∠BOC＝∠DOC，
在△BOC和△DOC中，
，
∴△BOC≌△DOC（SAS），
∴∠ODC＝∠OBC＝90°，
∵OD为⊙O的半径，
∴CD是⊙O的切线；
（2）解：过点D作DH⊥BC于H，
∵ED∥BC，
∴∠OED＝180°﹣∠ABC＝90°，
则四边形EBHD为矩形，
∴BH＝ED，DH＝BE＝7，
∵AB＝8，AE＝1，
∴OE＝3，
∴ED＝＝＝，
∵CB、CD是⊙O的切线
∴CB＝CD，
设CB＝CD＝x，则CH＝x﹣，
在Rt△DHC中，DH2+CH2＝CD2，即72+（x﹣）2＝x2，
解得：x＝4，即BC＝4，
∵ED∥BC，
∴＝，即＝，
解得：EF＝．

一十八．特殊角的三角函数值（共1小题）
24．（2022•岳阳）计算：|﹣3|﹣2tan45°+（﹣1）2022﹣（﹣π）0．
【解答】解：|﹣3|﹣2tan45°+（﹣1）2022﹣（﹣π）0
＝3﹣2×1+1﹣1
＝3﹣2+1﹣1
＝1．
一十九．解直角三角形的应用-坡度坡角问题（共1小题）
25．（2022•株洲）如图（Ⅰ）所示，某登山运动爱好者由山坡①的山顶点A处沿线段AC至山谷点C处，再从点C处沿线段CB至山坡②的山顶点B处．如图（Ⅱ）所示，将直线l视为水平面，山坡①的坡角∠ACM＝30°，其高度AM为0.6千米，山坡②的坡度i＝1：1，BN⊥l于N，且CN＝千米．
（1）求∠ACB的度数；
（2）求在此过程中该登山运动爱好者走过的路程．
【解答】解：（1）∵山坡②的坡度i＝1：1，
∴CN＝BN，
∴∠BCN＝45°，
∴∠ACB＝180°﹣30°﹣45°＝105°；
（2）在Rt△ACM中，∠AMC＝90°，∠ACM＝30°，AM＝0.6千米，
∴AC＝2AM＝1.2千米，
在Rt△BCN中，∠BNC＝90°，∠BCN＝45°，CN＝千米，
则BC＝＝2（千米），
∴该登山运动爱好者走过的路程为：1.2+2＝3.2（千米），
答：该登山运动爱好者走过的路程为3.2千米．
二十．解直角三角形的应用-方向角问题（共1小题）
26．（2022•邵阳）如图，一艘轮船从点A处以30km/h的速度向正东方向航行，在A处测得灯塔C在北偏东60°方向上，继续航行1h到达B处，这时测得灯塔C在北偏东45°方向上，已知在灯塔C的四周40km内有暗礁，问这艘轮船继续向正东方向航行是否安全？并说明理由．（提示：≈1.414，≈1.732）

【解答】解：安全，理由如下：
过点C作CD垂直AB，

由题意可得，∠CAD＝90°﹣60°＝30°，∠CBD＝90°﹣45°＝45°，AB＝30×1＝30km，
在Rt△CBD中，设CD＝BD＝xkm，则AD＝（x+30）km，
在Rt△ACD中，tan30°＝，
∴，
∴，
解得：x＝15+15≈40.98＞40，
所以，这艘轮船继续向正东方向航行是安全的．
二十一．扇形统计图（共2小题）
27．（2022•湘潭）百年青春百年梦，初心献党向未来．为热烈庆祝中国共产主义青年团成立10周年，继承先烈遗志，传承“五四”精神．某中学在“做新时代好少年，强国有我”的系列活动中，开展了“好书伴我成长”的读书活动．为了解5月份八年级学生的读书情况，随机调查了八年级20名学生读书数量（单位：本），并进行了以下数据的整理与分析：
数据收集
2 5 3 5 4 6 1 5 3 4
3 6 7 5 8 3 4 7 3 4
数据整理
本数
0＜x≤2
2＜x≤4
4＜x≤6
6＜x≤8
组别
A
B
C
D
频数
2
m
6
3
数据分析 绘制成不完整的扇形统计图：
依据统计信息回答问题：
（1）在统计表中，m＝　9　；
（2）在扇形统计图中，C部分对应的圆心角的度数为 　108°　；
（3）若该校八年级学生人数为200人，请根据上述调查结果，估计该校八年级学生读书在4本以上的人数．

【解答】解：（1）由已知数据得B组的频数m＝20﹣（2+6+3）＝9，
故答案为：9；
（2）在扇形统计图中，C部分对应的圆心角的度数为360°×＝108°，
故答案为：108°；
（3）200×＝90（人），
答：估计该校八年级学生读书在4本以上的有90人．
28．（2022•怀化）电视剧《一代洪商》在中央电视台第八套播出后，怀化市各旅游景点知名度得到显著提高．为全面提高旅游服务质量，旅游管理部门随机抽取了100名游客进行满意度调查，并绘制成如下不完整的频数分布表和扇形统计图．
频数分布表
满意程度
频数（人）
频率
非常满意
50
0.5
满意
30
0.3
一般
a
c
不满意
b
0.05
合计
100
1
根据统计图表提供的信息，解答下列问题：
（1）a＝　15　，b＝　5　，c＝　0.15　；
（2）求扇形统计图中表示“一般”的扇形圆心角α的度数；
（3）根据调查情况，请你对各景点的服务提一至两条合理建议．

【解答】解：（1）由题意得，b＝100×0.05＝5，a＝100﹣50﹣30﹣5＝15，c＝1﹣0.5﹣0.3﹣0.05＝0.15，
故答案为：15；5；0.15；
（2）扇形统计图中表示“一般”的扇形圆心角α的度数为360°×0.15＝54°；
（3）在调查数据中，还有约20%的游客对服务态度表示“一般”或“不满意”，说明旅游质量还有待提高．（答案不唯一）．
二十二．条形统计图（共2小题）
29．（2022•常德）2020年7月，教育部印发的《大中小学劳动教育指导纲要（试行）》中明确要求中小学劳动教育课平均每周不少于1课时，初中生平均每周劳动时间不少于3小时．某初级中学为了解学生劳动教育的情况，从本校学生中随机抽取了500名进行问卷调查．如图是根据此次调查结果得到的统计图．
请根据统计图回答下列问题：
（1）本次调查中，平均每周劳动时间符合教育部要求的人数占被调查人数的百分比为多少？
（2）若该校有2000名学生，请估计最喜欢的劳动课程为木工的有多少人．
（3）请你根据本次问卷调查的结果给同学和学校各提一条合理化建议．

【解答】解：（1）×100%＝21%，
∴本次调查中，平均每周劳动时间符合教育部要求的人数占被调查人数的百分比为21%；
（2）2000×（1﹣40%﹣27%﹣7%﹣10%）＝320（人），
∴若该校有2000名学生，则最喜欢的劳动课程为木工的有320人；
（3）（答案不唯一，合理即可）
如：建议学生积极参加学校的劳动课程，多做家务等等；建议学校增设特色劳动课程，增加劳动课的课时等．
30．（2022•娄底）按国务院教育督导委员会办公室印发的《关于组织责任督学进行“五项管理”督导的通知》要求，各中小学校积极行动，取得了良好的成绩．某中学随机抽取了部分学生对他们一周的课外阅读时间（A：10h以上，B：8h～10h，C：6h～8h，D：6h以下）进行问卷调查，将所得数据进行分类，统计绘制了如下不完整的统计图．请根据图中的信息，解答下列问题：

（1）本次调查的学生共 　200　名；
（2）a＝　30　，b＝　50　；
（3）补全条形统计图．

【解答】解：（1）本次调查的学生共：10÷5%＝200（名），
故答案为：200；

（2）a＝×100＝30，b＝×100＝50，
故答案为：30，50；

（3）C类人数为200×15%＝30，
补全条形统计图如图：

二十三．列表法与树状图法（共2小题）
31．（2022•岳阳）守护好一江碧水，打造长江最美岸线．江豚，麋鹿，天鹅已成为岳阳“吉祥三宝”的新名片．某校生物兴趣小组设计了3张环保宣传卡片，正面图案如图所示，它们除此之外完全相同．
（1）将这3张卡片背面朝上，洗匀，从中随机抽取一张，则抽取的卡片正面图案恰好是“麋鹿”的概率为 　　；
（2）将这3张卡片背面朝上，洗匀，从中随机抽取一张，不放回，再从剩余的两张卡片中随机抽取一张，请用列表或画树状图的方法，求抽取的卡片正面图案恰好是“江豚”和“天鹅”的概率．

【解答】解：（1）将这3张卡片背面朝上，洗匀，从中随机抽取一张，
则抽取的卡片正面图案恰好是“麋鹿”的概率为，
故答案为：；
（2）将江豚，麋鹿，天鹅三张卡片分别记作①、②、③，
列表如下：

①
②
③
①

（②，①）
（③，①）
②
（①，②）

（③，②）
③
（①，③）
（②，③）

由表知，共有6种等可能结果，其中抽取的卡片正面图案恰好是“江豚”和“天鹅”的有2种结果，
所以抽取的卡片正面图案恰好是“江豚”和“天鹅”的概率为＝．
32．（2022•湘潭）5月30日是全国科技工作者日，某校准备举办“走近科技英雄，讲好中国故事”的主题比赛活动．八年级（一）班由A1、A2、A3三名同学在班上进行初赛，推荐排名前两位的同学参加学校决赛．
（1）请写出在班上初赛时，这三名同学讲故事顺序的所有可能结果；
（2）若A1、A2两名同学参加学校决赛，学校制作了编号为A、B、C的3张卡片（如图，除编号和内容外，其余完全相同），放在一个不透明的盒子里．先由A1随机摸取1张卡片记下编号，然后放回，再由A2随机摸取1张卡片记下编号，根据模取的卡片内容讲述相关英雄的故事．求A1、A2两人恰好讲述同一名科技英雄故事的概率（请用“画树状图”或“列表”等方法写出分析过程）．


【解答】解：（1）这三名同学讲故事的顺序是：A1、A2、A3；A1、A3、A2；A2、A1、A3；A2、A3、A1；A3、A1、A2；A3、A2、A1；共6种等可能的情况数；

（2）根据题意画图如下：

共有9种等可能的情况数，其中A1、A2两人恰好讲述同一名科技英雄故事的有3种，
则A1、A2两人恰好讲述同一名科技英雄故事的概率是＝．