贵州省各地区2022年中考数学真题按题型难易度分层分类汇编-03填空题（基础题）

这是一份贵州省各地区2022年中考数学真题按题型难易度分层分类汇编-03填空题（基础题），共23页。试卷主要包含了因式分解，分解因式，计算等内容，欢迎下载使用。
贵州省各地区2022年中考数学真题按题型难易度分层分类汇编-03填空题（基础题）
一．科学记数法—表示较小的数（共1小题）
1．（2022•黔东南州）有一种新冠病毒直径为0.000000012米，数0.000000012用科学记数法表示为 　 　．
二．非负数的性质：算术平方根（共1小题）
2．（2022•黔东南州）若（2x+y﹣5）2+＝0，则x﹣y的值是 　 　．
三．平方差公式（共1小题）
3．（2022•遵义）已知a+b＝4，a﹣b＝2，则a2﹣b2的值为 　 　．
四．因式分解-提公因式法（共1小题）
4．（2022•贵阳）因式分解：a2+2a＝　 　．
五．提公因式法与公式法的综合运用（共1小题）
5．（2022•黔东南州）分解因式：2022x2﹣4044x+2022＝　 　．
六．因式分解的应用（共1小题）
6．（2022•黔西南州）已知ab＝2，a+b＝3，求a2b+ab2的值是 　 　．
七．分式的加减法（共1小题）
7．（2022•黔西南州）计算：＝　 　．
八．方程的定义（共1小题）
8．（2022•贵阳）“方程”二字最早见于我国《九章算术》这部经典著作中，该书的第八章名为“方程”．如：从左到右列出的算筹数分别表示方程中未知数x，y的系数与相应的常数项，即可表示方程x+4y＝23，则表示的方程是 　 　．
九．解二元一次方程组（共1小题）
9．（2022•安顺）若a+2b＝8，3a+4b＝18，则a+b的值为　 　．
一十．根的判别式（共1小题）
10．（2022•铜仁市）若一元二次方程x2+2x+k＝0有两个相等的实数根，则k的值为 　 　．
一十一．解一元一次不等式组（共1小题）
11．（2022•铜仁市）不等式组的解集是 　 　．
一十二．规律型：点的坐标（共1小题）
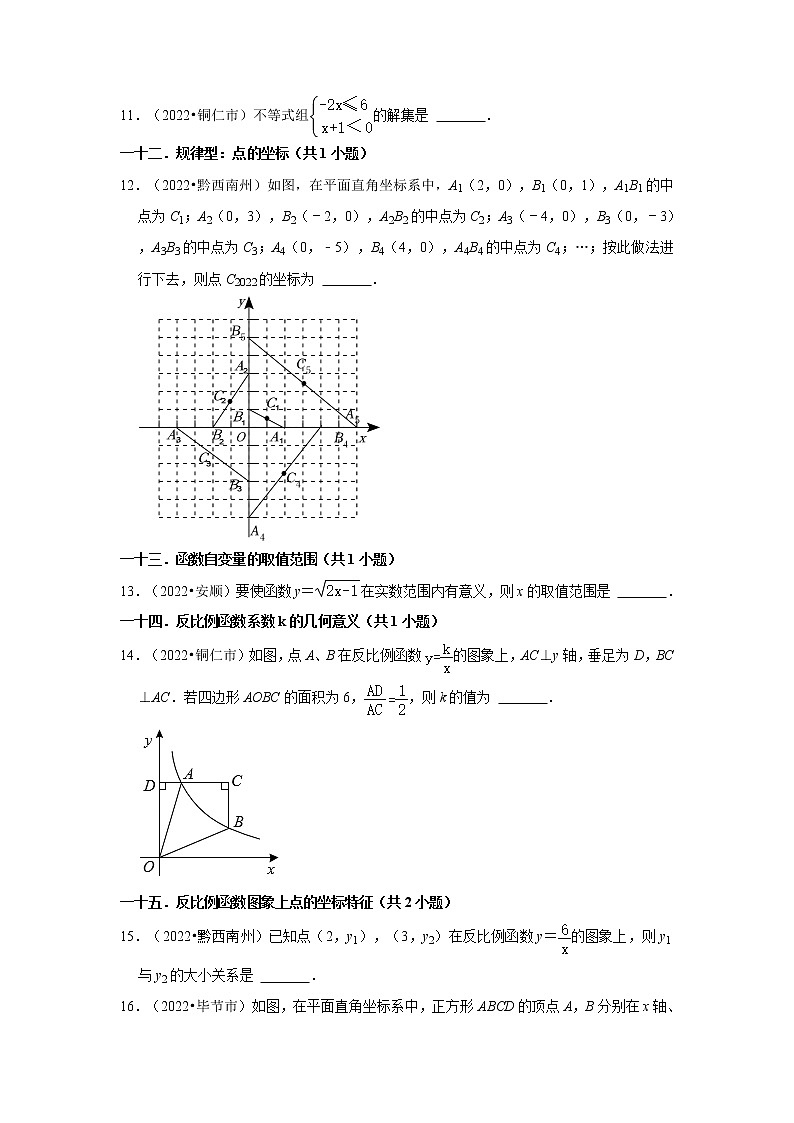
12．（2022•黔西南州）如图，在平面直角坐标系中，A1（2，0），B1（0，1），A1B1的中点为C1；A2（0，3），B2（﹣2，0），A2B2的中点为C2；A3（﹣4，0），B3（0，﹣3），A3B3的中点为C3；A4（0，﹣5），B4（4，0），A4B4的中点为C4；…；按此做法进行下去，则点C2022的坐标为 　 　．

一十三．函数自变量的取值范围（共1小题）
13．（2022•安顺）要使函数y＝在实数范围内有意义，则x的取值范围是 　 　．
一十四．反比例函数系数k的几何意义（共1小题）
14．（2022•铜仁市）如图，点A、B在反比例函数的图象上，AC⊥y轴，垂足为D，BC⊥AC．若四边形AOBC的面积为6，，则k的值为 　 　．

一十五．反比例函数图象上点的坐标特征（共2小题）
15．（2022•黔西南州）已知点（2，y1），（3，y2）在反比例函数y＝的图象上，则y1与y2的大小关系是 　 　．
16．（2022•毕节市）如图，在平面直角坐标系中，正方形ABCD的顶点A，B分别在x轴、y轴上，对角线交于点E，反比例函数y＝（x＞0，k＞0）的图象经过点C，E．若点A（3，0），则k的值是 　 　．

一十六．待定系数法求反比例函数解析式（共1小题）
17．（2022•黔东南州）如图，在平面直角坐标系中，等腰直角三角形ABC的斜边BC⊥x轴于点B，直角顶点A在y轴上，双曲线y＝（k≠0）经过AC边的中点D，若BC＝2，则k＝　 　．

一十七．反比例函数与一次函数的交点问题（共1小题）
18．（2022•遵义）反比例函数y＝（k≠0）与一次函数y＝x﹣1交于点A（3，n），则k的值为 　 　．
一十八．二次函数图象与几何变换（共1小题）
19．（2022•黔东南州）在平面直角坐标系中，将抛物线y＝x2+2x﹣1先绕原点旋转180°，再向下平移5个单位，所得到的抛物线的顶点坐标是 　 　．
一十九．二次函数的最值（共1小题）
20．（2022•六盘水）如图是二次函数y＝x2+bx+c的图象，该函数的最小值是 　 　．

二十．二次函数的应用（共1小题）
21．（2022•黔西南州）如图，是一名男生推铅球时，铅球行进过程中形成的抛物线．按照图中所示的平面直角坐标系，铅球行进高度y（单位：m）与水平距离x（单位：m）之间的关系是y＝﹣x2+x+，则铅球推出的水平距离OA的长是 　 　m．

二十一．等腰直角三角形（共1小题）
22．（2022•黔西南州）如图，在△ABC和△ADE中，∠BAC＝∠DAE＝90°，∠B＝60°，∠D＝45°，AC与DE相交于点F．若BC∥AE，则∠AFE的度数为 　 　．

二十二．平行四边形的性质（共1小题）
23．（2022•毕节市）如图，在Rt△ABC中，∠BAC＝90°，AB＝3，BC＝5，点P为BC边上任意一点，连接PA，以PA，PC为邻边作平行四边形PAQC，连接PQ，则PQ长度的最小值为 　 　．

二十三．菱形的性质（共1小题）
24．（2022•铜仁市）如图，四边形ABCD为菱形，∠ABC＝80°，延长BC到E，在∠DCE内作射线CM，使得∠ECM＝30°，过点D作DF⊥CM，垂足为F．若DF＝，则BD的长为 　 　（结果保留根号）．

二十四．垂径定理的应用（共1小题）
25．（2022•遵义）数学小组研究如下问题：遵义市某地的纬度约为北纬28°，求北纬28°纬线的长度．
小组成员查阅相关资料，得到如下信息：
信息一：如图1，在地球仪上，与赤道平行的圆圈叫做纬线；
信息二：如图2，赤道半径OA约为6400千米，弦BC∥OA，以BC为直径的圆的周长就是北纬28°纬线的长度；
（参考数据：π≈3，sin28°≈0.47，cos28°≈0.88，tan28°≈0.53）
根据以上信息，北纬28°纬线的长度约为 　 　千米．

二十五．旋转的性质（共1小题）
26．（2022•六盘水）如图，将△ABC绕点A旋转得到△ADE，若∠B＝90°，∠C＝30°，AB＝1，则AE＝　 　．

二十六．位似变换（共1小题）
27．（2022•黔西南州）如图，在平面直角坐标系中，△OAB与△OCD位似，位似中心是坐标原点O．若点A（4，0），点C（2，0），则△OAB与△OCD周长的比值是 　 　．

二十七．解直角三角形的应用-方向角问题（共1小题）
28．（2022•黔西南州）如图，我海军舰艇在某海域C岛附近巡航，计划从A岛向北偏东80°方向的B岛直线行驶．测得C岛在A岛的北偏东50°方向，在B岛的北偏西40°方向．A，B之间的距离为80nmile，则C岛到航线AB的最短距离约是 　 　nmile．（参考数据：≈1.4，≈1.7，保留整数结果）

二十八．中位数（共3小题）
29．（2022•黔东南州）某中学在一次田径运动会上，参加女子跳高的7名运动员的成绩如下（单位：m）：1.20，1.25，1.10，1.15，1.35，1.30，1.30．这组数据的中位数是 　 　．
30．（2022•黔西南州）某校九（1）班10名同学进行“引体向上”训练，将他们做的次数进行统计，制成下表，则这10名同学做的次数组成的一组数据中，中位数为 　 　．
次数
4
5
6
7
8
人数
2
3
2
2
1
31．（2022•铜仁市）一组数据3，5，8，7，5，8的中位数为 　 　．
二十九．随机事件（共1小题）
32．（2022•六盘水）将一副去掉大小王的扑克牌平均分发给甲、乙、丙、丁四人，已知甲有5张红桃牌，乙有4张红桃牌，那么丁的红桃牌有 　 　种不同的情况．
三十．概率公式（共1小题）
33．（2022•贵阳）端午节到了，小红煮好了10个粽子，其中有6个红枣粽子，4个绿豆粽子．小红想从煮好的粽子中随机捞一个，若每个粽子形状完全相同，被捞到的机会相等，则她捞到红枣粽子的概率是 　 　．
三十一．列表法与树状图法（共1小题）
34．（2022•毕节市）甲乙两人参加社会实践活动，随机选择“做环保志愿者”和“做交通引导员”两项中的一项，那么两人同时选择“做环保志愿者”的概率是 　 　．

贵州省各地区2022年中考数学真题按题型难易度分层分类汇编-03填空题（基础题）
参考答案与试题解析
一．科学记数法—表示较小的数（共1小题）
1．（2022•黔东南州）有一种新冠病毒直径为0.000000012米，数0.000000012用科学记数法表示为 　1.2×10﹣8　．
【解答】解：0.000000012＝1.2×10﹣8．
故答案为：1.2×10﹣8．
二．非负数的性质：算术平方根（共1小题）
2．（2022•黔东南州）若（2x+y﹣5）2+＝0，则x﹣y的值是 　9　．
【解答】解：根据题意可得，
，
由①﹣②得，
x﹣y＝9．
故答案为：9．
三．平方差公式（共1小题）
3．（2022•遵义）已知a+b＝4，a﹣b＝2，则a2﹣b2的值为 　8　．
【解答】解：∵a+b＝4，a﹣b＝2，
∴a2﹣b2＝（a+b）（a﹣b）
＝4×2
＝8，
故答案为：8．
四．因式分解-提公因式法（共1小题）
4．（2022•贵阳）因式分解：a2+2a＝　a（a+2）　．
【解答】解：a2+2a＝a（a+2）．
故答案为：a（a+2）．
五．提公因式法与公式法的综合运用（共1小题）
5．（2022•黔东南州）分解因式：2022x2﹣4044x+2022＝　2022（x﹣1）2　．
【解答】解：原式＝2022（x2﹣2x+1）
＝2022（x﹣1）2．
故答案为：2022（x﹣1）2．
六．因式分解的应用（共1小题）
6．（2022•黔西南州）已知ab＝2，a+b＝3，求a2b+ab2的值是 　6　．
【解答】解：a2b+ab2＝ab（a+b），
∵ab＝2，a+b＝3，
∴原式＝2×3＝6．
故答案为：6．
七．分式的加减法（共1小题）
7．（2022•黔西南州）计算：＝　1　．
【解答】解：原式＝
＝
＝1．
故答案为：1．
八．方程的定义（共1小题）
8．（2022•贵阳）“方程”二字最早见于我国《九章算术》这部经典著作中，该书的第八章名为“方程”．如：从左到右列出的算筹数分别表示方程中未知数x，y的系数与相应的常数项，即可表示方程x+4y＝23，则表示的方程是 　x+2y＝32　．
【解答】解：根据题知：从左到右列出的算筹数分别表示方程中未知数x，y的系数与相应的常数项，
一个竖线表示一个，一条横线表示一十，
所以该图表示的方程是：x+2y＝32．
九．解二元一次方程组（共1小题）
9．（2022•安顺）若a+2b＝8，3a+4b＝18，则a+b的值为　5　．
【解答】解：方法一、∵a+2b＝8，3a+4b＝18，
则a＝8﹣2b，
代入3a+4b＝18，
解得：b＝3，
则a＝2，
故a+b＝5．
方法二、∵a+2b＝8，3a+4b＝18，
∴2a+2b＝10，
∴a+b＝5，
故答案为：5．
一十．根的判别式（共1小题）
10．（2022•铜仁市）若一元二次方程x2+2x+k＝0有两个相等的实数根，则k的值为 　1　．
【解答】解：根据题意得Δ＝22﹣4×1×k＝0，即4﹣4k＝0
解得k＝1．
故答案为：1．
一十一．解一元一次不等式组（共1小题）
11．（2022•铜仁市）不等式组的解集是 　﹣3≤x＜﹣1　．
【解答】解：，
由①得：x≥﹣3，
由②得：x＜﹣1，
则不等式组的解集为﹣3≤x＜﹣1．
故答案为：﹣3≤x＜﹣1．
一十二．规律型：点的坐标（共1小题）
12．（2022•黔西南州）如图，在平面直角坐标系中，A1（2，0），B1（0，1），A1B1的中点为C1；A2（0，3），B2（﹣2，0），A2B2的中点为C2；A3（﹣4，0），B3（0，﹣3），A3B3的中点为C3；A4（0，﹣5），B4（4，0），A4B4的中点为C4；…；按此做法进行下去，则点C2022的坐标为 　（﹣1011，）　．

【解答】解：由题意可得，点∁n的位置按4次一周期的规律循环出现，
∵2022÷4＝505……2，
∴点C2022在第二象限，
∵位于第二象限内的点C2的坐标为（﹣1，），
点C6的坐标为（﹣3，），
点C10的坐标为（﹣5，），
……
∴点∁n的坐标为（﹣，），
∴当n＝2022时，﹣＝﹣＝﹣1011，＝＝，
∴点C2022的坐标为（﹣1011，），
故答案为：（﹣1011，）．
一十三．函数自变量的取值范围（共1小题）
13．（2022•安顺）要使函数y＝在实数范围内有意义，则x的取值范围是 　x≥　．
【解答】解：由题意得：2x﹣1≥0，
解得：x≥，
故答案为：x≥．
一十四．反比例函数系数k的几何意义（共1小题）
14．（2022•铜仁市）如图，点A、B在反比例函数的图象上，AC⊥y轴，垂足为D，BC⊥AC．若四边形AOBC的面积为6，，则k的值为 　3　．

【解答】解：设点，
∵AC⊥y轴，
∴AD＝a，，
∵，
∴AC＝2a，
∴CD＝3a，
∵BC⊥AC．AC⊥y轴，
∴BC∥y轴，
∴点B，
∴，
∵S梯形OBCD＝S△AOD+S四边形AOBC，
∴，
解得：k＝3．
故答案为：3．
一十五．反比例函数图象上点的坐标特征（共2小题）
15．（2022•黔西南州）已知点（2，y1），（3，y2）在反比例函数y＝的图象上，则y1与y2的大小关系是 　y1＞y2　．
【解答】解：∵反比例函数y＝中，k＝6＞0，
∴此函数图象的两个分支在一、三象限，
∵0＜2＜3，
∴两点都在第一象限，
∵在第一象限内y的值随x的增大而减小，
∴y1＞y2．
故答案为：y1＞y2．
16．（2022•毕节市）如图，在平面直角坐标系中，正方形ABCD的顶点A，B分别在x轴、y轴上，对角线交于点E，反比例函数y＝（x＞0，k＞0）的图象经过点C，E．若点A（3，0），则k的值是 　4　．

【解答】解：设C（m，），
∵四边形ABCD是正方形，
∴点E为AC的中点，
∴E（，），
∵点E在反比例函数y＝上，
∴，
∴m＝1，
作CH⊥y轴于H，

∴CH＝1，
∵四边形ABCD是正方形，
∴BA＝BC，∠ABC＝90°，
∴∠OBA＝∠HCB，
∵∠AOB＝∠BHC，
∴△AOB≌△BHC（AAS），
∴BH＝OA＝3，OB＝CH＝1，
∴C（1，4），
∴k＝4，
故答案为：4．
一十六．待定系数法求反比例函数解析式（共1小题）
17．（2022•黔东南州）如图，在平面直角坐标系中，等腰直角三角形ABC的斜边BC⊥x轴于点B，直角顶点A在y轴上，双曲线y＝（k≠0）经过AC边的中点D，若BC＝2，则k＝　﹣　．

【解答】解：如图，过点A作AE⊥BC于E，

∵等腰直角三角形ABC的斜边BC⊥x轴于点B，
∴CE＝BE，
∴AE＝BC＝，
∴A（0，），C（﹣，2），
∵D是AC的中点，
∴D（﹣，），
∴k＝﹣×＝﹣．
故答案为：﹣．
一十七．反比例函数与一次函数的交点问题（共1小题）
18．（2022•遵义）反比例函数y＝（k≠0）与一次函数y＝x﹣1交于点A（3，n），则k的值为 　6　．
【解答】解：∵一次函数y＝x﹣1经过点A（3，n），
∴n＝3﹣1＝2，
∵反比例函数y＝（k≠0）经过A（3，2）
∴k＝3×2＝6，
故答案为：6．
一十八．二次函数图象与几何变换（共1小题）
19．（2022•黔东南州）在平面直角坐标系中，将抛物线y＝x2+2x﹣1先绕原点旋转180°，再向下平移5个单位，所得到的抛物线的顶点坐标是 　（1，﹣3）　．
【解答】解：将抛物线y＝x2+2x﹣1绕原点旋转180°后所得抛物线为：﹣y＝（﹣x）2+2（﹣x）﹣1，即y＝﹣x2+2x+1，
再将抛物线y＝﹣x2+2x+1向下平移5个单位得y＝﹣x2+2x+1﹣5＝﹣x2+2x﹣4＝﹣（x﹣1）2﹣3，
∴所得到的抛物线的顶点坐标是（1，﹣3），
故答案为：（1，﹣3）．
一十九．二次函数的最值（共1小题）
20．（2022•六盘水）如图是二次函数y＝x2+bx+c的图象，该函数的最小值是 　﹣4　．

【解答】解：由函数图象可得：﹣＝﹣＝﹣1，
解得：b＝2，
∵图象经过（﹣3，0）点，
∴0＝（﹣3）2﹣3×2+c，
解得：c＝﹣3，
故二次函数解析式为：y＝x2+2x﹣3，
则二次函数的最小值为：＝＝﹣4．
故答案为：﹣4．
二十．二次函数的应用（共1小题）
21．（2022•黔西南州）如图，是一名男生推铅球时，铅球行进过程中形成的抛物线．按照图中所示的平面直角坐标系，铅球行进高度y（单位：m）与水平距离x（单位：m）之间的关系是y＝﹣x2+x+，则铅球推出的水平距离OA的长是 　10　m．

【解答】解：∵y＝﹣x2+x+，
∴当y＝0时，0＝﹣x2+x+，
解得x1＝﹣2，x2＝10，
∴OA＝10m，
故答案为：10．
二十一．等腰直角三角形（共1小题）
22．（2022•黔西南州）如图，在△ABC和△ADE中，∠BAC＝∠DAE＝90°，∠B＝60°，∠D＝45°，AC与DE相交于点F．若BC∥AE，则∠AFE的度数为 　105°　．

【解答】解：在△ABC和△ADE中，∠BAC＝∠DAE＝90°，∠B＝60°，∠D＝45°，
∴∠C＝180°﹣∠B﹣∠BAC＝30°，∠E＝180°﹣∠D﹣∠DAE＝45°，
∵BC∥AE，
∴∠CAE＝∠C＝30°，
在△AEF中，∠AFE＝180°﹣∠CAE﹣∠E＝105°．
故答案为：105°．
二十二．平行四边形的性质（共1小题）
23．（2022•毕节市）如图，在Rt△ABC中，∠BAC＝90°，AB＝3，BC＝5，点P为BC边上任意一点，连接PA，以PA，PC为邻边作平行四边形PAQC，连接PQ，则PQ长度的最小值为 　　．

【解答】解：∵∠BAC＝90°，AB＝3，BC＝5，
∴AC＝＝＝4，
∵四边形APCQ是平行四边形，
∴PO＝QO，CO＝AO＝2，
∵PQ最短也就是PO最短，
∴过O作BC的垂线OP′，

∵∠ACB＝∠P′CO，∠CP′O＝∠CAB＝90°，
∴△CAB∽△CP′O，
∴，
∴，
∴OP′＝，
∴则PQ的最小值为2OP′＝，
故答案为：．
二十三．菱形的性质（共1小题）
24．（2022•铜仁市）如图，四边形ABCD为菱形，∠ABC＝80°，延长BC到E，在∠DCE内作射线CM，使得∠ECM＝30°，过点D作DF⊥CM，垂足为F．若DF＝，则BD的长为 　2　（结果保留根号）．

【解答】解：如图，连接AC，交BD于点H，

由菱形的性质得∠ADC＝∠ABC＝80°，∠DCE＝80°，∠DHC＝90°，
又∵∠ECM＝30°，
∴∠DCF＝50°，
∵DF⊥CM，
∴∠CFD＝90°，
∴∠CDF＝40°，
又∵四边形ABCD是菱形，
∴BD平分∠ADC，
∴∠HDC＝40°，
在△CDH和△CDF中，
，
∴△CDH≌△CDF（AAS），
∴DH＝DF＝，
∴DB＝2DH＝．
故答案为：．
二十四．垂径定理的应用（共1小题）
25．（2022•遵义）数学小组研究如下问题：遵义市某地的纬度约为北纬28°，求北纬28°纬线的长度．
小组成员查阅相关资料，得到如下信息：
信息一：如图1，在地球仪上，与赤道平行的圆圈叫做纬线；
信息二：如图2，赤道半径OA约为6400千米，弦BC∥OA，以BC为直径的圆的周长就是北纬28°纬线的长度；
（参考数据：π≈3，sin28°≈0.47，cos28°≈0.88，tan28°≈0.53）
根据以上信息，北纬28°纬线的长度约为 　33792　千米．

【解答】解：作OK⊥BC，则∠BKO＝90°，
∵BC∥OA，∠AOB＝28°，
∵∠B＝∠AOB＝28°，
在Rt△BOK中，OB＝OA＝6400．
∴BK＝OB×cosB≈6400×0.88＝5632，
∴北纬28°的纬线长C＝2π•BK
≈2×3×5632
＝33792（千米）．
故答案为：33792．

二十五．旋转的性质（共1小题）
26．（2022•六盘水）如图，将△ABC绕点A旋转得到△ADE，若∠B＝90°，∠C＝30°，AB＝1，则AE＝　2　．

【解答】解：∵∠B＝90°，∠C＝30°，
∴AC＝2AB＝2，
∵将△ABC绕点A旋转得到△ADE，
∴AE＝AC＝2，
故答案为：2．
二十六．位似变换（共1小题）
27．（2022•黔西南州）如图，在平面直角坐标系中，△OAB与△OCD位似，位似中心是坐标原点O．若点A（4，0），点C（2，0），则△OAB与△OCD周长的比值是 　2　．

【解答】解：∵△OAB与△OCD位似，位似中心是坐标原点O，
而点A（4，0），点C（2，0），
∴相似比为4：2＝2：1，
∴△OAB与△OCD周长的比值为2．
故答案为：2．
二十七．解直角三角形的应用-方向角问题（共1小题）
28．（2022•黔西南州）如图，我海军舰艇在某海域C岛附近巡航，计划从A岛向北偏东80°方向的B岛直线行驶．测得C岛在A岛的北偏东50°方向，在B岛的北偏西40°方向．A，B之间的距离为80nmile，则C岛到航线AB的最短距离约是 　34　nmile．（参考数据：≈1.4，≈1.7，保留整数结果）

【解答】解：过点C作CF⊥AB于F，设CF＝xnmile．
由题意，得∠DAC＝50°，∠DAB＝80°，
∠CBE＝40°，AD∥BE，
则∠CAB＝∠DAB﹣∠DAC＝30°，
∵AD∥BE，
∴∠DAB+∠ABE＝180°，
∴∠ABE＝180°﹣∠DAB＝180°﹣80°＝100°，
∴∠ABC＝∠ABE﹣∠CBE＝100°﹣40°＝60°．
在Rt△ACF中，∵∠CAF＝30°，
∴AF＝CF＝x．
在Rt△CFB中，∵∠FBC＝60°，
∴BF＝CF＝x．
∵AF+BF＝AB，
∴x+x＝80，
解得x＝20≈34．
即C岛到航线AB的最短距离约为34nmile．
故答案为：34．

二十八．中位数（共3小题）
29．（2022•黔东南州）某中学在一次田径运动会上，参加女子跳高的7名运动员的成绩如下（单位：m）：1.20，1.25，1.10，1.15，1.35，1.30，1.30．这组数据的中位数是 　1.25　．
【解答】解：把这组数据从小到大排列：1.10，1.15，1.20，1.25，1.30，1.30，1.35．
所以这组数据的中位数为：1.25．
故答案为：1.25．
30．（2022•黔西南州）某校九（1）班10名同学进行“引体向上”训练，将他们做的次数进行统计，制成下表，则这10名同学做的次数组成的一组数据中，中位数为 　5.5　．
次数
4
5
6
7
8
人数
2
3
2
2
1
【解答】解：10名同学做的次数的中位数是＝5.5，
故答案为：5.5．
31．（2022•铜仁市）一组数据3，5，8，7，5，8的中位数为 　6　．
【解答】解：将题目中的数据按照从小到大的顺序排列为：3，5，5，7，8，8，位于最中间位置的两个数是5，7，故这组数据的中位数是．
故答案为：6．
二十九．随机事件（共1小题）
32．（2022•六盘水）将一副去掉大小王的扑克牌平均分发给甲、乙、丙、丁四人，已知甲有5张红桃牌，乙有4张红桃牌，那么丁的红桃牌有 　五　种不同的情况．
【解答】解：∵一副扑克牌有13张红桃牌，甲有5张红桃牌，乙有4张红桃牌，
∴剩余4张红桃牌，
∴丁的红桃牌有0，1，2，3，4张五种情况，
故答案为：五．
三十．概率公式（共1小题）
33．（2022•贵阳）端午节到了，小红煮好了10个粽子，其中有6个红枣粽子，4个绿豆粽子．小红想从煮好的粽子中随机捞一个，若每个粽子形状完全相同，被捞到的机会相等，则她捞到红枣粽子的概率是 　　．
【解答】解：∵共10个粽子，其中有6个红枣粽子，4个绿豆粽子，
∴P（捞到红枣馅粽子）＝＝，
故答案为：．
三十一．列表法与树状图法（共1小题）
34．（2022•毕节市）甲乙两人参加社会实践活动，随机选择“做环保志愿者”和“做交通引导员”两项中的一项，那么两人同时选择“做环保志愿者”的概率是 　　．
【解答】解：甲乙两人随机选择“做环保志愿者”和“做交通引导员”两项中的一项，所有可能出现的结果如下：

共有4种可能出现的结果，其中两人同时选择“做环保志愿者”的有1种，
所以两人同时选择“做环保志愿者”的概率为，
故答案为：．