湖北省各地区2022年中考数学真题按题型分层分类汇编-05填空题（提升题）

这是一份湖北省各地区2022年中考数学真题按题型分层分类汇编-05填空题（提升题），共19页。试卷主要包含了两点，且1＜m＜2， 　 　等内容，欢迎下载使用。
湖北省各地区2022年中考数学真题按题型分层分类汇编-05填空题（提升题）
一．反比例函数与一次函数的交点问题（共2小题）
1．（2022•鄂州）如图，已知直线y＝2x与双曲线y＝（k为大于零的常数，且x＞0）交于点A，若OA＝，则k的值为 　 　．

2．（2022•随州）如图，在平面直角坐标系中，直线y＝x+1与x轴，y轴分别交于点A，B，与反比例函数y＝的图象在第一象限交于点C，若AB＝BC，则k的值为 　 　．

二．二次函数的性质（共1小题）
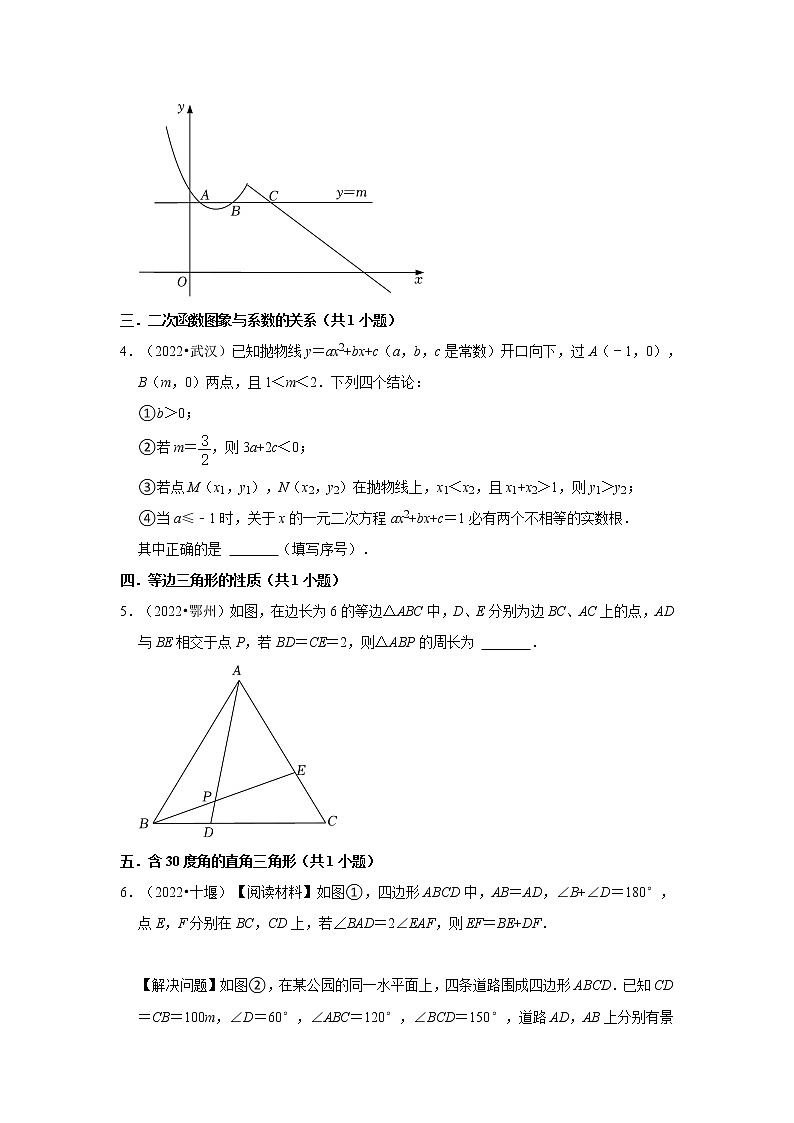
3．（2022•荆门）如图，函数y＝的图象由抛物线的一部分和一条射线组成，且与直线y＝m（m为常数）相交于三个不同的点A（x1，y1），B（x2，y2），C（x3，y3）（x1＜x2＜x3）．设t＝，则t的取值范围是 　 　．

三．二次函数图象与系数的关系（共1小题）
4．（2022•武汉）已知抛物线y＝ax2+bx+c（a，b，c是常数）开口向下，过A（﹣1，0），B（m，0）两点，且1＜m＜2．下列四个结论：
①b＞0；
②若m＝，则3a+2c＜0；
③若点M（x1，y1），N（x2，y2）在抛物线上，x1＜x2，且x1+x2＞1，则y1＞y2；
④当a≤﹣1时，关于x的一元二次方程ax2+bx+c＝1必有两个不相等的实数根．
其中正确的是 　 　（填写序号）．
四．等边三角形的性质（共1小题）
5．（2022•鄂州）如图，在边长为6的等边△ABC中，D、E分别为边BC、AC上的点，AD与BE相交于点P，若BD＝CE＝2，则△ABP的周长为 　 　．

五．含30度角的直角三角形（共1小题）
6．（2022•十堰）【阅读材料】如图①，四边形ABCD中，AB＝AD，∠B+∠D＝180°，点E，F分别在BC，CD上，若∠BAD＝2∠EAF，则EF＝BE+DF．

【解决问题】如图②，在某公园的同一水平面上，四条道路围成四边形ABCD．已知CD＝CB＝100m，∠D＝60°，∠ABC＝120°，∠BCD＝150°，道路AD，AB上分别有景点M，N，且DM＝100m，BN＝50（﹣1）m，若在M，N之间修一条直路，则路线M→N的长比路线M→A→N的长少 　 　m（结果取整数，参考数据：≈1.7）．

六．矩形的性质（共1小题）
7．（2022•十堰）“美丽乡村”建设使我市农村住宅旧貌变新颜，如图所示为一农村民居侧面截图，屋坡AF，AG分别架在墙体的点B，C处，且AB＝AC，侧面四边形BDEC为矩形．若测得∠FBD＝55°，则∠A＝　 　°．

七．切线的判定（共1小题）
8．（2022•湖北）如图，点P是⊙O上一点，AB是一条弦，点C是上一点，与点D关于AB对称，AD交⊙O于点E，CE与AB交于点F，且BD∥CE．给出下面四个结论：
①CD平分∠BCE；②BE＝BD；③AE2＝AF•AB；④BD为⊙O的切线．
其中所有正确结论的序号是 　 　．

八．三角形的内切圆与内心（共1小题）
9．（2022•恩施州）如图，在Rt△ABC中，∠C＝90°，AC＝4，BC＝3，⊙O为Rt△ABC的内切圆，则图中阴影部分的面积为（结果保留π） 　 　．

九．翻折变换（折叠问题）（共1小题）
10．（2022•十堰）如图，扇形AOB中，∠AOB＝90°，OA＝2，点C为OB上一点，将扇形AOB沿AC折叠，使点B的对应点B'落在射线AO上，则图中阴影部分的面积为 　 　．

一十．相似三角形的判定与性质（共1小题）
11．（2022•随州）如图1，在矩形ABCD中，AB＝8，AD＝6，E，F分别为AB，AD的中点，连接EF．如图2，将△AEF绕点A逆时针旋转角θ（0°＜θ＜90°），使EF⊥AD，连接BE并延长交DF于点H．则∠BHD的度数为 　 　，DH的长为 　 　．


一十一．解直角三角形的应用（共1小题）
12．（2022•荆门）如图，一艘海轮位于灯塔P的北偏东45°方向，距离灯塔100海里的A处，它沿正南方向以50海里/小时的速度航行t小时后，到达位于灯塔P的南偏东30°方向上的点B处，则t＝　 　小时．


湖北省各地区2022年中考数学真题按题型分层分类汇编-04填空题（提升题）
参考答案与试题解析
一．反比例函数与一次函数的交点问题（共2小题）
1．（2022•鄂州）如图，已知直线y＝2x与双曲线y＝（k为大于零的常数，且x＞0）交于点A，若OA＝，则k的值为 　2　．

【解答】解：设A（x，y），
∵点A在直线y＝2x上，且OA＝，
∴A点坐标为（ 1，2），
∵点A在双曲线y＝（x＞0）上，
∴2＝k，
故答案为：2．
2．（2022•随州）如图，在平面直角坐标系中，直线y＝x+1与x轴，y轴分别交于点A，B，与反比例函数y＝的图象在第一象限交于点C，若AB＝BC，则k的值为 　2　．

【解答】解：过点C作CH⊥x轴于点H．

∵直线y＝x+1与x轴，y轴分别交于点A，B，
∴A（﹣1，0），B（0，1），
∴OA＝OB＝1，
∵OB∥CH，
∴＝＝1，
∴OA＝OH＝1，
∴CH＝2OB＝2，
∴C（1，2），
∵点C在y＝上，
∴k＝2，
故答案为：2．
二．二次函数的性质（共1小题）
3．（2022•荆门）如图，函数y＝的图象由抛物线的一部分和一条射线组成，且与直线y＝m（m为常数）相交于三个不同的点A（x1，y1），B（x2，y2），C（x3，y3）（x1＜x2＜x3）．设t＝，则t的取值范围是 　＜t＜1　．

【解答】解：由二次函数y＝x2﹣2x+3（x＜2）可知：图象开口向上，对称轴为x＝1，
∴当x＝1时函数有最小值为2，x1+x2＝2，
由一次函数y＝﹣x+（x≥2）可知当x＝2时有最大值3，当y＝2时x＝，
∵直线y＝m（m为常数）相交于三个不同的点A（x1，y1），B（x2，y2），C（x3，y3）（x1＜x2＜x3），
∴y1＝y2＝y3＝m，2＜m＜3，
∴2＜x3＜，
∴t＝＝，
∴＜t＜1．
故答案为：＜t＜1．
三．二次函数图象与系数的关系（共1小题）
4．（2022•武汉）已知抛物线y＝ax2+bx+c（a，b，c是常数）开口向下，过A（﹣1，0），B（m，0）两点，且1＜m＜2．下列四个结论：
①b＞0；
②若m＝，则3a+2c＜0；
③若点M（x1，y1），N（x2，y2）在抛物线上，x1＜x2，且x1+x2＞1，则y1＞y2；
④当a≤﹣1时，关于x的一元二次方程ax2+bx+c＝1必有两个不相等的实数根．
其中正确的是 　①③④　（填写序号）．
【解答】解：∵对称轴x＝＞0，
∴对称轴在y轴右侧，
∴﹣＞0，
∵a＜0，
∴b＞0，
故①正确；
当m＝时，对称轴x＝﹣＝，
∴b＝﹣，
当x＝﹣1时，a﹣b+c＝0，
∴c＝0，
∴3a+2c＝0，故②错误；
由题意，抛物线的对称轴直线x＝h，0＜h＜0.5，
∵点M（x1，y1），N（x2，y2）在抛物线上，x1＜x2，且x1+x2＞1，
∴点M到对称轴的距离＜点N到对称轴的距离，
∴y1＞y2，故③正确；
设抛物线的解析式为y＝a（x+1）（x﹣m），
方程a（x+1）（x﹣m）＝1，
整理得，ax2+a（1﹣m）x﹣am﹣1＝0，
Δ＝[a（1﹣m）]2﹣4a（﹣am﹣1）
＝a2（m+1）2+4a，
∵1＜m＜2，a≤﹣1，
∴Δ＞0，
∴关于x的一元二次方程ax2+bx+c＝1必有两个不相等的实数根．故④正确，
故答案为：①③④．
四．等边三角形的性质（共1小题）
5．（2022•鄂州）如图，在边长为6的等边△ABC中，D、E分别为边BC、AC上的点，AD与BE相交于点P，若BD＝CE＝2，则△ABP的周长为 　　．

【解答】解：∵△ABC是等边三角形，
∴AB＝BC，∠ABD＝∠C＝60°，
在△ABD和△BCE中，

∴△ABD≌△BCE（SAS），
∴∠BAD＝∠CBE，
∴∠APE＝∠ABP+∠BAD＝∠ABP+∠CBE＝∠ABD＝60°，
∴∠APB＝120°，
在CB上取一点F使CF＝CE＝2，则BF＝BC﹣CF＝4，
∴∠C＝60°，
∴△CEF是等边三角形，
∴∠BFE＝120°，
即∠APB＝∠BFE，
∴△APB∽△BFE，
∴＝＝2，
设BP＝x，则AP＝2x，
作BH⊥AD延长线于H，

∵∠BPD＝∠APE＝60°，
∴∠PBH＝30°，
∴PH＝，BH＝，
∴AH＝AP+PH＝2x+＝x，
在Rt△ABH中，AH2+BH2＝AB2，
即（x）2+（x）2＝62，
解得x＝或﹣（舍去），
∴AP＝，BP＝，
∴△ABP的周长为AB+AP+BP＝6++＝6+＝，
故答案为：．
五．含30度角的直角三角形（共1小题）
6．（2022•十堰）【阅读材料】如图①，四边形ABCD中，AB＝AD，∠B+∠D＝180°，点E，F分别在BC，CD上，若∠BAD＝2∠EAF，则EF＝BE+DF．

【解决问题】如图②，在某公园的同一水平面上，四条道路围成四边形ABCD．已知CD＝CB＝100m，∠D＝60°，∠ABC＝120°，∠BCD＝150°，道路AD，AB上分别有景点M，N，且DM＝100m，BN＝50（﹣1）m，若在M，N之间修一条直路，则路线M→N的长比路线M→A→N的长少 　370　m（结果取整数，参考数据：≈1.7）．

【解答】解：解法一：如图，延长DC，AB交于点G，过点N作NH⊥AD于H，

∵∠D＝60°，∠ABC＝120°，∠BCD＝150°，
∴∠A＝360°﹣60°﹣120°﹣150°＝30°，
∴∠G＝90°，
∴AD＝2DG，
Rt△CGB中，∠BCG＝180°﹣150°＝30°，
∴BG＝BC＝50，CG＝50，
∴DG＝CD+CG＝100+50，
∴AD＝2DG＝200+100，AG＝DG＝150+100，
∵DM＝100，
∴AM＝AD﹣DM＝200+100﹣100＝100+100，
∵BG＝50，BN＝50（﹣1），
∴AN＝AG﹣BG﹣BN＝150+100﹣50﹣50（﹣1）＝150+50，
Rt△ANH中，∵∠A＝30°，
∴NH＝AN＝75+25，AH＝NH＝75+75，
由勾股定理得：MN＝＝＝50（+1），
∴AM+AN﹣MN＝100+100+150+50﹣50（+1）＝200+100≈370（m）．
答：路线M→N的长比路线M→A→N的长少370m．
解法二：如图，延长DC，AB交于点G，连接CN，CM，则∠G＝90°，

∵CD＝DM，∠D＝60°，
∴△BCM是等边三角形，
∴∠DCM＝60°，
由解法一可知：CG＝50，GN＝BG+BN＝50+50（﹣1）＝50，
∴△CGN是等腰直角三角形，
∴∠GCN＝45°，
∴∠BCN＝45°﹣30°＝15°，
∴∠MCN＝150°﹣60°﹣15°＝75°＝∠BCD，
由【阅读材料】的结论得：MN＝DM+BN＝100+50（﹣1）＝50+50，
∵AM+AN﹣MN＝100+100+150+50﹣50（+1）＝200+100≈370（m）．
答：路线M→N的长比路线M→A→N的长少370m．
故答案为：370．
六．矩形的性质（共1小题）
7．（2022•十堰）“美丽乡村”建设使我市农村住宅旧貌变新颜，如图所示为一农村民居侧面截图，屋坡AF，AG分别架在墙体的点B，C处，且AB＝AC，侧面四边形BDEC为矩形．若测得∠FBD＝55°，则∠A＝　110　°．

【解答】解：∵四边形BDEC为矩形，
∴∠DBC＝90°，
∵∠FBD＝55°，
∴∠ABC＝180°﹣∠DBC﹣∠FBD＝35°，
∵AB＝AC，
∴∠ABC＝∠ACB＝35°，
∴∠A＝180°﹣∠ABC﹣∠ACB＝110°，
故答案为：110．
七．切线的判定（共1小题）
8．（2022•湖北）如图，点P是⊙O上一点，AB是一条弦，点C是上一点，与点D关于AB对称，AD交⊙O于点E，CE与AB交于点F，且BD∥CE．给出下面四个结论：
①CD平分∠BCE；②BE＝BD；③AE2＝AF•AB；④BD为⊙O的切线．
其中所有正确结论的序号是 　①②④　．

【解答】解：∵点C与点D关于AB对称，
∴AB是CD的垂直平分线，
∴AD＝AC，BD＝BC，
∴∠BCD＝∠BDC，
∵BD∥CE，
∴∠BDC＝∠DCE，
∴∠DCE＝∠BCD，
∴CD平分∠BCE；
故①正确；
∵四边形ACBE是⊙O的内接四边形，
∴∠ACB+∠AEB＝180°，
∵∠AEB+∠DEB＝180°，
∴∠DEB＝∠ACB，
∵AD＝AC，BD＝BC，AB＝AB，
∴△ADB≌△ACB（SSS），
∴∠ADB＝∠ACB，
∴∠DEB＝∠ADB，
∴BD＝BE，
故②正确；
∵AC≠AE，
∴≠，
∴∠AEF≠∠ABE，
∴△AEF与△ABE不相似，
故③不正确；
连接OB，交EC于点H，

∵BD＝BE，BD＝BC，
∴BE＝BC，
∴＝，
∴OB⊥CE，
∴∠OHE＝90°，
∵BD∥CE，
∴∠OHE＝∠OBD＝90°，
∵OB是⊙O的半径，
∴BD为⊙O的切线，
故④正确；
所以给出上面四个结论，其中所有正确结论的序号是：①②④，
故答案为：①②④．

八．三角形的内切圆与内心（共1小题）
9．（2022•恩施州）如图，在Rt△ABC中，∠C＝90°，AC＝4，BC＝3，⊙O为Rt△ABC的内切圆，则图中阴影部分的面积为（结果保留π） 　5﹣π　．

【解答】解：作OD⊥AC于点D，作OE⊥CB于点E，作OF⊥AB于点F，连接OA、OC、OB，如图，
∵∠C＝90°，OD＝OE＝OF，
∴四边形CEOD是正方形，
∵AC＝4，BC＝3，∠C＝90°，
∴AB＝＝＝5，
∵S△ABC＝S△AOC+S△COB+S△BOA，
∴＝，
解得OD＝OE＝OF＝1，
∴图中阴影部分的面积为：﹣1×1﹣π×12×＝5﹣π，
故答案为：5﹣π．

九．翻折变换（折叠问题）（共1小题）
10．（2022•十堰）如图，扇形AOB中，∠AOB＝90°，OA＝2，点C为OB上一点，将扇形AOB沿AC折叠，使点B的对应点B'落在射线AO上，则图中阴影部分的面积为 　π+4﹣4　．

【解答】解：连接AB，
∵∠AOB＝90°，OA＝2，
∴OB＝OA＝2，
∴AB＝＝2，
设OC＝x，则BC＝B′C＝2﹣x，OB′＝2﹣2，
则x2+（2﹣2）2＝（2﹣x）2，
解得x＝2﹣2，
∴阴影部分的面积是：＝π+4﹣4，
故答案为：π+4﹣4．

一十．相似三角形的判定与性质（共1小题）
11．（2022•随州）如图1，在矩形ABCD中，AB＝8，AD＝6，E，F分别为AB，AD的中点，连接EF．如图2，将△AEF绕点A逆时针旋转角θ（0°＜θ＜90°），使EF⊥AD，连接BE并延长交DF于点H．则∠BHD的度数为 　90°　，DH的长为 　　．


【解答】解：如图，设EF交AD于点J，AD交BH于点O，过点E作EK⊥AB于点K．

∵∠EAF＝∠BAD＝90°，
∴∠DAF＝∠BAE，
∵＝＝，
∴＝，
∴△DAF∽△BAE，
∴∠ADF＝∠ABE，
∵∠DOH＝∠AOB，
∴∠DHO＝∠BAO＝90°，
∴∠BHD＝90°，
∵AF＝3，AE＝4，∠EAF＝90°，
∴EF＝＝5，
∵EF⊥AD，
∴•AE•AF＝•EF•AJ，
∴AJ＝，
∴EJ＝＝＝，
∵EJ∥AB，
∴＝，
∴＝，
∴OJ＝，
∴OA＝AJ+OJ＝+＝4，
∴OB＝＝＝4，OD＝AD﹣AO＝6﹣4＝2，
∵cos∠ODH＝cos∠ABO，
∴＝，
∴＝，
∴DH＝．
故答案为：90°，．
一十一．解直角三角形的应用（共1小题）
12．（2022•荆门）如图，一艘海轮位于灯塔P的北偏东45°方向，距离灯塔100海里的A处，它沿正南方向以50海里/小时的速度航行t小时后，到达位于灯塔P的南偏东30°方向上的点B处，则t＝　（1+）　小时．

【解答】解：如图：

由题意得：
∠PAC＝45°，∠PBA＝30°，AP＝100海里，
在Rt△APC中，AC＝AP•cos45°＝100×＝50（海里），
PC＝AP•sin45°＝100×＝50（海里），
在Rt△BCP中，BC＝＝＝50（海里），
∴AB＝AC+BC＝（50+50）海里，
∴t＝＝（1+）小时，
故答案为：（1+）．