2021-2022学年江西省吉安市遂川县七年级（下）期末数学试卷（Word解析版）

这是一份2021-2022学年江西省吉安市遂川县七年级（下）期末数学试卷（Word解析版），共16页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。
2021-2022学年江西省吉安市遂川县七年级（下）期末数学试卷 题号一二三四总分得分       一、选择题（本大题共6小题，共18分。在每小题列出的选项中，选出符合题目的一项）计算所得结果为(    )A.  B.  C.  D. 下列是北京大学、中国科学院大学、中国药科大学和中南大学的标志中的图案，其中是中心对称图形的有(    )
A. 个 B. 个 C. 个 D. 个如图所示，在所标识的角中，内错角是(    )A. 和
B. 和
C. 和
D. 和下列不能用平方差公式计算的是(    )A.  B.
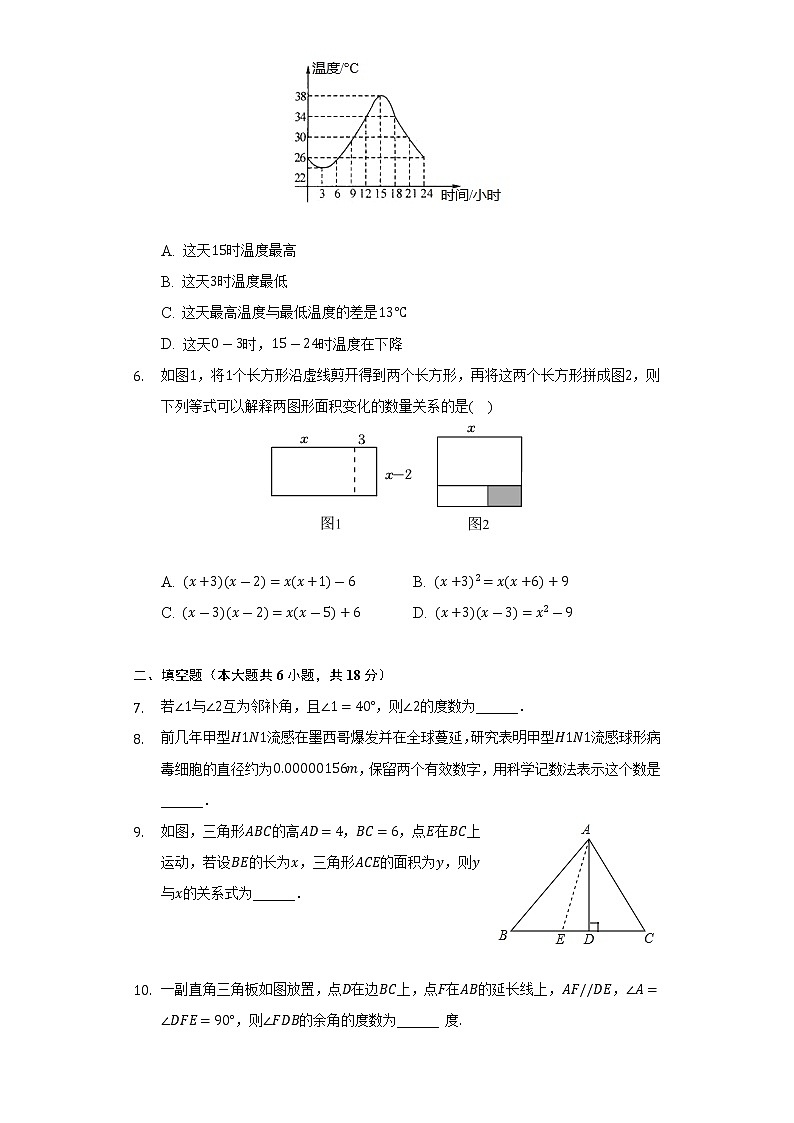
C.  D. 如图所示是某市夏天的温度随时间变化的图象，通过观察可知，下列说法中错误的是(    )
A. 这天时温度最高
B. 这天时温度最低
C. 这天最高温度与最低温度的差是
D. 这天时，时温度在下降如图，将个长方形沿虚线剪开得到两个长方形，再将这两个长方形拼成图，则下列等式可以解释两图形面积变化的数量关系的是(    )
A.  B.
C.  D.  二、填空题（本大题共6小题，共18分）若与互为邻补角，且，则的度数为______．前几年甲型流感在墨西哥爆发并在全球蔓延，研究表明甲型流感球形病毒细胞的直径约为，保留两个有效数字，用科学记数法表示这个数是______．如图，三角形的高，，点在上运动，若设的长为，三角形的面积为，则与的关系式为______．
 一副直角三角板如图放置，点在边上，点在的延长线上，，，则的余角的度数为______ 度
若，，则 ______ ．如图，一副三角板的两个直角顶点重合，已知，，则当的一边与的一边平行或重合，且点在的左侧时，小于平角的度数为______．
  三、计算题（本大题共1小题，共6分）计算：；
如图所示，，，比大，求的度数．
  四、解答题（本大题共10小题，共78分。解答应写出文字说明，证明过程或演算步骤）为了有效提高人民免疫水平，最终阻断病毒传染，某地接种新冠疫苗，已知每天可接种人．
直接写出接种人数与时间天之间的函数关系式；
如果计划接种万人，则需要多天才能完成接种任务？先化简，再求值：，其中，．一不透明的布袋里，装有红、黄、蓝三种颜色的小球除颜色外其余都相同，其中有红球个，蓝球个，黄球若干个，现从中任意摸出个球是红球的概率为．
求口袋中黄球的个数；
现规定：摸到红球得分，摸到黄球得分，摸到蓝球得分每次摸后放回，乙同学在一次摸球游戏中，第一次随机摸到一个红球第二次又随机摸到一个蓝球，若随机再摸一次，求乙同学三次摸球所得分数之和不低于分的概率．如图，在所标注的角中．
对顶角有______对，邻补角有______对；
若，，求与的度数．
某公交车每月的支出费用为元，每月的乘车人数人与每月利润利润收入费用支出费用元的变化关系如下表所示每位乘客的公交票价是固定不变的：人元在这个变化过程中，______是自变量，______是因变量；
观察表中数据可知，每月乘客量达到______人以上时，该公交车才不会亏损；
请你估计当每月乘车人数为人时，每月利润为多少元？把推理过程补充完整，并填写相应的理由．
如图，已知，
______
______
又平分已知，
____________
__________________
______
小明家所在的小区有一个池塘，如图，、两点分别位于一个池塘的两侧，池塘西边有一座假山，在的中点处有一个雕塑，小明从出发，沿直线一直向前经过点走到点，并使，然后他测量点到假山的距离，则的长度就是、两点之间的距离．
你能说明小明这样做的根据吗？
如果小明未带测量工具，但是知道和假山、雕塑分别相距米、米，你能帮助他确定的长度范围吗？
如图，将两个长方形用不同方式拼成图和图两个图形．
若图中的阴影部分面积为，则图中的阴影部分面积为______用含字母，的代数式表示；
由你可以得到的等式是______；
根据你所得到的等式解决下面的问题：
若，，则______；
计算：．
 
观察下列运算过程：
，；
，；
根据以上运算过程和结果，我们发现：______；______；
仿照中的规律，判断与的大小关系；
求的值．如图，在中，，，，过点作射线，且，点从点出发，沿射线方向匀速运动，速度为；点从点出发，沿边向点匀速运动，速度为，当点停止运动时，点也停止运动连接，，设动点的运动时间为，解答下列问题：
用含有的代数式表示和的长度；
当时，请说明；
设的面积为，求与之间的关系式．

答案和解析 1.【答案】 【解析】解：原式

．
故选：．
先算乘方，再算乘法．
本题考查同底数幂的乘法，确定运算顺序，掌握运算法则是求解本题的关键．
 2.【答案】 【解析】解：左起第一、第三、第四个图形都不能找到这样的一个点，使这些图形绕某一点旋转与原来的图形重合，所以不是中心对称图形；
第二个图形能找到这样的一个点，使这个图形绕某一点旋转与原来的图形重合，所以是中心对称图形；
所以是中心对称图形的有个．
故选：．
一个图形绕某一点旋转，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形．根据中心对称图形的概念对各选项分析判断即可得解．
本题考查了中心对称图形的概念，中心对称图形是要寻找对称中心，旋转度后与原图重合．
 3.【答案】 【解析】解：根据内错角的定义得和不是内错角，和是内错角，和是同位角，和不是内错角．
故选：．
根据同位角、内错角、同旁内角的定义解答即可．
本题主要考查了同位角、内错角、同旁内角，解题的关键是熟记同位角、内错角、同旁内角的定义．
 4.【答案】 【解析】解：、符合平方差公式的结构特点，能运用平方差公式计算；
B.，不符合平方差公式的结构特点，不能运用平方差公式计算；
D.符合平方差公式的结构特点，能运用平方差公式计算．
故选：．
根据“两个数的和与两个数的差的积”能运用平方差公式，逐个分析得结论．
本题考查了平方差公式，掌握平方差公式的结构特点是解决本题的关键．
 5.【答案】 【解析】解：横轴表示时间，纵轴表示温度．
温度最高应找到图象的最高点所对应的值：为点，对；
温度最低应找到图象的最低点所对应的值：为时，对；
这天最高温度与最低温度的差应让前面的两个值相减，即，错；
从图象看出，这天时，时温度在下降，对．
故选C．
根据图象的信息，逐一判断即可．
此题考查了用图象表示变量之间的关系，运用了数形结合思想，会根据所给条件找到对应的纵轴表示的数是本题的关键．
 6.【答案】 【解析】解：图为长是，宽为的长方形，因此面积为，
图中阴影部分是长为，宽为的长方形，因此阴影部分的面积为，整体是长为，宽为的长方形，因此面积为，
所以空白部分的面积为，
于是有，
故选：．
分别用代数式表示图、图的面积即可．
本题考查平方差公式的几何背景，完全平方公式的几何背景以及多项式乘多项式，掌握完全平方公式、平方差公式的结构特征以及多项式乘多项式的计算法则是正确解答的前提．
 7.【答案】 【解析】解：由题意得，．
，
．
故答案为：．
根据邻补角的定义解决此题．
本题主要考查邻补角，熟练掌握邻补角的定义是解决本题的关键．
 8.【答案】 【解析】解：
故答案为：
用科学记数法表示该数，先根据有效数字的概念保留两个有效数字为，再确定的指数为，指数由原数左边起第一个不为零的数字前面的的个数所决定．
本题考查用科学记数法表示较小的数，一般形式为，其中，为由原数左边起第一个不为零的数字前面的的个数所决定．此题还要注意保留有效数字．
 9.【答案】 【解析】解：由线段的和差，得，
由三角形的面积，得
，
化简，得，
故答案为：．
根据线段的和差，可得的长，根据三角形的面积，可得答案．
本题考查了函数关系式，利用三角形的面积公式是解题关键．
 10.【答案】 【解析】解：，
，
，
，
解得：，
的余角的度数为．
故答案为：．
直接利用三角板的内角度数以及平行线的性质得出，再利用三角形外角的性质得出答案．
此题主要考查了平行线的性质，正确掌握平行线的性质是解题关键．
 11.【答案】 【解析】解：，，




．
故答案为：．
根据完全平方公式可得，再把相应数值代入计算即可．
本题主要考查了完全平方公式，熟记公式是解答本题的关键．
 12.【答案】或 【解析】解：当的一边与的一边平行或重合，且点在的左侧时．
符合条件的情况有两种：；．
当时，如图所示，

，
．

．
．
．
当时，
，
．
，
．
．
故答案为：或．
根据题意得，应分为与两种情况进行求解，然后利用平行线的性质求出有关角的度数．
本题考查了平行线的性质与三角形内角和定理，解题的关键是根据已知条件得出两种可能的情况．
 13.【答案】解：原式；
，，比大，
，，
，
，
，
，
． 【解析】运用整式的除法法则即可运算；
根据题意解出各角度数，即可得出答案．
本题考查了实数的运算，角的运算，解题关键在于正确的计算．
 14.【答案】解：依据题意得：；
依据题意得：，
解得：，
答：需要天才能完成接种任务． 【解析】根据总人数等于天数乘以每天人均接种疫苗人数得出结论；
把总人数代入中关系式求解．
本题考查了一次函数的应用，理解题意列出关系式是解题的关键．
 15.【答案】解：原式

，
当，时，原式． 【解析】本题考查的是整式的化简求出，熟知整式混合运算的法则是解答此题的关键．
先根据整式混合运算的法则把原式进行化简，再把，代入进行计算即可．
 16.【答案】解：，
，
故有黄球个；
，
所以第三次摸球得分应不低于分，
故应该摸到黄球或者红球，
所以概率为：． 【解析】根据简单事件的概率公式求解；
先推算积分，再求概率．
主要考查了事件概率的求法．简单事件的概率公式是解题的关键．
 17.【答案】   【解析】解：图中的对顶角有与，与共对，
邻补角有：与，与，与，与，与，与，共对，
故答案为：，；
，，
，
又，
；
，
答：，．
根据对顶角、邻补角的定义结合具体的图形进行判断即可；
利用角的和差关系，邻补角的定义进行计算即可．
本题考查对顶角、邻补角，掌握对顶角相等以及邻补角的定义是正确解答的前提．
 18.【答案】解：每月的乘车人数，每月的利润；
观察表中数据可知，每月乘客量达到；
由表中数据可知，每月的乘车人数每增加人，每月的利润可增加元，
当每月的乘车人数为人时，每月利润为元，则当每月乘车人数为人时，每月利润为元． 【解析】解：在这个变化过程中，每月的乘车人数是自变量，每月的利润是因变量；
故答案为：每月的乘车人数，每月的利润；
观察表中数据可知，每月乘客量达到观察表中数据可知，每月乘客量达到人以上时，该公交车才不会亏损；
故答案为：观察表中数据可知，每月乘客量达到；
见答案．
【解析】
直接利用常量与变量的定义分析得出答案；
直接利用表中数据分析得出答案；
利用由表中数据可知，每月的乘车人数每增加人，每月的利润可增加元，进而得出答案．
此题主要考查了常量与变量以及变量之间的关系，正确把握函数的定义是解题关键．
 19.【答案】两直线平行，内错角相等  两直线平行，同位角相等    角平分线的定义      等量代换  等量代换 【解析】证明：已知，
两直线平行，内错角相等，
两直线平行，同位角相等，
又平分已知，
角平分线的定义，
等量代换，
等量代换．
故答案为：两直线平行，内错角相等；两直线平行，同位角相等；；角平分线的定义；；；等量代换；等量代换．
已知，利用平行线的性质可得，，根据角平分线的性质可得，然后等量代换证得结论．
本题考查了平行线的判定和性质，熟练应用判定定理和性质定理是解题的关键，平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．平行线的判定是由角的数量关系判断两直线的位置关系．平行线的性质是由平行关系来寻找角的数量关系．应用平行线的判定和性质定理时，一定要弄清题设和结论，切莫混淆．
 20.【答案】解：证明：在和中
，
≌，
；

如图，连接，
米，米，
米，
米米，
米米． 【解析】利用两边切夹角相等的两三角形全等，即可得出答案；
利用，得出米，再利用即可得出答案．
此题主要考查了全等三角形的判定与性质，根据已知得出≌是解题关键．
 21.【答案】     【解析】解：图是长为，宽为的长方形，因此面积为，
故答案为：；
由图、图中阴影部分的面积相等得，，
故答案为：；
，即，而，
，
故答案为：；
原式

．
根据图，用代数式表示其长、宽，利用面积公式可得答案；
由图、图的面积相等可得答案；
利用的结论，即平方差公式进行计算即可；
利用平方差公式进行计算即可．
本题考查平方差公式的几何背景，掌握平方差公式的结构特征是正确解答的前提．
 22.【答案】  【解析】解：，，
；
，，
，
故答案为：；；
，理由：
，
，
．
原式


．
观察计算过程即可得出结论；
利用题干中的方法解答即可得出结论；
利用以上的解题规律进行运算即可．
本题主要考查了有理数的混合运算，本题是阅读型题目，利用题干中的方法和解答中发现的规律解答是解题的关键．
 23.【答案】解：点从点出发，沿射线方向匀速运动，速度为；
，
点从点出发，沿边向点匀速运动，速度为，
，
；
当时，，，
，
，
，
在和中，
，
≌，
，
；
如图，过点作于，

，，，，
，
，
与之间的关系式． 【解析】由路程速度时间，可求解；
由“”可证≌，可得，可得结论；
过点作于，由等腰直角三角形的性质可求，由三角形的面积公式可求解．
本题是三角形综合题，考查了全等三角形的判定和性质，等腰直角三角形的性质，灵活运用这些性质解决问题是本题的关键．