初中数学人教版八年级上册第十一章 三角形综合与测试单元测试同步测试题

这是一份初中数学人教版八年级上册第十一章 三角形综合与测试单元测试同步测试题，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题
1. 如图，∠1=20∘，∠2=25∘，∠A=35∘，则 ∠D 的度数为
A. 60∘B. 70∘C. 80∘D. 无法确定

2. 如图，∠CGE=α，则 ∠A+∠B+∠C+∠D+∠E+∠F 的度数为
A. 360∘-αB. 270∘-αC. 180∘+αD. 2α

3. 如图，∠1+∠2+∠3+∠4 的度数为
A. 180∘B. 270∘C. 360∘D. 540∘

4. 如图，BE 是 ∠ABD 的平分线，CF 是 ∠ACD 的平分线，BE，CF 相交于点 G．若 ∠BDC=140∘，∠BGC=110∘，则 ∠A 的度数是
A. 70∘B. 75∘C. 80∘D. 85∘

二、填空题
5. 将一副直角三角尺按如图所示的方式摆放，点 C 在 EF 上，AC 经过点 D．已知 ∠A=∠EDF=90∘，AB=AC，∠E=30∘，∠BCE=40∘，则 ∠CDF= ．

6. 如图，在 △ABC 中，∠B=∠C，FD⊥BC，DE⊥AB，∠AFD=158∘，则 ∠EDF= ．

7. 如图，∠A+∠B+∠C+∠D+∠E= ．

8. 如图，M 是 △ABC 两个内角平分线的交点，N 是 △ABC 两个外角平分线的交点．如果 ∠CMB:∠CNB=3:2，那么 ∠CAB= ．

三、解答题
9. 如图①，在 △ABC 中，AD⊥BC 于点 D，CE⊥AB 于点 E．
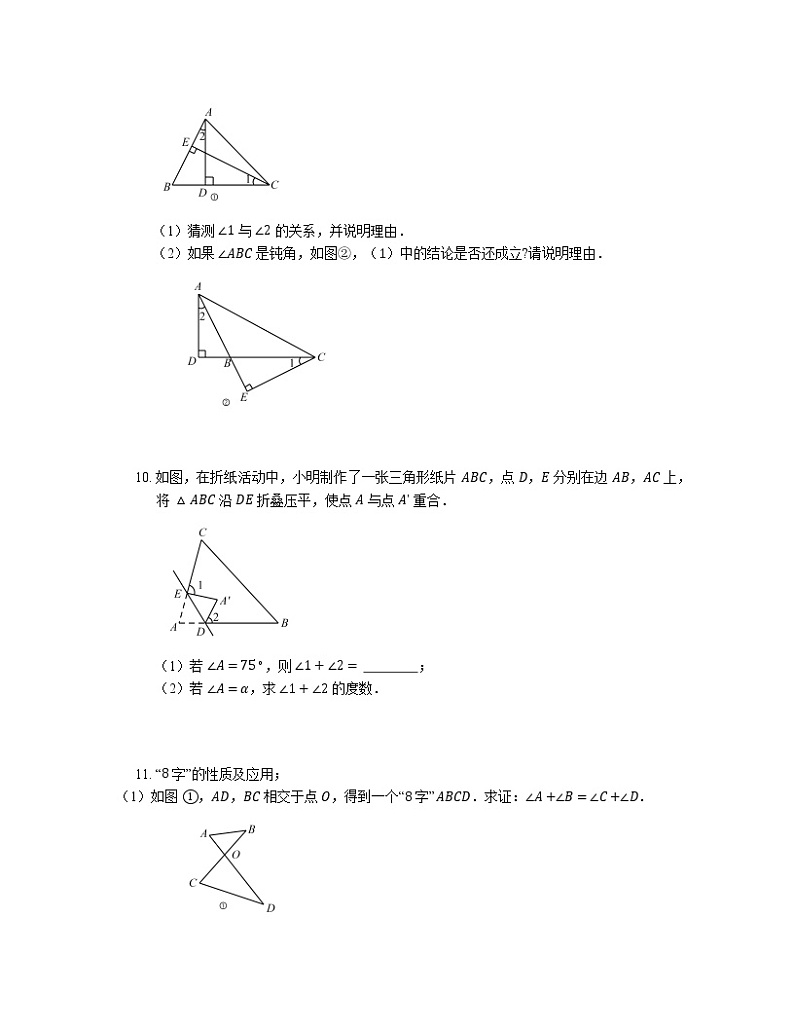
（1）猜测 ∠1 与 ∠2 的关系，并说明理由．
（2）如果 ∠ABC 是钝角，如图②，（1）中的结论是否还成立?请说明理由．

10. 如图，在折纸活动中，小明制作了一张三角形纸片 ABC，点 D，E 分别在边 AB，AC 上，将 △ABC 沿 DE 折叠压平，使点 A 与点 Aʹ 重合．
（1）若 ∠A=75∘，则 ∠1+∠2= ；
（2）若 ∠A=α，求 ∠1+∠2 的度数．

11. “8 字”的性质及应用；
（1）如图 ①，AD，BC 相交于点 O，得到一个“8 字”ABCD．求证：∠A+∠B=∠C+∠D．
（2）图 ② 中共有多少个“8 字”?
（3）如图 ②，∠ABC 和 ∠ADC 的平分线相交于点 E，利用（1）中的结论证明 ∠E=12∠A+∠C．

12. 如图，在 △ABC 中，∠ABC，∠ACB 的平分线相交于点 F．
（1）若 ∠ABC=40∘，∠ACB=50∘，求 ∠BFC 的度数；
（2）若 ∠A=70∘，求 ∠BFC 的度数；
（3）若 ∠BFC=120∘，求 ∠A 的度数；
（4）根据上述信息，试探究 ∠A 与 ∠BFC 之间的数量关系，并说明理由．
答案
1. C
2. D
3. C
4. C
5. 25∘
6. 68∘
7. 180∘
8. 36∘
9. （1） ∠1=∠2．
理由：∵ AD⊥BC，CE⊥AB，
∴ △ABD 和 △BCE 是直角三角形．
∴ ∠1+∠B=90∘，∠2+∠B=90∘．
∴ ∠1=∠2．
（2） 结论还成立．
理由：∵ AD⊥BC，CE⊥AB，
∴ ∠D=∠E=90∘．
∴ ∠1+∠CBE=90∘，∠2+∠DBA=90∘．
∵ ∠DBA=∠CBE，
∴ ∠1=∠2．
10. （1） 150∘
（2） 由折叠的性质，可知 ∠AED=∠AʹED，∠ADE=∠AʹDE，
∴ 2∠AED+∠1=180∘，2∠ADE+∠2=180∘．
∴ 2∠AED+∠ADE+∠1+∠2=360∘．
又 ∵ ∠A+∠AED+∠ADE=180∘，
∴ 2180∘-∠A+∠1+∠2=360∘．
∴ ∠1+∠2=2∠A=2α．
11. （1） 在 △OAB 中，∠A+∠B=180∘-∠AOB；
在 △OCD 中，∠C+∠D=180∘-∠COD．
∵∠AOB=∠COD，
∴∠A+∠B=∠C+∠D；
（2） 图 ② 中共有 6 个“8 字”；
（3） 在“8 字”ABED 中，∠E+∠ADE=∠A+∠ABE； ⋯⋯①
在“8 字”EBCD 中，∠E+∠EBC=∠C+∠EDC． ⋯⋯②
由 ①+②，得 2∠E+∠ADE+∠EBC=∠A+∠C+∠ABE+∠EDC．
∵ED 平分 ∠ADC，EB 平分 ∠ABC，
∴∠ADE=∠EDC，∠EBC=∠ABE．
∴2∠E=∠A+∠C，
即 ∠E=12∠A+∠C．
12. （1） ∵BD 平分 ∠ABC，
∴∠FBC=12∠ABC=20∘，
∵CE 平分 ∠ACB，
∴∠FCB=12∠ACB=25∘，
∴∠BFC=180∘-∠FBC-∠FCB=135∘．
（2） 由（1），得
∠BFC=180∘-∠FBC+∠FCB=180∘-12∠ABC+∠ACB=180∘-12180∘-∠A=90∘+12∠A=90∘+12×70∘=125∘.
（3） 由（2），得 ∠BFC=90∘+12∠A，
∴120∘=90∘+12∠A，
∴∠A=60∘．
（4） ∠BFC=90∘+12∠A．
理由：
∠BFC=180∘-∠FBC+∠FCB=180∘-12∠ABC+∠ACB=180∘-12180∘-∠A=90∘+12∠A.