数学九年级上册第2章 对称图形——圆综合与测试单元测试同步练习题

这是一份数学九年级上册第2章 对称图形——圆综合与测试单元测试同步练习题，共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
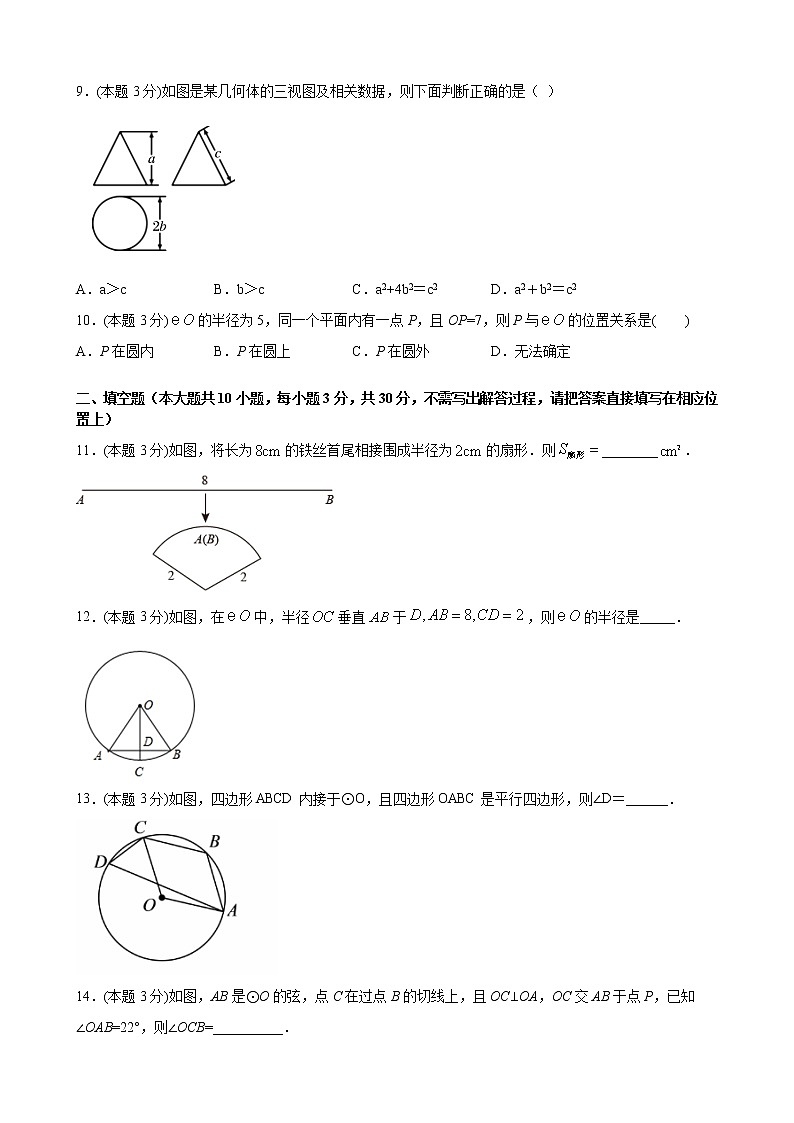
苏科九年级上   单元测试第2单元  班级________  姓名________ 一、选择题（本大题共10小题，每小题3分，共30分，在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填在相应位置上）1．(本题3分)如图，AB为⊙O的直径，点C在⊙O上，若，，则的长为（     ）A． B． C． D．2．(本题3分)在一个圆中任意画4条半径，则这个圆中有扇形（    ）A．4个 B．8个 C．12个 D．16个3．(本题3分)如图，半径为5的⊙A中，弦所对的圆心角分别是，．已知，，则弦的弦心距等于（    ）A． B． C．4 D．34．(本题3分)如图所示，是的直径，切于点，线段交于点，连接，若，则等于（    ）A． B． C． D．5．(本题3分)如图，半圆的圆心为0，直径AB的长为12，C为半圆上一点，∠CAB＝30°，的长是（   ）A．12π B．6π C．5π D．4π6．(本题3分)如图，一块直角三角板ABC的斜边AB与量角器的直径重合，点D对应54°，则∠BCD的度数为（　　）A．54° B．27° C．63° D．36°7．(本题3分)如图，半径为3的⊙O内有一点A，OA＝，点P在⊙O上，当∠OPA最大时，S△OPA等于（　　）A． B． C． D．18．(本题3分)如图，点A、B、C在上， ，垂足分别为D、E，若，则的度数为（    ）A． B． C． D．9．(本题3分)如图是某几何体的三视图及相关数据，则下面判断正确的是（ ）A．a＞c B．b＞c C．a2+4b2＝c2 D．a2＋b2＝c210．(本题3分)的半径为5，同一个平面内有一点P，且OP=7，则P与的位置关系是(     )A．P在圆内 B．P在圆上 C．P在圆外 D．无法确定 二、填空题（本大题共10小题，每小题3分，共30分，不需写出解答过程，请把答案直接填写在相应位置上）11．(本题3分)如图，将长为的铁丝首尾相接围成半径为的扇形．则________．12．(本题3分)如图，在中，半径垂直于，则的半径是_____．13．(本题3分)如图，四边形ABCD内接于⊙O，且四边形OABC是平行四边形，则∠D＝______．14．(本题3分)如图，AB是⊙O的弦，点C在过点B的切线上，且OC⊥OA，OC交AB于点P，已知∠OAB=22°，则∠OCB=__________．15．(本题3分)已知圆心角为的扇形的面积为，则扇形的弧长是________．16．(本题3分)如图，在矩形ABCD中，AB=4，AD=3，以顶点D为圆心作半径为r的圆，若要求另外三个顶点A，B，C中至少有一个点在圆内，且至少有一个点在圆外，则r的取值范围是__________．17．(本题3分)在一个圆中，有个圆心角为160°的扇形，则这个扇形的面积是整个圆面积的________.18．(本题3分)如图，△ABC内接于⊙O，若∠OBC=25°，则∠A=_____．19．(本题3分)如图，中，，，．点在边上，点是边上一点（不与点、重合），且，则的取值范围是______．20．(本题3分)如图是一个圆锥的主视图，根据图中标出的数据（单位：），计算这个圆锥侧面展开图圆心角的度数为_______．三、解答题（本大题共10小题，共60分，请在答题卷指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）21．(本题5分)如图所示是一个纸杯，它的母线延长后形成的立体图形是圆锥，该圆锥的侧面展开图是扇形OAB，经测量，纸杯开口圆的直径为6cm，下底面直径为4，母线长EF=9cm，求扇形OAB的圆心角及这个纸杯的表面积．（结果保留根号和π）    22．(本题5分)如图，大正方形的边长为8厘米，求阴影部分的周长和面积（结果保留）  23．(本题5分)如图所示，∠B＝∠OAF＝90°，BO＝3 cm，AB＝4 cm，AF＝12 cm，求图中半圆的面积．   24．(本题5分)某地出土一个明代残破圆形瓷盘，为复制该瓷盘需确定其圆心和半径，请在图中用直尺和圆规画出瓷盘的圆心（不要求写作法、证明和讨论，但要保留作图痕迹） 25．(本题5分)如图，两正方形彼此相邻且内接于半圆，若小正方形的面积为，求半圆的半径.  26．(本题5分)如图，某工厂要选一块矩形铁皮加工成一个底面半径为20 cm，高为cm的圆锥形漏斗，要求只能有一条接缝(接缝忽略不计)，请问：选长、宽分别为多少厘米的矩形铁皮，才能使所用材料最省？    27．(本题6分)已知：如图，在中，，以为直径的分别交，于点，，连结，交于点．（1）求证：．（2）若，，求的长．    28．(本题6分)如图，的两条弦（AB不是直径），点E为AB中点，连接EC，ED．（1）直线EO与AB垂直吗？请说明理由；（2）求证：．  29．(本题8分)如图，在Rt△ABC中，，AD平分∠BAC，交BC于点D，点O在AB上，⊙O经过A、D两点，交AC于点E，交AB于点F．（1）求证：BC是⊙O的切线；（2）若⊙O的半径是2cm，E是弧AD的中点，求阴影部分的面积（结果保留π和根号）  30．(本题10分)如图，在Rt△ABC中，∠C=90°，以BC为直径的⊙O交斜边AB于点M，若H是AC的中点，连接MH．（1）求证：MH为⊙O的切线．（2）若MH=，=，求⊙O的半径．（3）在（2）的条件下分别过点A、B作⊙O的切线，两切线交于点D，AD与⊙O相切于N点，过N点作NQ⊥BC，垂足为E，且交⊙O于Q点，求线段NQ的长度．
参考答案1．B2．C3．D4．A5．D6．C7．B8．C9．D10．C11．412．513．60°14．44°15．16．.17．18．65°．19．20．21．解：由题意可知：=6πcm， =4π，设∠AOB=n，AO=R，则CO=R﹣9，  由弧长公式得：l=，∴，解得：n=40，R=27，故扇形OAB的圆心角是40度．∵R=27，R﹣9=18，∴S扇形OCD= ×4π×18=36π（cm2），S扇形OAB= ×6π×27=81π（cm2），纸杯侧面积=S扇形OAB﹣S扇形OCD=81π﹣36π=45π（cm2），纸杯底面积=π•22=4π（cm2）纸杯表面积=45π+4π=49π（cm2）．22．解：周长：π×8××2+8××4=8π×+16=4π+16（厘米）；面积：8×8×+π××=32+8π（平方厘米）．答：阴影部分的周长是4π+16厘米，面积是32+8π平方厘米．23．解：如图，∵在直角△ABO中，∠B＝90°，BO＝3 cm，AB＝4 cm，∴AO＝＝5 cm.则在直角△AFO中，由勾股定理，得到FO＝＝13 cm，∴图中半圆的面积＝π×2＝π×(cm2)．答：图中半圆的面积是cm2.24．在圆上取两个弦，根据垂径定理，垂直平分弦的直线一定过圆心，所以作出两弦的垂直平分线即可．25．如下图所示，圆心为，设大正方形的边长为，圆的半径为，∵正方形有两个顶点在半圆上，另外两个顶点在圆心两侧，∴，，∵小正方形的面积为，∴小正方形的边长，由勾股定理得，，即，解得，∴.26．∵圆锥形漏斗的底面半径为20cm，高为cm，∴圆锥的母线长为R60(cm)．设圆锥的侧面展开图的圆心角为n°，则有=2π×20，解得：n=120．方案一：如图①，扇形的半径为60 cm，矩形的宽为60 cm，易求得矩形的长为 cm．此时矩形的面积为= (cm2)．方案二：如图②，扇形与矩形的两边相切，有一边重合，易求得矩形的宽为60 cm，长为30＋60=90(cm)，此时矩形的面积为90×60=5 400(cm2)．∵>5400，∴方案二所用材料最省，即选长为90 cm，宽为60 cm的矩形铁皮，才能使所用材料最省．27．（1）证明：∵AB为⊙O的直径，∴∠AEB=90°，∵AB=AC，∴∠C=∠ABC．∵BO=OD，∴∠ODB=∠ABC，∴∠C=∠ODB，∴OD//AC，∴OD⊥BE；（2）解：∵OD⊥BE，∴弧BD=弧DE，∴DB=DE=，∵AB=5，则OB=OD=，设OF=x，则DF=-x，∵BF2=BD2-DF2=OB2-OF2，即()2-(-x)2=()2-x2，解得x=，∵OF//AE，OA=OB，∴AE=2OF=2×=3．28．解：（1）直线EO与AB垂直．理由如下：如图，连接EO，并延长交CD于F．∵ EO过点O，E为AB的中点，．（2），，．∵ EF过点O，，垂直平分CD， ．29．（1）连接OD．∵OA=OD，∴∠OAD=∠ODA．∵∠OAD=∠DAC，∴∠ODA=∠DAC，∴OD∥AC，∴∠ODB=∠C=90°，∴OD⊥BC，∴BC是⊙O的切线．（2）连接OE，OE交AD于K．∵，∴OE⊥AD．∵∠OAK=∠EAK，AK=AK，∠AKO=∠AKE=90°，∴△AKO≌△AKE，∴AO=AE=OE，∴△AOE是等边三角形，∴∠AOE=60°，∴S阴=S扇形OAE﹣S△AOE22．30．解：（1）连接OH、OM，∵H是AC的中点，O是BC的中点∴OH是△ABC的中位线 ，∴OH∥AB，∴∠COH=∠ABC，∠MOH=∠OMB又∵OB=OM，∴∠OMB=∠MBO ，∴∠COH=∠MOH，在△COH与△MOH中，∵OC=OM，∠COH=∠MOH，OH=OH∴△COH≌△MOH（SAS），∴∠HCO=∠HMO=90°，∴MH是⊙O的切线；（2）∵MH、AC是⊙O的切线，∴HC=MH=，∴AC=2HC=3，∵=，∴BC=4 ，∴⊙O的半径为2；（3）连接OA、CN、ON，OA与CN相交于点I，∵AC与AN都是⊙O的切线 ，∴AC=AN，AO平分∠CAD ，∴AO⊥CN，∵AC=3，OC=2 ，∴由勾股定理可求得：AO=，∵AC•OC=AO•CI，∴CI= ，∴由垂径定理可求得：CN=，设OE=x，由勾股定理可得：，∴，∴x=，∴CE=，由勾股定理可求得：EN=，∴由垂径定理可知：NQ=2EN=．