高中数学人教版（中职）基础模块上册第五章 三角函数5.3 三角函数的图象和性质精品教学设计及反思

这是一份高中数学人教版（中职）基础模块上册第五章 三角函数5.3 三角函数的图象和性质精品教学设计及反思，共7页。教案主要包含了教学目标，教学重点，教学难点，教学设计，教学备品，课时安排，教学过程等内容，欢迎下载使用。
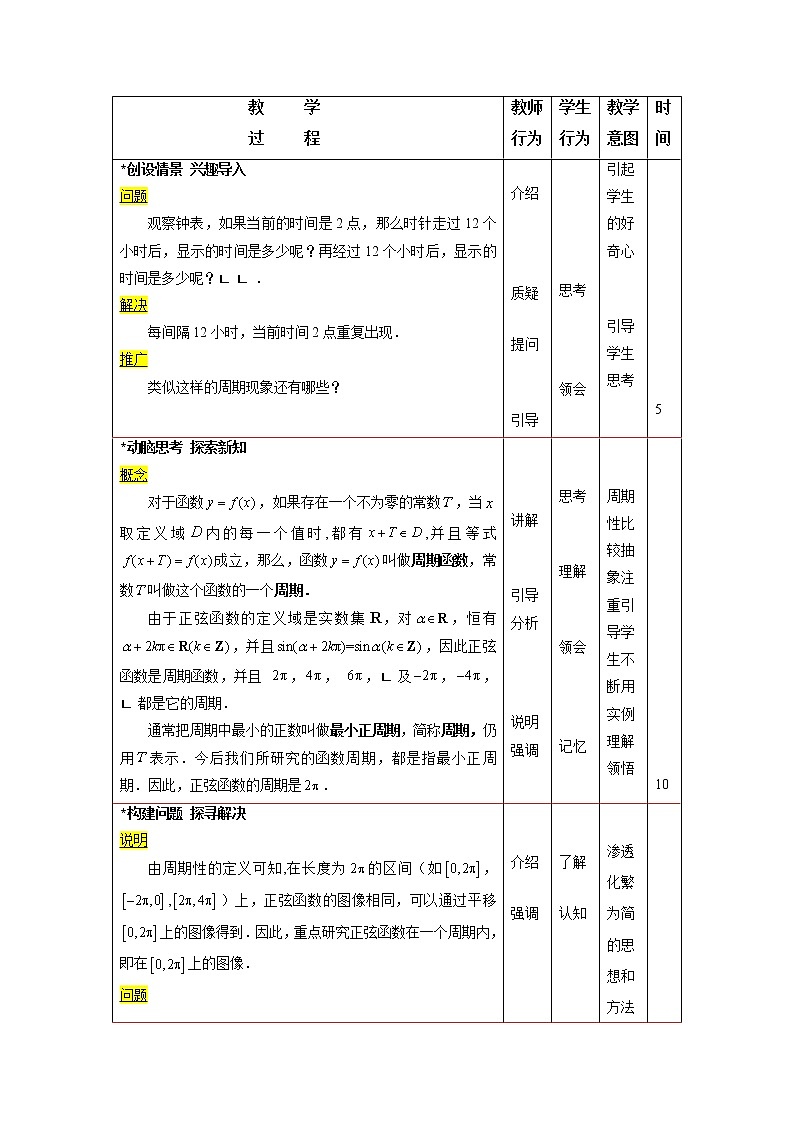
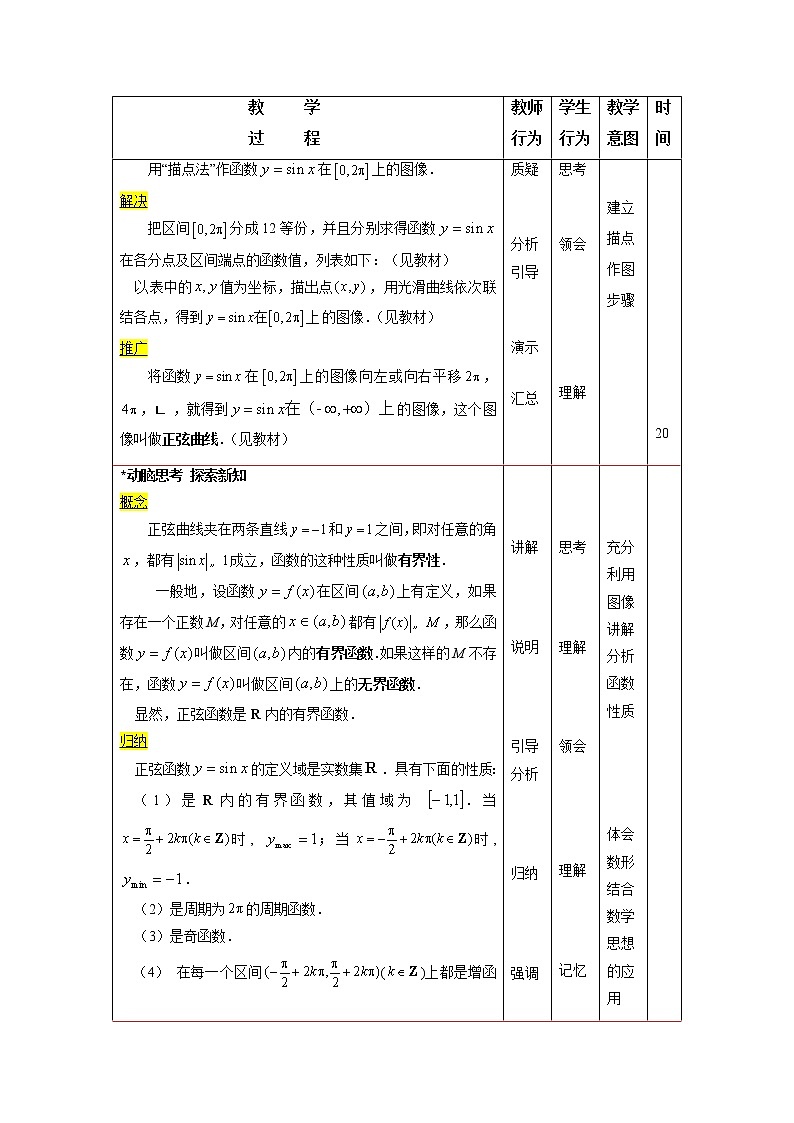
 三角函数的图像和性质 【教学目标】知识目标：(1) 理解正弦函数的图像和性质；(2) 理解用“五点法”画正弦函数的简图的方法；(3) 了解余弦函数的图像和性质．能力目标：(1) 认识周期现象，以正弦函数、余弦函数为载体，理解周期函数；(2) 会用“五点法”作出正弦函数、余弦函数的简图；(3) 通过对照学习研究，使学生体验类比的方法，从而培养数学思维能力．【教学重点】（1）正弦函数的图像及性质；（2）用“五点法”作出函数y=sinx在上的简图．【教学难点】周期性的理解．【教学设计】（1）结合生活实例，认识周期现象，介绍周期函数；（2）利用诱导公式，认识正弦函数的周期；（3）利用“描点法”及“周期性”作出正弦函数图像； （4）观察图像认识有界函数，认识正弦函数的性质；（5）观察类比得到余弦函数的性质．【教学备品】课件，实物投影仪，三角板，常规教具．【课时安排】2课时．(90分钟)【教学过程】教     学 过     程教师行为学生行为教学意图时间*揭示课题 5.6三角函数的图像和性质*创设情景 兴趣导入问题  观察钟表，如果当前的时间是2点，那么时针走过12个小时后，显示的时间是多少呢？再经过12个小时后，显示的时间是多少呢？．解决 每间隔12小时，当前时间2点重复出现．推广类似这样的周期现象还有哪些？ 介绍 介绍   质疑 提问  引导 了解     思考   领会 利用问题引起学生的好奇心  引导学生思考            5*动脑思考 探索新知概念 对于函数，如果存在一个不为零的常数，当取定义域内的每一个值时,都有,并且等式成立，那么，函数叫做周期函数，常数叫做这个函数的一个周期．由于正弦函数的定义域是实数集R，对，恒有，并且，因此正弦函数是周期函数，并且 ，， ，及，，都是它的周期．通常把周期中最小的正数叫做最小正周期，简称周期，仍用表示．今后我们所研究的函数周期，都是指最小正周期．因此，正弦函数的周期是．   讲解  引导分析   说明强调  思考  理解  领会   记忆  周期性比较抽象注重引导学生不断用实例理解领悟              10*构建问题 探寻解决说明由周期性的定义可知,在长度为的区间（如，,）上，正弦函数的图像相同，可以通过平移上的图像得到．因此，重点研究正弦函数在一个周期内，即在上的图像．问题用“描点法”作函数在上的图像．解决把区间分成12等份，并且分别求得函数在各分点及区间端点的函数值，列表如下：（见教材）以表中的值为坐标，描出点，用光滑曲线依次联结各点，得到的图像．（见教材）推广将函数在上的图像向左或向右平移，，，就得到的图像，这个图像叫做正弦曲线．（见教材）  介绍 强调   质疑  分析引导  演示 汇总    了解 认知   思考  领会     理解 渗透化繁为简的思想和方法 建立描点作图步骤                     20*动脑思考 探索新知概念正弦曲线夹在两条直线和之间，即对任意的角，都有成立，函数的这种性质叫做有界性． 一般地，设函数在区间上有定义，如果存在一个正数M，对任意的都有，那么函数叫做区间内的有界函数．如果这样的M不存在，函数叫做区间上的无界函数．显然，正弦函数是R内的有界函数．归纳正弦函数的定义域是实数集．具有下面的性质：（1）是R内的有界函数，其值域为 ．当时, ；当时,．（2）是周期为的周期函数．（3）是奇函数．（4） 在每一个区间()上都是增函数,其函数值由−1增大到1；在每一个区间()上都是减函数，其函数值由1减小到−1．   讲解   说明   引导分析   归纳   强调      思考   理解   领会    理解   记忆   充分利用图像讲解分析函数性质     体会数形结合数学思想的应用                         30*动脑思考 探索新知观察发现，正弦函数在上的图像中有五个关键点：,   ,   ,   ,   ．描出这五个点后，正弦函数,的图像的形状就基本上确定了．因此，在精确度要求不高时，经常首先描出这关键的五个点，然后用光滑的曲线把它们联结起来，从而得到正弦函数在上的简图．这种作图方法叫做“五点法”．  质疑 引领 总结   观察 思考 体会  五点可以教给学生自我发现总结        35*巩固知识 典型例题例1 利用“五点法”作函数在上的图像．分析 图像中的五个关键点的横坐标分别是0，，，，，这里要求出在五个相应的函数值，从而得到五个点的坐标，最后用光滑的曲线联结这五个点，得到图像．解  列表0010−1012101 以表5-6中每组对应的x,y值为坐标，描出点，用光滑的曲线顺次联结各点,得到函数在上的图像． 例2  已知, 求的取值范围．解  因为≤，所以≤，即  ，解得         ． 故的取值范围是．例3  求使函数取得最大值的的集合，并指出最大值是多少．分析 将看作正弦函数中的自变量，因此需要进行变量替换．解  设，则使函数取得最大值1的集合是，由          ,   得            ．故所求集合为 ，函数的最大值是．    说明  讲解     引领   质疑 分析  归纳  强调 启发  引导   讲解   观察   思考 主动求解    理解   讨论 求解  思考  领会   明确   理解  安排与知识点对应例题巩固新知 注重画图时对细节的强调和引领 不等式的求解过程可以教给学生独立完成 引导学生体会换元数学方法思想                                     50*运用知识 强化练习   教材练习1．利用“五点法”作函数在上的图像．2．利用“五点法”作函数在上的图像．3．已知 ， 求的取值范围．4．求使函数取得最大值的的集合，并指出最大值是多少?  提问 巡视 指导  动手求解 交流  关注学生知识掌握情况       55*构建问题 探寻解决 余弦函数的定义域是．由于对恒有并且，可知余弦函数是周期函数，其周期是．问题 用“描点法”作出余弦函数在上的图像．解决把区间分成12等份，并且分别求得函数在各分点及区间端点的函数值，列表（见教材）．以表中的值为坐标，描出点，用光滑曲线顺次联结各点，得到函数的图像（见教材）． 推广将函数的图像向左或向右平移，，，,就得到余弦函数的图像（见教材）．这个图像叫做余弦曲线．  介绍 强调 质疑 分析  引导 演示 总结  了解 认知 思考  领会  主动求解 理解渗透化繁为简的思想和方法  注意图像细节处理                 65*动脑思考 探索新知归纳余弦函数的定义域是实数集R，余弦函数有如下性质： ⑴ 是有界函数，其值域为．当时, ；当时, ． ⑵ 是周期为的函数． ⑶ 是偶函数．⑷ 在区间内是增函数，函数值从增加到；在区间内是减函数，函数值从减少到．  讲解  引导分析 归纳  强调   思考  理解 领会   记忆充分利用图像讲解分析函数性质  类比正弦函数            70*巩固知识 典型例题例4  用“五点法”作出函数在上的图像．分析 图像中的五个关键点的横坐标分别是0，，，，，这里要求出在这五个关键点上的相应函数值，从而得到五个点的坐标，最后用光滑的曲线联结这五个点，得到图像．解  列表10−101−1010−1 以表中的值为坐标，描出点，然后用光滑的曲线顺次联结各点，得到函数的图像   质疑  说明    引领讲解  汇总总结  观察  思考    主动求解  理解领悟  强调五点的特点  注意作图的步骤和方法                    75*运用知识 强化练习   教材练习用“五点作图法”作出函数在 上的图像．  提问巡视指导 动手求解交流 纠错答疑   80*归纳小结 强化思想本次课学了哪些内容？重点和难点各是什么？ *自我反思 目标检测 本次课采用了怎样的学习方法？你是如何进行学习的？你的学习效果如何？ 引导  提问  回忆  反思交流培养学生总结反思学习过程能力       85