初中数学人教版七年级上册4.2 直线、射线、线段说课课件ppt

这是一份初中数学人教版七年级上册4.2 直线、射线、线段说课课件ppt，共20页。PPT课件主要包含了比较线段的长短，线段的和与差，ACa+b，ADa-b，直线n等内容，欢迎下载使用。
1.会用尺规作图法画一条线段等于已知线段，会比较两条线段的长短.2.理解线段等分点的意义，理解两点间距离的意义，了解“两点之间，线段最短”的线段性质.
如何比较线段AB与线段CD的长短？
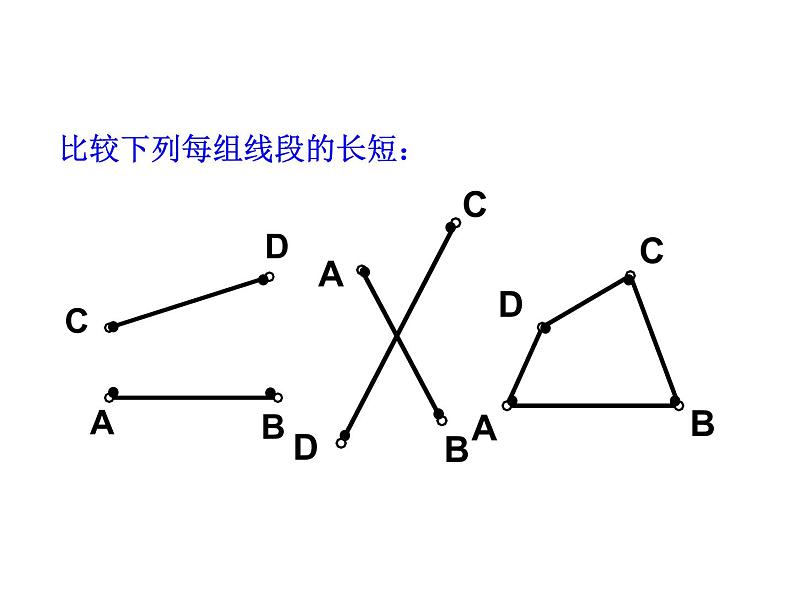
比较下列每组线段的长短：
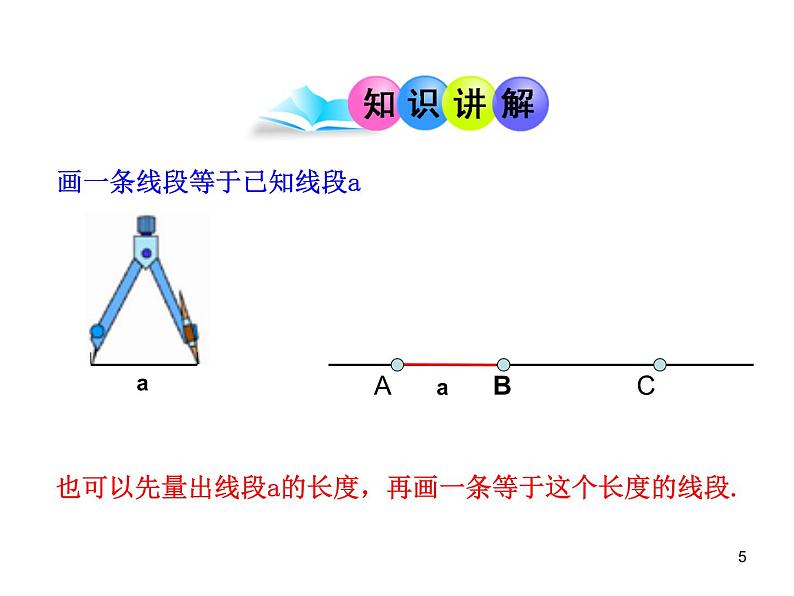
画一条线段等于已知线段a
也可以先量出线段a的长度，再画一条等于这个长度的线段.
A B
A B C D
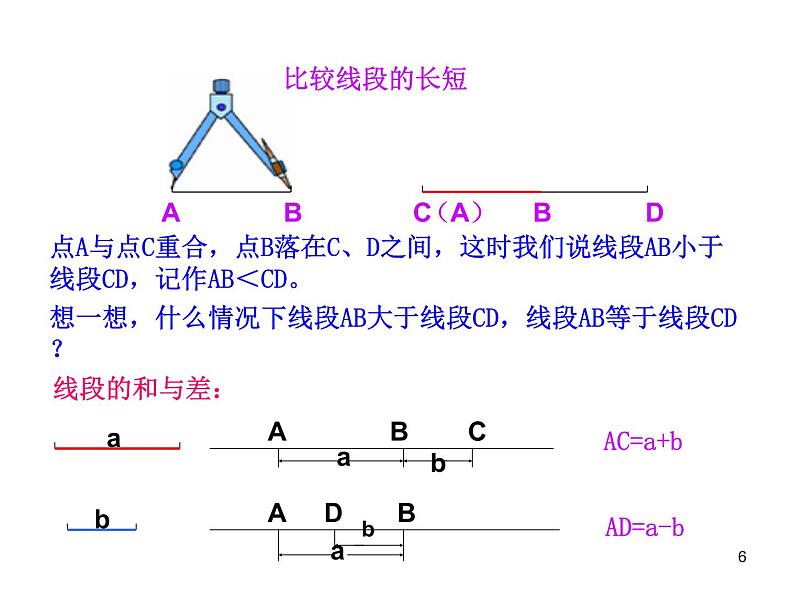
点A与点C重合，点B落在C、D之间，这时我们说线段AB小于线段CD，记作AB＜CD。
想一想，什么情况下线段AB大于线段CD，线段AB等于线段CD？
A B
A B
M N
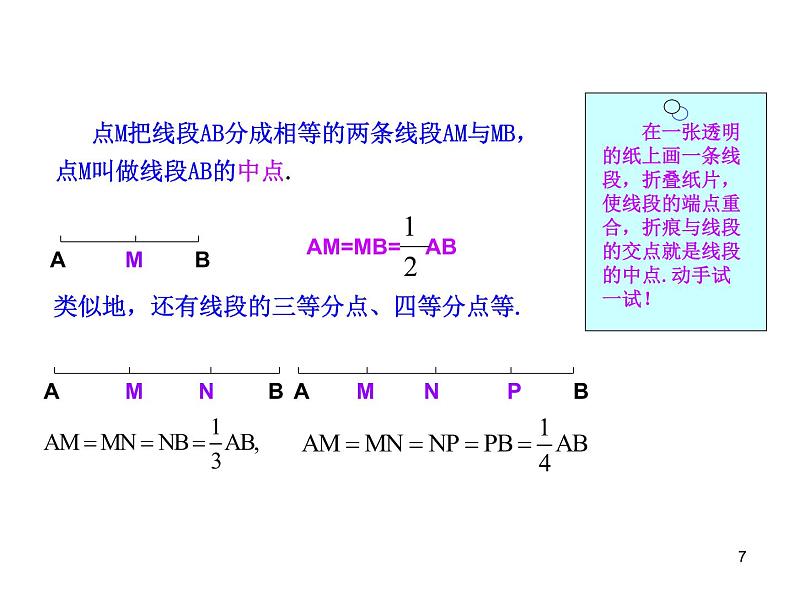
在一张透明的纸上画一条线段，折叠纸片，使线段的端点重合，折痕与线段的交点就是线段的中点.动手试一试！
点M把线段AB分成相等的两条线段AM与MB，点M叫做线段AB的中点.
A B
类似地，还有线段的三等分点、四等分点等.
A B
M N P
如图所示，已知线段a，b.画一条线段，使它等于2a-b.
解：令AB=BC=2a,CD=b,如下图所示：
A B
所以线段AD就是所求的线段.
如图,已知线段AB,延长线段AB到C,使BC=AB.
在所画图中,我们把点B叫做线段AC的中点
如果点B为线段AC的中点,那么AC= AB= BC;AB= = AC.
1.如图所示，点C是线段AB的中点,（1）若AB=6cm，则AC= cm.（2）若AC=6cm，则AB= cm.
2.已知：AD=4cm,BD=2cm,C为AB的中点，则BC=_____cm.
3.在同一条直线上依次有A,B,C三点，取AB的中点M,取BC的中点N,如果AC=6cm,则MN=______cm.
4.点C是AB延长线上的一点,点D是AB中点,如果点B恰好是DC的中点,设AB=2cm，则 AC=______cm.
5.点A,B,C,D是直线上顺次四个点，且AB:BC:CD=2:3:4,如果AC=10cm,那么BC=_______cm.
如图所示，要从甲地到乙地去，有３条路线，请你选择一条相对近一些的路线.
从甲地到乙地能否修一条最近的路？如果能，你认为这条路应该怎样修？
生活常识告诉我们： 结论：两点之间的所有连线中，线段最短.
定义：两点之间线段的长度叫做两点之间的距离.
如图所示,线段AB=8cm，点C是AB的中点，点D在CB上且DB=1.5cm，求线段CD的长度.
解：CB= AB=4cm， CD=CB-DB =4cm-1.5cm=2.5cm.
1.判断题：(1)一条直线长100米. （ ）(2)手电筒照在墙上，从灯泡到墙上的光线是射线. （ ）(3)线段是直线的一部分. （ ）(4)直线比射线长. （ ）(5)在射线上可以截取2厘米长的线段. （ ） (6)过一个点只可以画一条射线. ( ）
2.某班的同学在操场上站成笔直的一排，确定两个同学的位置,这一排的位置就确定下来了，这是因为________________________________.
经过两点有且只有一条直线
3.分别用两种方式表示图中的直线.
直线 AO、直线 BO
4.如图所示,线段AB=8cm，点C是AB的中点，点D是AC的中点，点E是CB的中点，求线段DE的长度.
解：AC=BC= AB=4cm， DC= AC=2cm,EC= CB=2cm,DE=DC+CE=2cm+2cm=4cm.
5.如图所示,点B,C在线段AD上.（1）图中以A为端点的线段有哪些？以B为端点的线段有哪些？
解:以A为端点的线段有:线段AB,线段AC,线段AD.以B为端点的线段有:线段BA,线段BC,线段BD.
（2）图中共有多少条线段？请分别说出这些线段.
解:图中共有6条线段,分别是线段AB,线段AC,线段AD,线段BC,线段BD,线段CD.