人教B版 (2019)必修 第一册3.1.1 函数及其表示方法精品ppt课件

课题名

3.1.1 函数及其表示方法（第2课时）

课标要求

1.会选择恰当的方法表示函数,并注意体会三种表示方法的区别与联系.(数学抽象)

2.掌握求函数解析式的一般方法.(数学运算)

3.了解简单的分段函数,并能简单应用.(逻辑推理)

核心目标

1.选择恰当的方法表示函数,并注意体会三种表示

方法的区别与联系.(数学抽象)

2.掌握求函数解析式的一般方法.(数学运算)

3.了解简单的分段函数,并能简单应用.(逻辑推理)

教学准备

教师准备：教案、课件

学生准备：教材、学案

教学过程

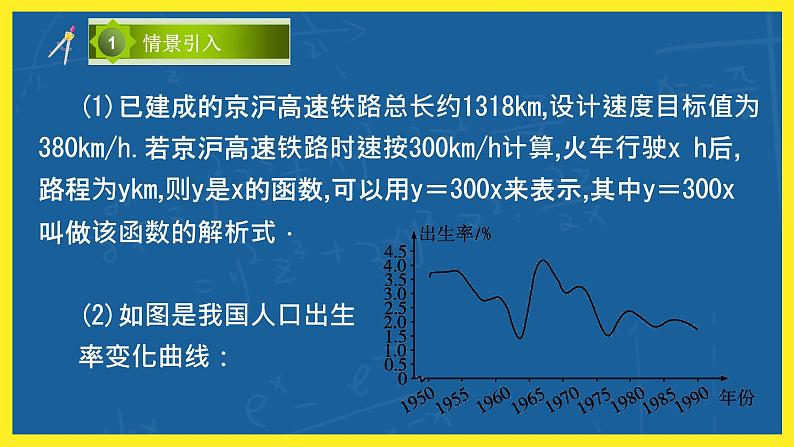
情景引入

(1)已建成的京沪高速铁路总长约1318km,设计速度目标值为380km/h.若京沪高速铁路时速按300km/h计算,火车行驶x h后,路程为ykm,则y是x的函数,可以用y＝300x来表示,其中y＝300x叫做该函数的解析式．

(2)如图是我国人口出生率变化曲线：

(3)下表是大气中氰化物浓度与污染源距离的关系表：

[问题]　根据初中所学知识，说出上述分别是用什么法表示函数的？

新知探究

知识点一　函数的表示方法

知识点二   分段函数

     如果一个函数，在其定义域内，对于自变量的不同取值区间，有不同的对应方式，则称其为分段函数．

名师点析 学习分段函数应注意

(1)分段函数是一个函数,而不是几个函数.

(2)处理分段函数问题,要先确定自变量取值属于哪个范围,再选取相应的对应关系.注意写解析式时各区间端点的开闭,做到不重复、不遗漏.

(3)分段函数的定义域是各段定义域的并集,值域是分别求出各段上的值域后取并集.

核心目标检验

1.购买某种饮料x听，所需钱数为y元，若每听2元，用解析法将y表示成x(x∈{1，2，3，4})的函数为(　　)

A．y＝2x　　　　　　　　　   B．y＝2x(x∈R)

C．y＝2x(x∈{1，2，3，…})    D．y＝2x(x∈{1，2，3，4})

解析：题中已给出自变量的取值范围，x∈{1，2，3，4}.

2．已知函数f(x)＝，则f(2)等于(　　)

 A．0      B．1/3     C．1       D．2

解析：f(2)＝√2−1＝1.

3．已知函数f(2x＋1)＝6x＋5，则f(x)的解析式是(　　)

  A．3x＋2    B．3x＋1

  C．3x－1    D．3x＋4

解析：方法一　令2x＋1＝t，则x＝t−1/2.

∴f(t)＝6×t−1/2＋5＝3t＋2.∴f(x)＝3x＋2.

方法二　∵f(2x＋1)＝3(2x＋1)＋2.∴f(x)＝3x＋2.

4．已知函数f(x)，g(x)分别由下表给出．

解析：由于函数关系是用表格形式给出的，知g(1)＝3，

∴f(g(1))＝f(3)＝1.由于g(2)＝2，∴f(x)＝2，∴x＝1.

课堂总结

1.选择恰当的方法表示函数,并注意体会三种表示

方法的区别与联系.

2.掌握求函数解析式的一般方法.

3.了解简单的分段函数,并能简单应用.

命题讲练

命题方向1：函数的表示方法

例题1:某学生离家去学校，一开始跑步前进，跑累了再走余下的路程．下列图中纵轴表示离校的距离，横轴表示出发后的时间，则较符合该学生走法的是(　　)

【解析】　(1)由题意可知，一开始速度较快，后来速度变慢，所以开始曲线比较陡峭，后来曲线比较平缓，又纵轴表示离校的距离，所以开始时距离最大，最后距离为0.

跟踪练习1:已知函数f(x)按下表给出，满足f(f(x))＞f(3)的x的值为________．

分析：观察表格，先求出f(1)、f(2)、f(3)，进而求出f(f(x))的值，再与f(3)比较．

【解析】(2)由表格可知f(3)＝1，故f(f(x))>f(3)即为f(f(x))>1.

∴f(x)＝1或f(x)＝2，∴x＝3或1.

命题方向2:函数图像的作法及应用

例题2:作出下列函数的图像并求出其值域：

(1)  y＝2x＋1，x∈[0，2]；

(2)  y＝2/x，x∈[2，＋∞)；

(3)y＝＋2x，x∈[－2，2]．

[解]　(1)当x∈[0，2]时，图像是直线y＝2x＋1的一部分图(如图①)，观察图像可知，其值域为[1，5]．

[解](2)当x∈[2，＋∞)时，图像是反比例函数y＝2/x的一部分(如图②)，观察图像可知其值域为(0，1]．

(3)当－2≤x≤2时，图像是抛物线y＝＋2x的一部分(如图③)．

由图可得函数的值域是 [－1，8]．

描点法作函数图像的步骤

(1)列表：先找出一些有代表性的自变量x的值，再计算出相对应的函数值f(x)，并用表格的形式表示出来；

(2)描点：把表格中的点(x，f(x))一一在坐标系中描出来；

(3)连线：用光滑的曲线把这些点按自变量由小到大(或由大到小)的顺序连接起来．　

[注意]　(1)画函数的图像时要注意函数的定义域；(2)要作出更精确的图像，常常需要描出更多的点．

跟踪练习2：1.已知函数f(x)的图像如图所示，则此函数的定义域是________，值域是________．

解析：结合图像，知函数f(x)的定义域为[－3，3]，值域为[－2，2]．

2．作出下列函数的图像，并根据图像求其值域：

(1)

(2)y＝－4/x，x∈[－3，0)∪(0，1]；

(3)y＝＋4x＋1，x∈[－3，0]．

解：(1)该函数的图像如图①所示，由图可知值域为{－3，1，2，3}．

(2)作出函数y＝－4/x，x∈[－3，0)∪(0，1]的图像，如图②所示，

由图像可知值域为(－∞，－4]∪[4/3,+∞).

(3)作出函数y＝＋4x＋1，x∈[－3，0]的图像，如图③所示，由图像可知值域为[－3，1]．

命题方向3:已知函数的类型，求函数的解析式

例题3:(1)已知一次函数f(x)满足f(f(x))＝4x＋6，则f(x)的解析式为                         ；

(2)已知二次函数f(x)满足f(0)＝1，f(1)＝2，f(2)＝5，则该二次函数的解析式为________．

[解析]　[解析]　(1)设f(x)＝ax＋b(a≠0)，

则f(f(x))＝f(ax＋b)＝a(ax＋b)＋b＝x＋ab＋b＝4x＋6，

于是有,解得,或,

所以f(x)＝2x＋2或f(x)＝－2x－6.

(2)设二次函数的解析式为f(x)＝a＋bx＋c(a≠0)，

      由题意得 故f(x)＝＋1.

待定系数法求函数解析式

已知函数类型求函数解析式，常采用待定系数法．步骤如下：

(1)设出含有待定系数的解析式．如一次函数的解析式设为f(x)＝ax＋b(a≠0)，反比例函数的解析式设为f(x)＝x(k)(k≠0)，二次函数的解析式设为f(x)＝ax2＋bx＋c(a≠0)；

(2)把已知条件代入解析式，列出关于待定系数的方程或方程组；

(3)解方程或方程组，得到待定系数的值；

(4)将所求待定系数的值代回所设解析式．

命题方向4:已知f(g(x))的解析式，求f(x)的解析式

例题4:(1)已知函数f(x＋1)＝＋2x，则f(x)的解析式为(　　)

  A．f(x)＝＋1　  B．f(x)＝＋2x－1

  C．f(x)＝－1   D．f(x)＝＋2x＋1

(2)已知f(√x＋1)＝x＋2√x，则f(x)的解析式为________．

解:(1)法一(换元法)：令x＋1＝t，则x＝t－1，t∈R，

        所以f(t)＝＋2(t－1)＝－1，即f(x)＝x－1.

     法二(配凑法)：因为＋2x＝(＋2x＋1)－1＝－1，

        所以f(x＋1)＝－1，即f(x)＝－1.

解:(2)法一(换元法)：令t＝√x＋1，则x＝(t−1)^2，t≥1，

         所以f(t)＝(t−1)^2＋2(t－1)＝t^2－1(t≥1)，

         所以函数的解析式为f(x)＝x^2－1(x≥1)．

     法二(配凑法)：f(√x＋1)＝x＋2√x＝x＋2√x＋1－1

                ＝(√x−1)^2－1.

   因为√x＋1≥1，所以函数的解析式为f(x)＝x^2－1(x≥1)．

换元法、配凑法求函数解析式

已知f(g(x))＝h(x)，求f(x)的两种方法

(1)换元法：即令t＝g(x)，解出x，代入h(x)中，得到一个含t的解析式，再用x替换t，便得到f(x)的解析式．

利用换元法解题时，换元后要确定新元t的取值范围，即函数f(x)的定义域；

(3)  配凑法：即从f(g(x))的解析式中配凑出“g(x)”，即用g(x)来表示h(x)，然后将解析式中的g(x)用x代替即可．

命题方向5: 已知中含有f(x)，f(1/x)或f(x)，f(－x)形式的函数，求f(x)的解析式

例题5:(1)已知函数f(x)满足f(x)＋2f(1/x)＝x，则函数f(x)的解析式为________；

(2)已知af(x)＋f(－x)＝bx，其中a≠±1，则函数f(x)的解析式为________．

解:(1)在已知等式中，将x换成1/x，得f(1/x)＋2f(x)＝1/x，

       与已知方程联立，得,

     消去f(1/x)，得f(x)＝－x/3＋2/3x.

解:(2)在原式中以－x替换x，得af(－x)＋f(x)＝－bx，

于是得,消去f(－x)，得f(x)＝bx/a−1.

故f(x)的解析式为f(x)＝b/a−1x，a≠±1.

消元法(或解方程组法)求函数解析式

在已知式子中，含有关于两个有着某种关系的不同变量的函数，这时就要依据两个变量的关系，建立一个新的关于这两个变量的式子，由两个式子建立方程组，消去一个变量，得到目标变量的解析式，这种方法称为消元法(或解方程组法)．

即已知f(x)与f(φ(x))满足的关系式，要求f(x)时，可用φ(x)代替两边的所有的x，得到关于f(x)及f(φ(x))的方程组，解之即可求出f(x)．

跟踪练习5:若3f(x－1)＋2f(1－x)＝2x，则f(x)的解析式为________．

解析：令t＝x－1，则x＝t＋1，t∈R，

原式变为3f(t)＋2f(－t)＝2(t＋1)． ①

以－t代替t，①式变为3f(－t)＋2f(t)＝2(1－t)， ②

由①②消去f(－t)得f(t)＝2t＋2/5，故f(x)＝2x＋2/5.

思想方法技巧

函数图像的三种变换

1．函数图像的平移变换

左加右减：函数y＝f(x)的图像沿x轴方向向左(a>0)或向右(a<0)平移|a|个单位长度得到函数y＝f(x＋a)的图像．上加下减：函数y＝f(x)的图像沿y轴方向向上(b>0)或向下(b<0)平移|b|个单位长度得到函数y＝f(x)＋b的图像．

例如：函数f(x)＝x2，分别作出y＝f(x＋1)，y＝f(x－1)，h＝f(x)＋1，y＝f(x)－1的图像如图所示．

向左平移一个单位

向右平移一个单位

向上平移一个单位

向下平移一个单位

2．函数图像的对称变换

(1)y＝f(x)□→┴关于x轴对称y＝－f(x)；

(2)y＝f(x)□→┴关于y轴对称y＝f(－x)；

(3)y＝f(x)□→┴关于原点对称y＝－f(－x)．

例如：f(x)＝1/x(x>0),分别作出y＝－f(x),y＝f(－x),y＝－f(－x)的图像如图所示．

3．函数图像的翻折变换

(1)y＝f(x)□→┴x轴上方图像不变,x轴下方图像翻折到x轴上方y＝|f(x)|；

(2)y＝f(x)□→┴y轴右侧图像不变,y轴右侧图像翻折到y轴左侧y＝f(|x|)．

例如：已知函数y＝f(x)＝x^2－2x－3，分别作出函数y＝|f(x)|与y＝f(|x|)的图像如图所示．

y＝|f(x)|的图像为保留y＝f(x)图像在x轴上方的部分，把x轴下方的部分沿x轴翻折上去．

y＝f(|x|)的图像为保留y＝f(x)图像在y轴右侧的部分，把y轴右侧的图像翻折到y轴左侧．

布置作业

教材练习题

教辅练习题

板书设计

一、 

二、 

教学反思