初中数学苏科版九年级上册第3章 数据的集中趋势和离散程度综合与测试单元测试课时作业

这是一份初中数学苏科版九年级上册第3章 数据的集中趋势和离散程度综合与测试单元测试课时作业，共9页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
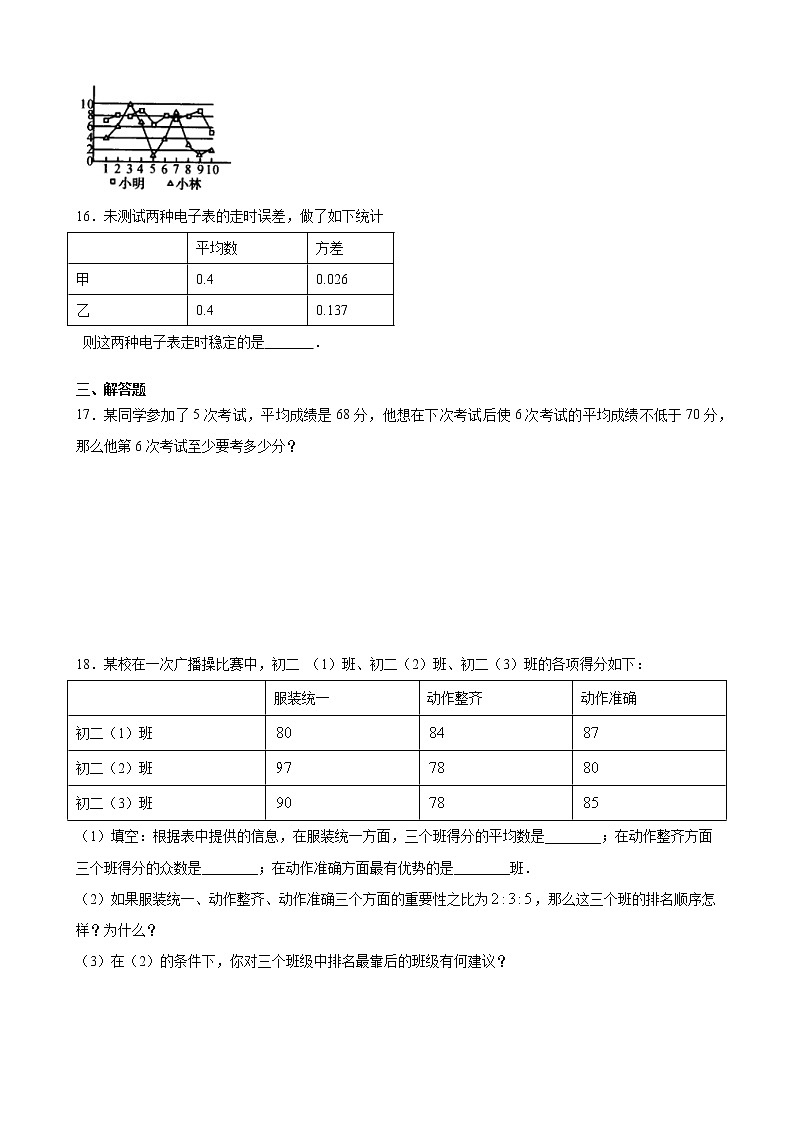
苏科九年级上   综合练习第3单元  班级________  姓名________ 一、单选题1．将一组数据中的每一个数减去50后，所得新的一组数据的平均数是2，则原来那组数据的平均数是（  ）A．50 B．52 C．48 D．22．为了调查某一路口某时段的汽车流量．记录了15天同一时段通过该路口的汽车辆数，其中有2天是142辆，2天是145辆，6天是156辆，5天是157辆．那么这15天在该时段通过该路口的汽车平均辆数为（    ）A．146辆 B．150辆 C．153辆 D．600辆3．在学校举行“阳光少年，励志青春”的演讲比赛中，五位评委给选手小明的评分分别是90，85，90，80，95，则这组数据的中位数是（    ）A．95 B．90 C．85 D．804．某公司10名职工的5月份工资统计如下，该公司10名职工5月份工资的众数和中位数分别是(    )工资（元）2000220024002600人数（人）1342A．2400元、2400元B．2400元、2300元C．2200元、2200元D．2200元、2300元5．下表是某校合唱团成员的年龄分布：年龄/岁13141516频数515对于不同的，下列关于年龄的统计量不会发生改变的是（    ）A．平均数､中位数 B．中位数､方差 C．平均数､方差 D．众数､中位数6．小广,小娇分别统计了自己近5次数学测试成绩，下列统计量中能用来比较两人成绩稳定性的是(    )A．方差 B．平均数 C．众数 D．中位数7．甲、乙、丙、丁四人进行射箭测试，每人10次射箭成绩的平均成绩都相同，方差分别是S甲2=0.65，S乙2=0.55，S丙2=0.50，S丁2=0.45，则射箭成绩最稳定的是（　　）A．甲 B．乙 C．丙 D．丁8．已知一组数据：92，94，98，91，95的中位数为a，方差为b，则a+b=（　　）A．98 B．99 C．100 D．102 二、填空题9．在一次区级数学竞赛中，某校8名参赛学生的成绩与全区参赛学生平均成绩80分的差分别为单位：分：5，，8，14，7，5，9，，则该校8名参赛学生的平均成绩是______ ．10．下表列出了某地农作物生长季节每月的降雨量（单位：）：月份四五六七八九降雨量20558213511690其中有______个月的降雨量比这6个月平均降雨量大.11．、、三个数的平均数是6，则，，的平均数是______.12．一名射击运动员连续打靶8次，命中的环数如图所示，这组数据的中位数是__________环，众数是__________环．13．为响应“书香校园”建设号召，在全校形成良好的人文阅读风尚，我县某中学随机抽取了部分学生平均每天的阅读时间，统计结果如图所示，则在本次调查中，阅读时间的中位数是_______小时，平均每人阅读时间是_______小时.14．一个样本为1、3、2、2、a，b，c．已知这个样本的众数为3，平均数为2，那么这个样本的方差为_____．15．有两名学员小林和小明练习射击，第一轮10枪打完后两人打靶的环数如图所示，通常新手的成绩不太稳定，那么根据图中的信息，估计小林和小明两人中新手是_______.16．未测试两种电子表的走时误差，做了如下统计 平均数方差甲0.40.026乙0.40.137 则这两种电子表走时稳定的是　   　． 三、解答题17．某同学参加了5次考试，平均成绩是68分，他想在下次考试后使6次考试的平均成绩不低于70分，那么他第6次考试至少要考多少分？      18．某校在一次广播操比赛中，初二 （1）班、初二（2）班、初二（3）班的各项得分如下： 服装统一动作整齐动作准确初二（1）班初二（2）班初二（3）班（1）填空：根据表中提供的信息，在服装统一方面，三个班得分的平均数是________；在动作整齐方面三个班得分的众数是________；在动作准确方面最有优势的是________班．（2）如果服装统一、动作整齐、动作准确三个方面的重要性之比为，那么这三个班的排名顺序怎样？为什么？（3）在（2）的条件下，你对三个班级中排名最靠后的班级有何建议？      19．在一次数学考试中，从某班随机抽取的10名学生得分(单位：分)如下：75，85，90，90，95，85，95，95，100，98.(1)求这10名学生得分的众数、中位数和平均数；(2)若该班共有40名学生，估计此次考试的平均成绩约为多少．      20．甲、乙两名队员参加射击训练，成绩分别被制成下列两个统计图：根据以上信息，整理分析数据如下： 平均成绩/环中位数/环众数/环方差甲a771.2乙7b8c（1）写出表格中a，b，c的值；（2）分别运用表中的四个统计量，简要分析这两名队员的射击训练成绩．若选派其中一名参赛，你认为应选哪名队员．       21．甲、乙两位同学进行投篮比赛，每人在相同时间内分别投6场，下表是甲、乙两位同学每场投中篮球个数的统计情况.对象一二三四五六甲6759510乙656799下面是甲、乙两位同学的三种说法.①乙：我的投篮成绩比甲稳定；②甲：若每一场我多投中一个球，投篮成绩就比乙稳定；③乙：若每场我投中的个数是原来的3倍，而甲每场投中的个数是原来的2倍，则我的投篮成绩的稳定程度比甲好.请判断他们说法的正确性，并说明理由.    22．某工厂甲、乙两名工人参加操作技能培训，现分别从他们在培训期间参加的若干次测试成绩中随机抽取5次，记录如下：甲8588848583乙8387848685（1）请你分别计算这两组数据的平均数；（2）现要从中选派一人参加操作技能比赛，从统计学的角度考虑，你认为选派哪名工人参加合适？请说明理由．        23．在“全民读书月”活动中，小明调查了班级里40名同学本学期计划购买课外书的花费情况，并将结果绘制成如图所示的统计图，请根据相关信息，解答下列问题：（直接填写结果）（1）本次调查获取的样本数据的众数是　   　；（2）这次调查获取的样本数据的中位数是 　；（3）若该校共有学生1000人，根据样本数据，估计本学期计划购买课外书花费50元的学生有　   　人．
参考答案1．B2．C3．B4．A5．D6．A7．D8．C9．8510．311．1412．8.5    8    13．1 ；    l.1.    14．．15．小林16．甲17．解：设第6次成绩为分，则由题意得，解得，所以他第6次考试至少要考80分.18．（1）服装统一方面的平均分为:=89分；
动作整齐方面的众数为78分；
动作准确方面最有优势的是初二（1）班；
（2）∵初二（1）班的平均分为： =84.7分；
初二（2）班的平均分为：=82.8分；
初二（3）班的平均分为： =83.9；
∴排名最好的是初二一班，最差的是初二（2）班；
（3）加强动作整齐方面的训练，才是提高成绩的基础．19．解：(1)数据由小到大排列为75，85，85，90，90，95，95，95，98，100，所以这10名学生得分的众数为95分，中位数为＝92.5(分)，平均数为 (75＋85＋85＋90＋90＋95＋95＋95＋98＋100)＝90.8(分)．(2)估计此次考试的平均成绩约为90.8分．20．（1），将乙射击的环数重新排列为：3、4、6、7、7、8、8、8、9、10，∴乙射击的中位数，∵乙射击的次数是10次，∴=4.2；（2）从平均成绩看，甲、乙的成绩相等，都是7环；从中位数看，甲射中7环以上的次数小于乙；从众数看，甲射中7环的次数最多，而乙射中8环的次数最多；从方差看，甲的成绩比乙稳定，综合以上各因素，若派一名同学参加比赛的话，可选择乙参赛，因为乙获得高分的可能性更大.21．①甲的平均成绩为（个）.甲的方差.乙的平均成绩为（个），乙的方差.因为甲、乙的平均成绩相同，且，所以乙的投篮成绩比甲稳定，所以乙的说法正确.②甲变化后的成绩为7，8，6，10，6，11，甲变化后的平均成绩为（个），甲变化后的方差为，由甲的方差不变，可知甲的说法是错误的.③甲变化后的平均成绩为（个），方差约为，乙变化后的平均成绩为（个），方差约为.因为.所以变化后乙的投篮成绩的稳定程度没有甲的好，所以乙的说法是不正确的.22．解：（1）甲平均数：×（85+88+84+85+83）＝×425＝85，乙平均数：×（83+87+84+86+85）＝×425＝85；（2）选派乙工人参加合适．理由如下：S甲2＝×[（85﹣85）2+（88﹣85）2+（84﹣85）2+（85﹣85）2+（83﹣85）2]，＝×（0+9+1+0+4），＝2.8，S乙2＝×[（83﹣85）2+（87﹣85）2+（84﹣85）2+（86﹣85）2+（85﹣85）2]，＝×（4+4+1+1+0），＝2，∵2.8＞2，∴S甲2＞S乙2，∴乙成绩更稳定，∴选派乙工人参加合适．23．（1）花费30元的有12人，最多，故众数是30元；（2）一共有40个数据，排序后第20、21个数据的平均数即是中位数，6+12=18<20，6+12+10=28>20，故第20、21个数据都是50元，故中位数是50元；（3）10÷40×2400=600（人），故估计本学期计划购买课外书花费50元的学生有50人．