江苏省泰州市海陵区五校2021-2022学年八年级下学期期中考试数学试卷(含答案)

2021～2022学年度第二学期期中考试

八年级数学试题

（考试时间:150分钟，满分150分）  成绩        

一、选择题（本大题共6小题，每小题3分，共18分）

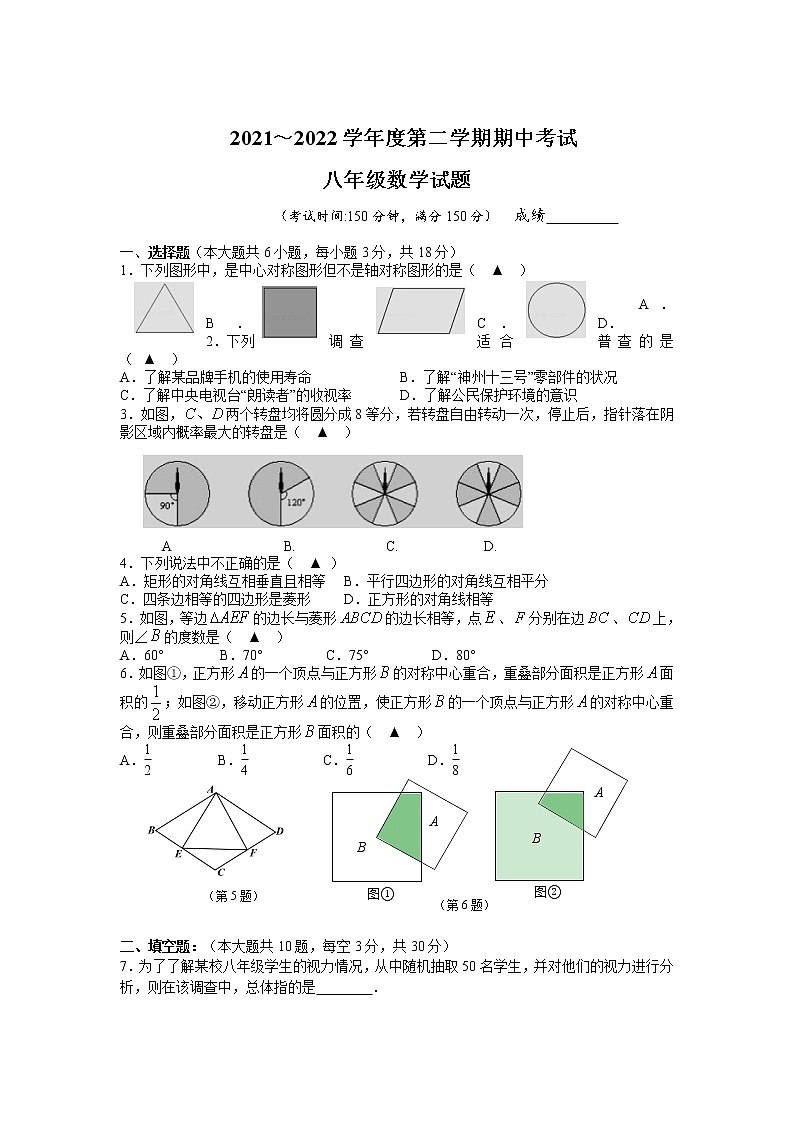
1．下列图形中，是中心对称图形但不是轴对称图形的是（  ▲  ）

A．               B．             C．                 D．   

2．下列调查适合普查的是（  ▲  ）

A．了解某品牌手机的使用寿命    B．了解“神州十三号”零部件的状况

C．了解中央电视台“朗读者”的收视率  D．了解公民保护环境的意识

3．如图，两个转盘均将圆分成8等分，若转盘自由转动一次，停止后，指针落在阴影区域内概率最大的转盘是（  ▲  ）

A                B.           C.           D.

4．下列说法中不正确的是（  ▲ ）

A．矩形的对角线互相垂直且相等 B．平行四边形的对角线互相平分 

C．四条边相等的四边形是菱形     D．正方形的对角线相等

5．如图，等边的边长与菱形的边长相等，点、分别在边、上，则∠的度数是（  ▲  ）

A．60°        B．70°         C．75°         D．80°

6．如图①，正方形的一个顶点与正方形的对称中心重合，重叠部分面积是正方形面积的；如图②，移动正方形的位置，使正方形的一个顶点与正方形的对称中心重合，则重叠部分面积是正方形面积的（  ▲  ）

A．       B．          C．         D．

二、填空题：（本大题共10题，每空3分，共30分）

7．为了了解某校八年级学生的视力情况，从中随机抽取50名学生，并对他们的视力进行分析，则在该调查中，总体指的是        ．

8．如图，矩形的对角线与相交于点，，、分别为、的中点，则的长度为          ．

9．如图是某冷饮店一天售出各种口味蛋糕数量的扇形统计图，其中售出奶油口味的雪糕150支，那么售出红豆口味雪糕的数量是        支．

10.平行四边形中，，则________°．

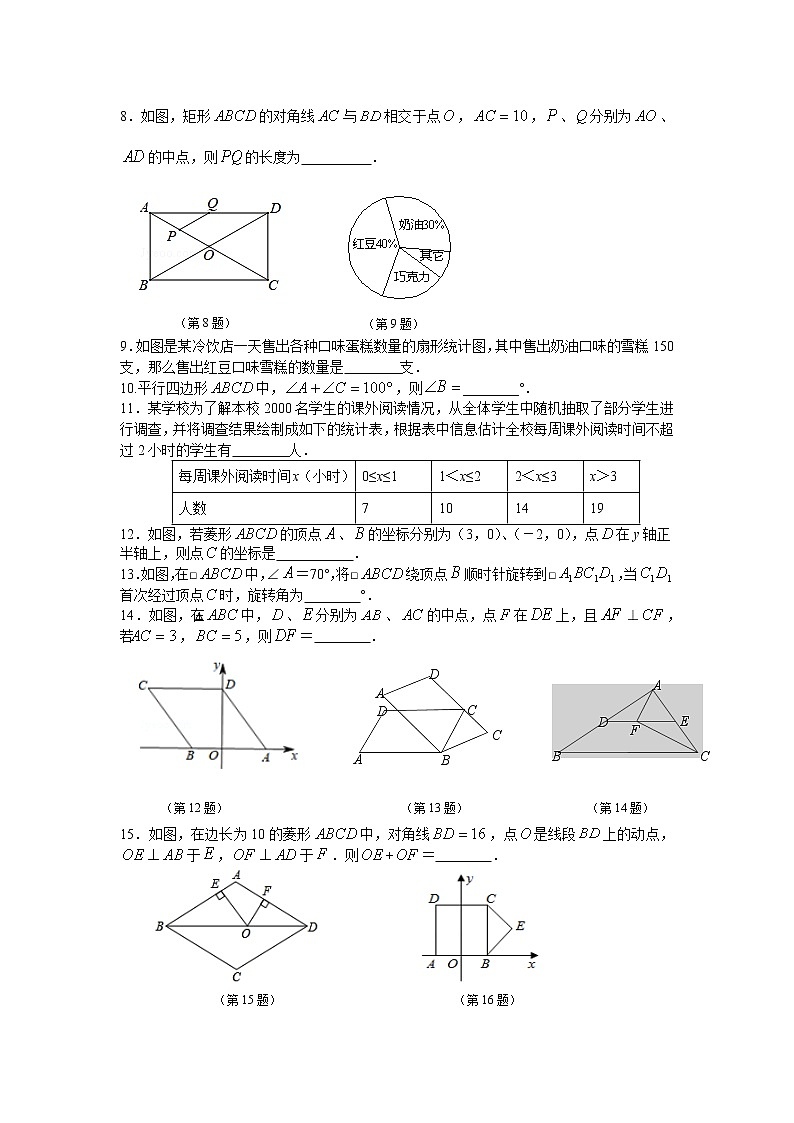
11．某学校为了解本校2000名学生的课外阅读情况，从全体学生中随机抽取了部分学生进行调查，并将调查结果绘制成如下的统计表，根据表中信息估计全校每周课外阅读时间不超过2小时的学生有        人．

12．如图，若菱形的顶点、的坐标分别为（3，0）、（－2，0），点在y轴正半轴上，则点的坐标是           ．

13．如图，在□中，∠＝70°，将□绕顶点顺时针旋转到□，当首次经过顶点时，旋转角为　    　°．

14．如图，在△中，、分别为、的中点，点在上，且⊥，若，，则＝　    　．

（第12题）                             （第13题）                    （第14题）                    

15．如图，在边长为10的菱形中，对角线，点是线段上的动点，于，于．则+＝　    　．

        （第15题）                             （第16题）

16．如图，在正方形中，顶点（﹣2，0），（2，0），将以为斜边的等腰直角与正方形组成的图形绕点顺时针旋转，每次旋转90°，则第10次旋转结束时，点的坐标为　     　．

三、解答题（本大题共有10小题，共102分，解答时应写出必要的文字说明、证明过程或演算步骤）

17．(9分)如图，在方格中，正方形被分成4个全等的直角三角形，请你用这4个全等的直角三角形在下面三个方格中分别重新拼接成一个新的四边形，要求新的四边形是中心对称图形.

18．（9分）4月22日是世界地球日，为了增强学生环保意识，某中学八年级举行了“环保知识竞赛”活动．为了了解本次竞赛情况，只抽取了部分学生的成绩（满分100分，得分均为正整数）进行统计，请你根据下面还未完成的频数分布表和频数分布直方图，解答下列问题：

（1）a＝　    　，b＝　    　．

（2）补全频数分布直方图；

（3）该校八年级有500名学生，估计八年级学生中竞赛成绩高于80分的有多少人？

19．（6分）一个不透明的袋子里装有黑白两种颜色的球共40只，这些球除颜色外都相同．小明从袋子中随机摸一个球，记下颜色后放回，不断重复，并绘制了如图所示的统计图，根据统计图提供的信息解决下列问题：

（1）估计袋中黑球的个数为　    　只；

（2）若小明又将一些相同的黑球放进了这个不透明的袋子里，然后再次进行摸球试验，当重复大量试验后，发现黑球的频率稳定在0.6左右，则小明后来放进了多少个黑球？

20．(8分) 某班从三名男生（含小强）和五名女生中选四名学生参加学校举行的“中华古诗文朗诵大赛”，规定女生选名．

（1）当为何值时，男生小强参加是必然事件？

（2）当为何值时，男生小强参加是随机事件？

21．（10分）如图，在中，D、E、F分别是、、的中点，连接、、．

（1）求证：四边形是平行四边形；

（2）若， ，求四边形的周长．

22．（10分）如图，在平行四边中，平分交于点，交于点，平分交于点．

（1）若，求的度数；

（2）求证：．

23．（12分）如图，在等腰直角中，，是由绕点按顺时针方向旋转得到的，连接、．

（1）求证：；

（2）当旋转角为40°时，求的度数．

24．（12分）如图，点为的边的中点，过点作，且，连接，．

（1）求证：；

（2）若，判断四边形的形状，并说明理由；

（3）若要使四边形为正方形，则应满足什么条件？（直接写出条件即可，不必证明）．

25．（12分）在矩形中， AB=10，BC=6，为射线上一点，将沿直线翻折至的位置，使点落在点处．

(1)若为边上一点．

①如图1，当点落在边上时，直接写出此时　    　；

②如图2，连接，若，则与有何数量关系？请说明理由；

(2)如果点在的延长线上，当为直角三角形时，求的长．

26．（14分）如图，已知点（a，0）、（b，0）满足（3a+b）2+|b﹣3|＝0．将线段先向上平移2个单位，再向右平移1个单位后得到线段，并连接、．

（1）请直接写出点和点的坐标；

（2）点从点出发，以每秒1个单位的速度向上平移运动．设运动时间为t秒，问：是否存在这样的t，使得四边形的面积等于8？若存在，请求出t的值；若不存在，请说明理由；

（3）在（2）的条件下，点从点出发的同时，点从点出发，以每秒2个单位的速度向左平移运动，设射线交y轴于点．设运动时间为t秒，问：S△EMD﹣S△OEN的值是否会发生变化？若不变，请求出它的值；若变化，请说明理由．

2021～2022学年度第二学期期中考试

八年级数学试题答案

一、选择题（本大题共6小题，每小题3分，共18分）

二、填空题：（本大题共10题，每空3分，共30分）

7．某校八年级学生的视力情况的全体    8．2.5      9．200      10．130°     11．680    

12．（﹣5，4）       13．40          14．1      15．9.6      16．（-4，-2）

四、解答题（本大题共有10小题，共102分，解答时应写出必要的文字说明、证明过程或演算步骤）

17． （9分）

18．（9分）

（1）12，0.24；·····················  (4分)

（2）略；··················(2分)

（3）500×(0.32＋0.24)=280(人）···················(3分)

答：八年级学生中竞赛成绩高于80分的约280人．

19．（6分）

（1）20················(3分)  （2）10················(3分)

20．（8分）

（1）；··············(4分)（2） ·················(4分)

21．（10分）

（1）∵D、E分别是AB、BC的中点，

∴DF是的中位线，

∴且，·····················(2分)

∵F是AC的中点，

∴，··························(3分)

∴，

∴四边形BEFD是平行四边形；·····················(5分)

（2）∵，F是AC的中点，

∴，,

在和中，

∴，···························(3分)

∴，

∵D、E分别是AB、BC的中点，

∴，

∴平行四边形BEFD是菱形，

∴四边形BEFD的周长．··································(5分)

22．（10分）

（1）解：∵四边形ABCD是平行四边形，

∴AD∥BC，

∴∠DAM＝∠AMB，

∵AE平分∠BAD，

∴∠BAM＝∠DAM，

∴∠AMB＝∠BAM，··································(2分)

∵∠ABC＝70°，∠AMB+∠BAM+∠ABC＝180°，

∴∠AMB＝（180°﹣∠ABC）＝×（180°﹣70°）＝55°；····················(5分)

（2）证明：∵四边形ABCD是平行四边形，

∴AB＝CD，AB∥CD，∠BAD＝∠BCD，

∴∠ABE＝∠CDF，

又∵AE平分∠BAD，CF平分∠BCD，

∴∠BAE＝∠BAD，∠DCF＝∠BCD，

∴∠BAE＝∠DCF，···································(2分)

在△ABE和△CDF中，

，

∴△ABE≌△CDF（ASA），

∴AE＝CF．···········································(5分)

23．（12分）

（1）证明：∵△ABE是由△ACF绕点A按顺时针方向旋转得到的，

∴△ABE≌△ACF，

∴AE＝AF，AB＝AC；∠BAE＝∠CAF，

∴∠BAC＝∠EAF，·····································(2分)

∵△ACF是等腰直角三角形，

∴AE＝AF＝AB＝AC，

∴△ACB≌△AFE（SAS），·······························(4分)

∴EF＝BC；············································(6分)

（2）解：∵旋转角为40°，

∴∠CAB＝40°，·······································(2分)

∵AB＝AC，

∴∠ACB＝70°，·······································(4分)

∵△ACF是等腰直角三角形，

∴∠ACF＝45°，

∴∠BCF＝∠ACB﹣∠ACF＝2···························(6分)

24．（12分）

（1）证明：∵D是BC的中点，

∴，∵，∴，···············(3分)

∵，

∴四边形ADCE是平行四边形，

∴；··························(6分)

（2）若，则四边形ADCE是矩形，理由如下：

∵，且D是BC的中点，

∴，

∴，························(3分)

∵四边形是平行四边形，

∴四边形是矩形；···························(6分)

（3），且．理由如下：

由（2）得：四边形是矩形，

∵，且D是BC的中点，

∴，，·························(3分)

∵，

∴，∴，

∴，∴，

∴四边形ADCE为正方形．········································(6分)

25．(12分)

解：（1）①CE =2；

 (4分)

②BC＝2BP，理由如下：

∵将△ABP沿直线AP翻折至△AEP的位置，

∴∠APB＝∠APE，PE＝BP，

∵CE∥AP，

∴∠CEP＝∠APE，∠ECP＝∠APB，

∴∠PEC＝∠ECP，

∴EP＝CP，

∴BP＝BC，

∴BC＝2BP； ·········································(8分)

（2）∵△PEC是直角三角形，

当∠EPC＝90°时，

∵∠EPC＝∠AEP＝∠B＝90°，且EP＝BP，

∴四边形ABPE是正方形，

∴PB＝AB＝10；·······································

当∠ECP＝90°时，

由翻折知AE＝AB＝10，根据勾股定理得DE＝8，

∴EC＝18，

设BP＝x，则PC＝x﹣6，

在Rt△ECP中，由勾股定理得：

182+（x﹣6）2＝x2，

解得x＝30，

∴PB＝30；

当∠PEC＝90°时，点P在线段BC上，

不符合题意，舍去，

综上：BP＝10或30．·····························(12分)

26．（14分）

（1）∵（3a+b）2+|b﹣3|＝0，

∴b＝3，a＝﹣1，

∴点A（﹣1，0），点B（3，0）；···················(4分)

（2）∵将线段AB先向上平移2个单位，再向右平移1个单位后得到线段CD，点A（﹣1，0），点B（3，0），

∴点C（0，2），点D（4，2），OA＝1，OB＝2，

∴OC＝2，CD＝4，

∴四边形OCDB的面积＝×（3+4）×2＝7，

∵四边形OMDB的面积等于8，

∴点M在点C上方，

∴四边形OMDB的面积＝四边形OCDB的面积+S△CDM＝7+×4×（t﹣2）＝8，

∴t＝2；················································(8分)

（3）S△EMD﹣S△OEN的值不会变化，

理由如下：如图1，当点N在线段OB上时，

∵S△EMD﹣S△OEN＝S四边形MDNO，

∴S△EMD﹣S△OEN＝S△MOD+S△OND＝×t×4+×（3﹣2t）×2＝3；············(11分)

如图2，当点N在x轴的负半轴时，

∵S△EMD﹣S△OEN＝（S△EMD+S△EOD）﹣（S△OEN+S△EOD），

∴S△EMD﹣S△OEN＝S△MOD﹣S△NOD＝×t×4﹣×（2t﹣3）×2＝3，

综上所述：S△EMD﹣S△OEN是定值3································(14分)