初中数学华师大版九年级上册24.2直角三角形的性质多媒体教学课件ppt

这是一份初中数学华师大版九年级上册24.2直角三角形的性质多媒体教学课件ppt，共19页。PPT课件主要包含了直角三角形，符号语言，基本图形，直角三角形的性质，试一试等内容，欢迎下载使用。
19.8 的性质
华东师大版九年级（上册）
直角三角形的两个锐角互余
在Rt △ABC中，∠C=90 °
∠A +∠B=90 °.
证明： ∵在 △ABC中， ∠A +∠B+∠C=180 ° （三角形的内角和是180 °）
又∵∠ C=90 °（已知）
∴ ∠A +∠B=90 °（等式性质）
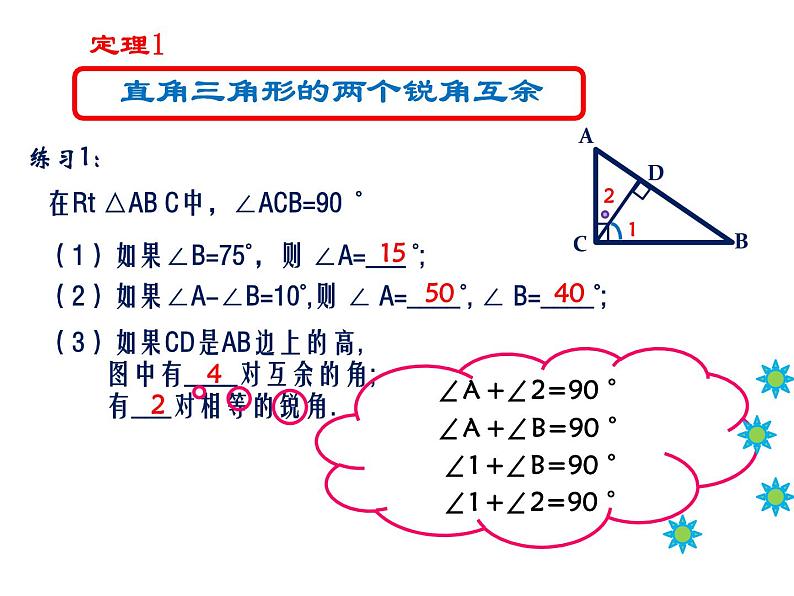
在Rt △AB C中，∠ACB=90 °
（1）如果∠B=75°，则 ∠A=___ °;
（2）如果∠A-∠B=10°,则 ∠ A=____°, ∠ B=____°;
（3）如果CD是AB边上的高, 图中有____对互余的角; 有___对相等的锐角.
∠A +∠2=90 °
∠A +∠B=90 °
∠1 +∠B=90 °
∠1 +∠2=90 °
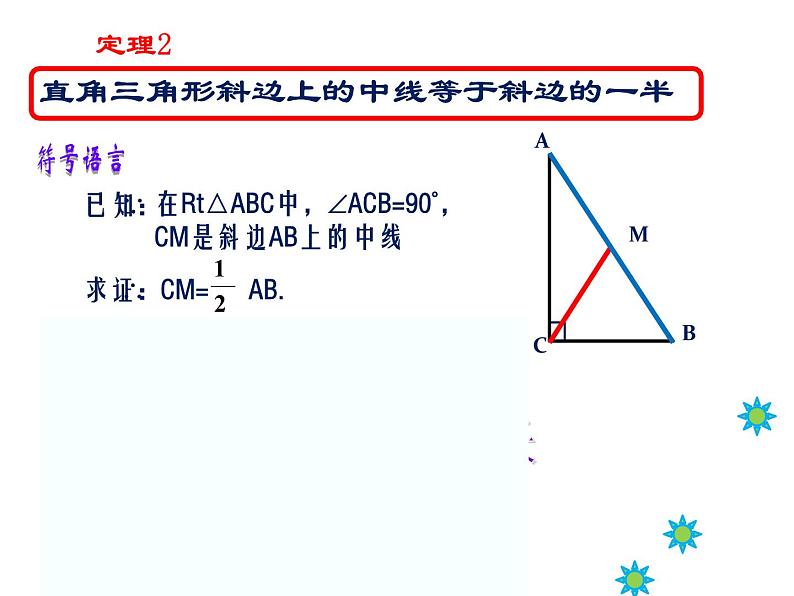
直角三角形斜边上的中线等于斜边的一半
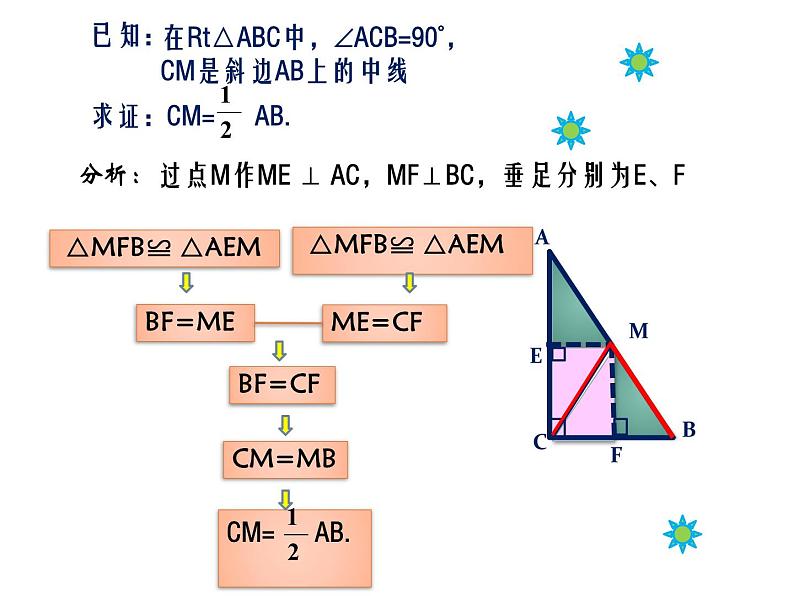
在Rt△ABC中，ACB=90°， CM是斜边AB上的中线
△MFB≌ △AEM
过点M作ME ⊥ AC，MF⊥BC，垂足分别为E、F
（直角三角形的两个锐角互余）
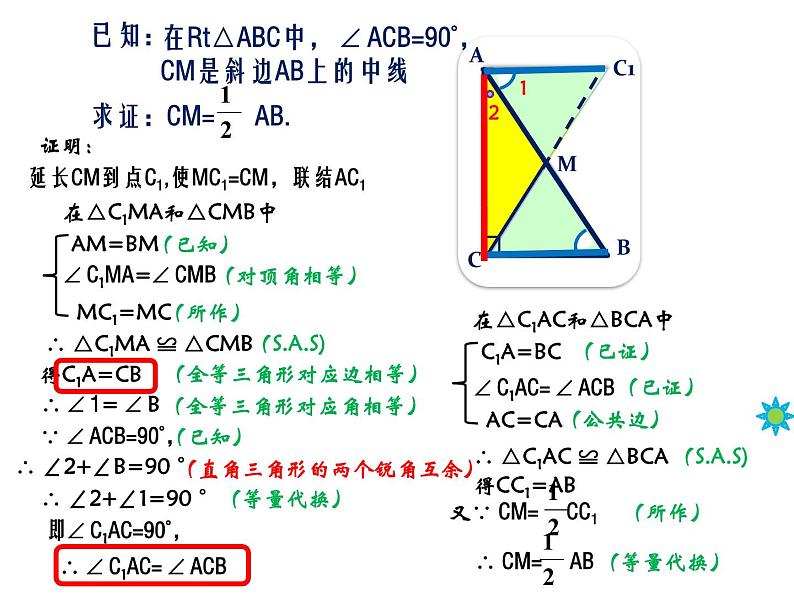
在Rt△ABC中，  ACB=90°， CM是斜边AB上的中线
在△C1MA和△CMB中
延长CM到点C1,使MC1=CM，联结AC1
 C1MA= CMB
∴ △C1MA ≌ △CMB
（全等三角形对应边相等）
∵  ACB=90°，
（全等三角形对应角相等）
∴ ∠2+∠B=90 °
∴ ∠2+∠1=90 °
即 C1AC=90°，
∴  C1AC=  ACB
在△C1AC和△BCA中
∴ △C1AC ≌ △BCA
 C1AC=  ACB
又∵ CM= CC1
∴ CM= AB
1、判断下列命题是真命题还是假命题：
（1）在△ACB中，CD是AB边上的中线，则CD= AB.（ ）
2、已知：在Rt△ABC中,∠ABC=90°，BM是AC边上的中线
（1）若BM=8，则AM=____，CM=____，AC=___；
（2）若∠C=25°，∠AMB=______°；
（3）若BD是AC边上的高，则与∠A相等的角有_____个.
已知：如图，在△ ABC中，AD ⊥ BC， E、F分别是AB、AC的中点，且DE=DF
等腰三角形底边上的中点
直角三角形斜边上的中点
如图1，在Rt △ ABC与Rt △ ACE中， ∠ ABC= ∠ AEC=90 °，点M是AC边上的中点，联结BM、EM、BE，点P是BE的中点. 求证：
∵ ∠ ABC= ∠ AEC=90 °
（直角三角形斜边上的中线等于斜边的一半）
又∵ P是BE边上的中点
（等腰三角形三线合一）
如图2，在Rt △ ABC与Rt △ ACE中， ∠ ABC= ∠ AEC=90 °，点M是AC边上的中点，联结BM、EM、BE，点P是BE的中点. 求证：MP ⊥ BE .
如图3，在△ACD中，AE、CB分别是边CD、AD上的高，M、 P分别是AC、BE的中点.求证：MP ⊥ BE .
∵ ∠AEC= ∠ABC=90 °
用右图的添线方法，完成性质定理2的证明 已知：在Rt△ABC中，ACB=90°， CM是斜边AB上的中线.
已知：如图，在Rt△ ABC中， ∠ C=90 ° ， AD ∥ BC， ∠CBE= ∠ABE .
求证：ED=2AB.
∠ ABE= ∠ AFB
∠ ABE= 2∠ CBE
作△AED边ED上的中线AF