初中数学北师大版七年级上册5.3 应用一元一次方程——水箱变高了教案配套ppt课件

这是一份初中数学北师大版七年级上册5.3 应用一元一次方程——水箱变高了教案配套ppt课件，共16页。PPT课件主要包含了导入新课，探究新知，π·22·4，π·162·x，应用举例，课堂小结，应用一元一次方程，图形等长变化，图形等积变化，随堂练习等内容，欢迎下载使用。

你听过这个故事吗？在1950年，业内处于领先地位的牙膏公司希望大幅度提高销售额，公司内部没有人想出奇招，外部有一个人却声称他能使销售额立马增长40%，并且售价10万美元．他的想法是：把牙膏的开口弄大一点．
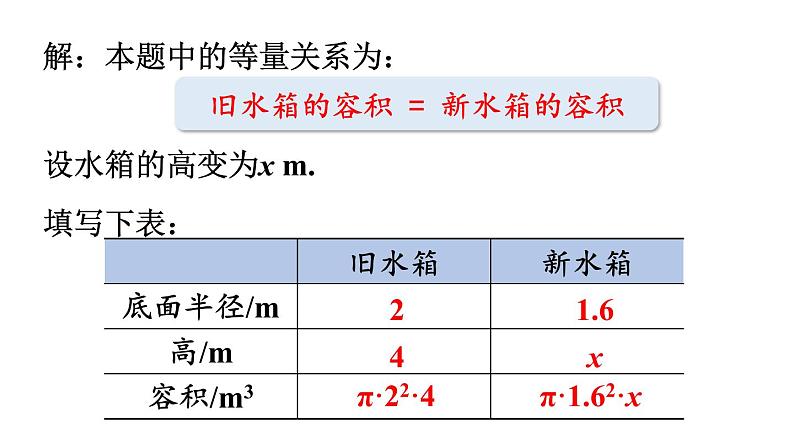
某居民楼顶有一个底面直径和高均为 4 m 的圆柱形储水箱. 现改楼进行维修改造，为减少楼顶原有储水箱的占地面积，需要将它的底面直径由 4 m 减少为 3.2 m. 那么在容积不变的前提下，水箱的高度将由原先的 4 m 变为多少米？
解：本题中的等量关系为：设水箱的高变为x m.填写下表：
旧水箱的容积 = 新水箱的容积
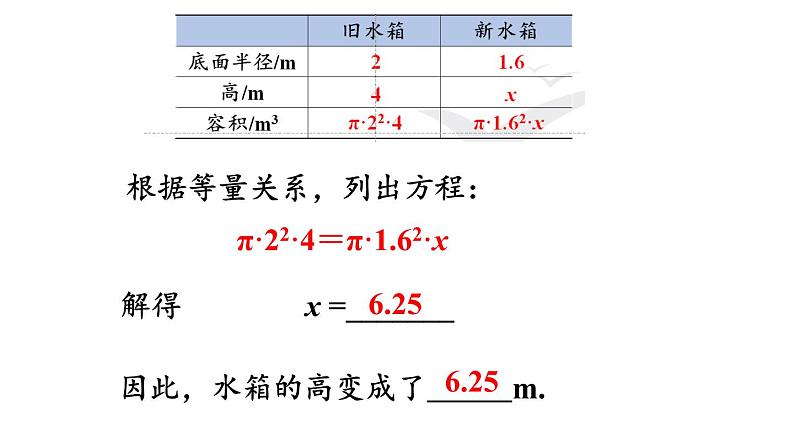
根据等量关系，列出方程：
解得 x =_______
因此，水箱的高变成了 m.
π·22·4＝π·1.62·x
例1 用一根长为 10 m 的铁丝围成一个长方形.
（1）使得该长方形的长比宽多 1.4 m，此时长方形的长、宽各为多少米？ （2）使得该长方形的长比宽多 0.8 m，此时长方形的长、宽各为多少米？它所围成的长方形与（1）中所围长方形相比，面积有什么变化？ （3）使得该长方形的长与宽相等，即围成一个正方形，此时正方形的边长是多少米？它所围成的面积与（2）中相比又有什么变化？
由题意知， 长方形的周长始终是不变的， 即长与宽的和为：10× = 5（m）.
解：（1）设此时长方形的宽为 x m， 则它的长为（x + 1.4）m.
根据题意，得 x + x + 1.4 = 10× .
解这个方程，得 x = 1.8.
1.8 + 1.4 = 3.2.
此时长方形的长为 3.2 m，宽为 1.8 m.
（2）设此时长方形的宽为 x m， 则它的长为（x + 0.8）m.
根据题意，得 x + x + 0.8 = 10× .
解这个方程，得 x = 2.1.
2.1 + 0.8 = 2.9.
此时长方形的长为 2.9 m，宽为 2.1 m，它所围成的面积为 2.9×2.1 = 6.09（m2），
（1）中长方形所围成的面积为 3.2×1.8 = 5.76（m2）.
此时长方形的面积比（1）中面积增大 6.09 – 5.76 = 0.33（m2）.
（3）设正方形的边长为 x m.
根据题意，得 x + x = 10× .
解这个方程，得 x = 2.5.
正方形的边长为 2.5 m，它所围成的面积为 2.5×2.5 = 6.25（m2），比（2）中面积增大 6.25 – 6.09 = 0.16（m2）.
例2 如图，小明将一个正方形纸片剪去一个宽为5 cm的长条后，再从剩下的长方形纸片上剪去一个宽6 cm的长条，如果两次剪下的长条面积正好相等，那么每一个长条的面积为多少？
解：设原来正方形纸的边长是x cm，则第一次剪下的长条的长是x cm，宽是5 cm，第二次剪下的长条的长是(x－5)cm，宽是6 cm.根据题意，得5x＝6(x－5).解得x＝30.则30×5＝150(cm2).答：每一个长条的面积为150 cm2.
应用一元一次方程解决实际问题的步骤
⑥检
②设
⑦答
1．用一根铁丝围成一个边长为9 cm的正方形，若用这根铁丝围成一个圆，则这个圆的面积为(　　)
2．把一个底面半径为10 cm，高为30 cm的圆柱形大杯中存满水，把水倒入一个底面直径为10 cm的圆柱形小杯中，刚好倒满12杯，则小杯的高为____cm.