








高中数学北师大版 (2019)选择性必修 第一册3.2 抛物线的简单几何性质评课课件ppt
展开第1课时 抛物线的简单几何性质(一)
第二章 3.2 抛物线的简单几何性质
学习目标
1.掌握抛物线的几何性质.
2.会利用抛物线的性质解决一些简单的抛物线问题.
导语
在上一节中,我们已经学习了抛物线的定义及其标准方程,类比椭圆和双曲线的几何性质的导学过程,这一节我们利用方程研究抛物线的几何性质.
内容索引
课时对点练
随堂演练
抛物线的简单几何性质
一
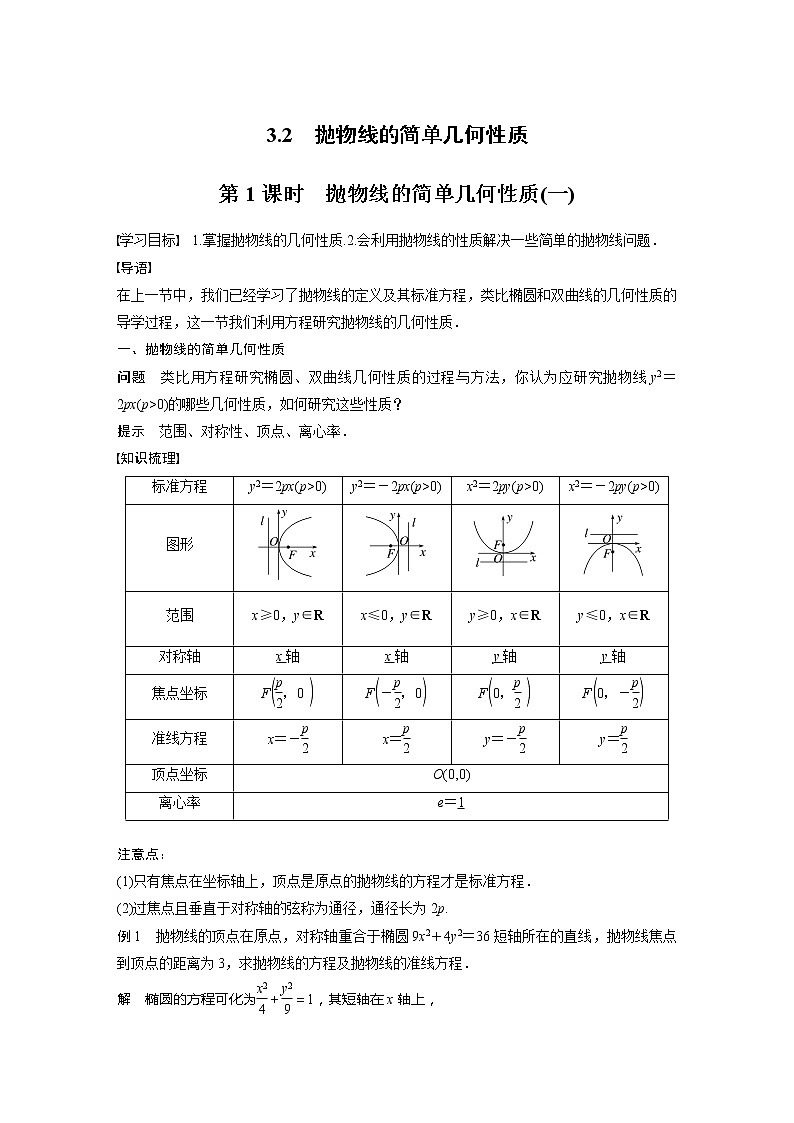
问题 类比用方程研究椭圆、双曲线几何性质的过程与方法,你认为应研究抛物线y2=2px(p>0)的哪些几何性质,如何研究这些性质?
提示 范围、对称性、顶点、离心率.
知识梳理
x
x
y
y
1
(1)只有焦点在坐标轴上,顶点是原点的抛物线的方程才是标准方程.(2)过焦点且垂直于对称轴的弦称为通径,通径长为2p.
注意点:
抛物线的顶点在原点,对称轴重合于椭圆9x2+4y2=36短轴所在的直线,抛物线焦点到顶点的距离为3,求抛物线的方程及抛物线的准线方程.
∴抛物线的对称轴为x轴,∴设抛物线的方程为y2=2px(p>0)或y2=-2px(p>0).∵抛物线的焦点到顶点的距离为3,
∴抛物线的标准方程为y2=12x或y2=-12x,其准线方程分别为x=-3和x=3.
把握三个要点确定抛物线的简单几何性质(1)开口:由抛物线标准方程看图象开口,关键是看准一次项是x还是y,一次项的系数是正还是负.(2)关系:顶点位于焦点与准线中间,准线垂直于对称轴.(3)定值:焦点到准线的距离为p;过焦点垂直于对称轴的弦(又称为通径)长为2p;离心率恒等于1.
反思感悟
边长为1的等边三角形AOB,O为坐标原点,AB⊥x轴,以O为顶点且过A,B的抛物线方程是
√
设抛物线方程为y2=ax(a≠0).
抛物线的几何性质的应用
二
(1)已知正三角形AOB的一个顶点O位于坐标原点,另外两个顶点A,B在抛物线y2=2px(p>0)上,求这个三角形的边长.
如图所示,设A(x1,y1),B(x2,y2),
又|OA|=|OB|,
整理得(x1-x2)(x1+x2+2p)=0.因为x1>0,x2>0,2p>0,所以x1=x2,
由此可得|y1|=|y2|,即线段AB关于x轴对称,由此得∠AOx=30°,
(2)已知A,B是抛物线y2=2px(p>0)上两点,O为坐标原点,若|OA|=|OB|,且△AOB的垂心恰是此抛物线的焦点,求直线AB的方程.
如图,设点A(x0,y0),由题意可知点B(x0,-y0),
∴AF⊥OB,∴kAF·kOB=-1,
反思感悟
利用抛物线的性质可以解决的问题(1)对称性:解决抛物线的内接三角形问题.(2)焦点、准线:解决与抛物线的定义有关的问题.(3)范围:解决与抛物线有关的最值问题.(4)焦点弦:解决焦点弦问题.
(1)(多选)设抛物线C:y2=2px(p>0)的焦点为F,点M在抛物线C上,|MF|=5,若y轴上存在点A(0,2),使得 =0,则p的值可以为A.2 B.4 C.6 D.8
√
√
由题意可得,以MF为直径的圆过点(0,2),
因为圆心是MF的中点,所以根据中点坐标公式可得,
据此可知该圆与y轴相切于点A(0,2),故圆心纵坐标为2,则M点纵坐标为4,
代入抛物线方程得p2-10p+16=0,所以p=2或p=8.
(2)抛物线y2=4x的焦点为F,准线为l,点A是抛物线上一点,且∠AFO=120°(O为坐标原点),AK⊥l,垂足为K,则△AKF的面积是______.
由抛物线方程可知F(1,0),准线l的方程为x=-1.如图,设A(x0,y0),过A作AH⊥x轴于H,在Rt△AFH中,|FH|=x0-1,由∠AFO=120°得∠AFH=60°,
课堂小结
1.知识清单: (1)抛物线的几何性质. (2)抛物线的几何性质的应用.2.方法归纳:待定系数法.3.常见误区:求抛物线方程时焦点的位置易判断失误.
随堂演练
1
2
3
4
√
1.对抛物线y=4x2,下列描述正确的是A.开口向上,焦点为(0,1)
1
2
3
4
由抛物线y=4x2,
2.(多选)以y轴为对称轴的抛物线的通径(过焦点且与对称轴垂直的弦)长为8,若抛物线的顶点在坐标原点,则其方程为A.y2=8x B.y2=-8xC.x2=8y D.x2=-8y
1
2
3
4
√
设抛物线方程为x2=2py或x2=-2py(p>0),由题意得2p=8.∴抛物线方程为x2=8y或x2=-8y.
√
1
2
3
4
√
3.若抛物线y2=x上一点P到准线的距离等于它到顶点的距离,则点P的坐标为
1
2
3
4
设抛物线的焦点为F,原点为O,P(x0,y0),由条件及抛物线的定义知,|PF|=|PO|,
1
2
3
4
4.已知抛物线y2=2px(p>0),直线x=m与抛物线交于A(x1,y1),B(x2,y2)两点,则y1+y2=____.
0
因为抛物线y2=2px(p>0)关于x轴对称,x=m与x轴垂直,故y1=-y2,即y1+y2=0.
课时对点练
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
由题意知,线段AB所在的直线方程为x=1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.以坐标轴为对称轴,以原点为顶点且过圆x2+y2-2x+6y+9=0的圆心的抛物线的方程是A.y=3x2或y=-3x2B.y=3x2C.y2=-9x或y=3x2D.y=-3x2或y2=9x
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
圆的方程可化为(x-1)2+(y+3)2=1,圆心为(1,-3),由题意可设抛物线方程为y2=2px(p>0)或x2=-2py(p>0).把(1,-3)代入得9=2p或1=6p,
即y2=9x或y=-3x2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.若抛物线y2=4x上一点P到x轴的距离为2 ,则点P到抛物线的焦点F的距离为A.4 B.5 C.6 D.7
√
由题意,知抛物线y2=4x的准线方程为x=-1,
∴点P到抛物线的准线的距离为3+1=4,∴点P到抛物线的焦点F的距离为4.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
5.已知抛物线y2=2px(p>0)的准线与曲线x2+y2-4x-5=0相切,则p的值为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
曲线的方程可化为(x-2)2+y2=9,其表示圆心为(2,0),半径为3的圆,
解得p=2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
6.(多选)若抛物线y2=8x上一点P到其焦点的距离为9,则点P的坐标为
根据抛物线y2=8x,知p=4,可知点P到其焦点的距离等于点P到其准线x=-2的距离,得xP=7,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.已知点A(-2,3)在抛物线C:y2=2px(p>0)的准线上,记抛物线C的焦点为F,则直线AF的斜率为______.
∵点A(-2,3)在抛物线C的准线上,
则焦点F的坐标为(2,0).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.已知F是抛物线C:y2=8x的焦点,M是C上一点,FM的延长线交y轴于点N.若M是FN的中点,则|FN|=____.
6
如图,过点M作MM′⊥y轴,垂足为M′,|OF|=2,∵M为FN的中点,|MM′|=1,
∴|MF|=3,∴|FN|=6.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.若抛物线的顶点在原点,开口向上,F为焦点,M为准线与y轴的交点,A为抛物线上一点,且|AM|= ,|AF|=3,求此抛物线的标准方程.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设所求抛物线的标准方程为x2=2py(p>0),
所以所求抛物线的标准方程为x2=4y或x2=8y.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.已知抛物线C的顶点在原点,焦点F在x轴的正半轴上,设A,B是抛物线C上的两个动点(AB不垂直于x轴),且|AF|+|BF|=8,线段AB的垂直平分线恒经过点Q(6,0),求抛物线的方程.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设抛物线的方程为y2=2px(p>0),
即x1+x2=8-p.∵Q(6,0)在线段AB的中垂线上,∴|QA|=|QB|,
设A(x1,y1),B(x2,y2),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴(x1-x2)(x1+x2-12+2p)=0.∵AB与x轴不垂直,∴x1≠x2.故x1+x2-12+2p=8-p-12+2p=0,即p=4.从而抛物线方程为y2=8x.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴点A的坐标为(1,±2).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.已知P是抛物线C:y2=2px(p>0)上的一点,F是抛物线C的焦点,O为坐标原点,若|PF|=2,∠PFO= ,则抛物线C的方程为A.y2=6x B.y2=2xC.y2=x D.y2=4x
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
过P向x轴作垂线,设垂足为Q,
将P点的坐标代入y2=2px,得p=3,故C的方程为y2=6x.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设M(x1,y1),
解得p=4,即抛物线的方程为y2=8x.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
要使△ABF为等边三角形,
解得p2=36,p=6.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
15.已知点A是抛物线x2=4y的对称轴与准线的交点,点B为抛物线的焦点,P在抛物线上且满足|PA|=m|PB|,当m取最大值时,点P恰好在以A,B为焦点的双曲线上,则该双曲线的离心率为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设点P(x,y),y≥0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.已知抛物线y2=8x.(1)求出该抛物线的顶点、焦点、准线方程、对称轴、变量x的范围;
抛物线y2=8x的顶点、焦点、准线方程、对称轴、变量x的范围分别为(0,0),(2,0),x=-2,x轴,x≥0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)以坐标原点O为顶点,作抛物线的内接等腰三角形OAB,|OA|=|OB|,若焦点F是△OAB的重心,求△OAB的周长.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
如图所示,由|OA|=|OB|可知AB⊥x轴,垂足为点M,又焦点F是△OAB的重心,
因为F(2,0),
所以M(3,0).故设A(3,m),代入y2=8x得m2=24,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
高中数学北师大版 (2019)选择性必修 第一册1 数学建模实例备课ppt课件: 这是一份高中数学北师大版 (2019)选择性必修 第一册1 数学建模实例备课ppt课件,文件包含第二章再练一课范围§1pptx、第二章再练一课范围§1docx等2份课件配套教学资源,其中PPT共40页, 欢迎下载使用。
新教材北师大版步步高选择性必修一【学案+同步课件】第二章 章末复习课: 这是一份新教材北师大版步步高选择性必修一【学案+同步课件】第二章 章末复习课,文件包含第二章章末复习课pptx、第二章章末复习课docx等2份课件配套教学资源,其中PPT共50页, 欢迎下载使用。
北师大版 (2019)选择性必修 第一册2.1 圆的标准方程教学演示免费课件ppt: 这是一份北师大版 (2019)选择性必修 第一册2.1 圆的标准方程教学演示免费课件ppt,文件包含第二章11第2课时椭圆的标准方程的综合问题pptx、第二章11第2课时椭圆的标准方程的综合问题docx等2份课件配套教学资源,其中PPT共60页, 欢迎下载使用。













