

北师大版九年级上册1 用树状图或表格求概率第2课时当堂达标检测题
展开1 用树状图或表格求概率
第2课时
必备知识·基础练
(打“√”或“×”)
1.在转盘型问题中,转出结果的可能性要相等.即所分割的各部分面积相等.( √ )
2.判断游戏公平性就要计算每个事件的概率,但是概率不相等游戏也可能公平.( × )
知识点1 转盘中的概率
1.(2020·衢州中考)如图是一个游戏转盘,自由转动转盘,当转盘停止转动后,指针落在数字“Ⅱ”所示区域内的概率是( A )
A. B. C. D.
【解析】由题可得,指针落在数字“Ⅱ”所示区域内的概率是:=.
2.(2020·河南中考)如图所示的转盘,被分成面积相等的四个扇形,分别涂有红、黄、蓝、绿四种颜色.固定指针,自由转动转盘两次,每次停止后,记下指针所指区域(指针指向区域分界线时,忽略不计)的颜色,则两次颜色相同的概率是____.
【解析】自由转动转盘两次,指针所指区域所有可能出现的情况如下:
第1次 第2次 | 红 | 黄 | 蓝 | 绿 |
红 | (红,红) | (黄,红) | (蓝,红) | (绿,红) |
黄 | (红,黄) | (黄,黄) | (蓝,黄) | (绿,黄) |
蓝 | (红,蓝) | (黄,蓝) | (蓝,蓝) | (绿,蓝) |
绿 | (红,绿) | (黄,绿) | (蓝,绿) | (绿,绿) |
共有16种等可能出现的结果,其中两次颜色相同的有4种,∴P(两次颜色相同)==.
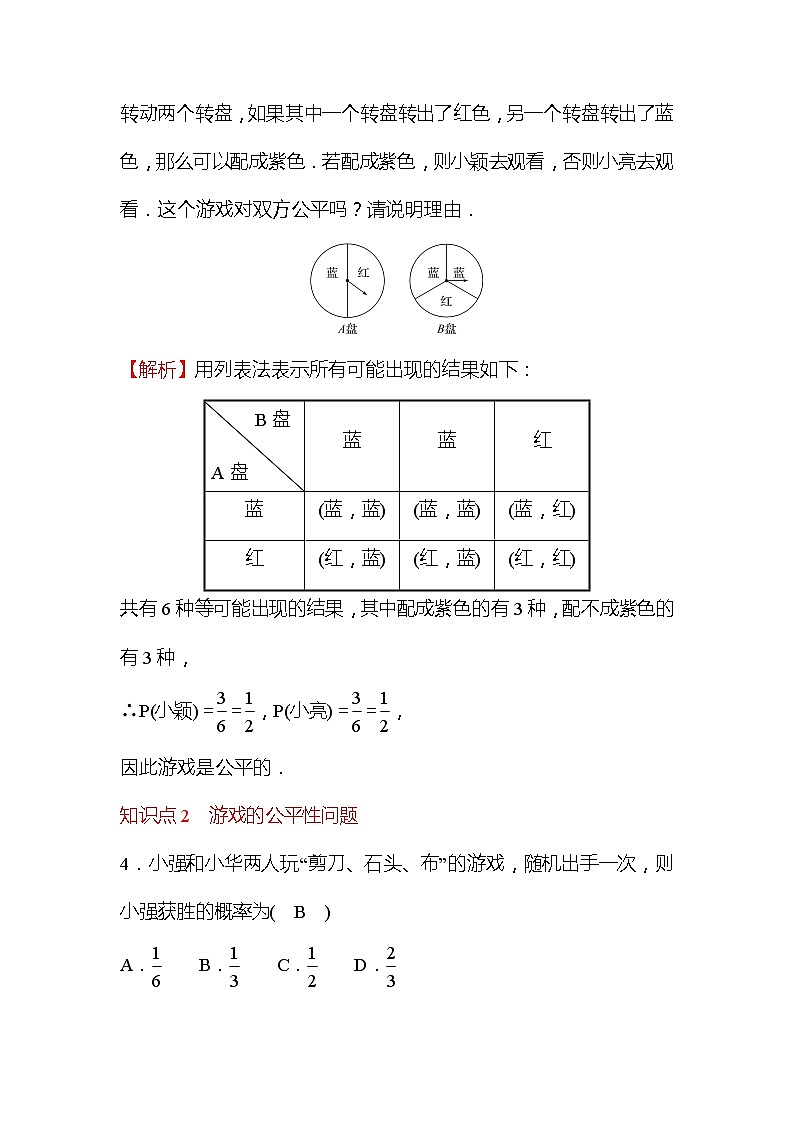
3.(2020·青岛中考)小颖和小亮都想去观看“垃圾分类”宣传演出,但只有一张入场券,于是他们设计了一个“配紫色”游戏:A,B是两个可以自由转动的转盘,每个转盘都被分成面积相等的几个扇形.同时转动两个转盘,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,那么可以配成紫色.若配成紫色,则小颖去观看,否则小亮去观看.这个游戏对双方公平吗?请说明理由.
【解析】用列表法表示所有可能出现的结果如下:
B盘 A盘 | 蓝 | 蓝 | 红 |
蓝 | (蓝,蓝) | (蓝,蓝) | (蓝,红) |
红 | (红,蓝) | (红,蓝) | (红,红) |
共有6种等可能出现的结果,其中配成紫色的有3种,配不成紫色的有3种,
∴P(小颖)==,P(小亮)==,
因此游戏是公平的.
知识点2 游戏的公平性问题
4.小强和小华两人玩“剪刀、石头、布”的游戏,随机出手一次,则小强获胜的概率为( B )
A. B. C. D.
【解析】画树状图得:
∵共有9种等可能的结果,小强获胜的情况数是3种,∴小强获胜的概率是=.
5.(2021·德州质检)甲、乙是两个不透明的纸箱,甲中有三张标有数字,,1的卡片,乙中有三张标有数字1,2,3的卡片,卡片除所标数字外无其他差别,现制定一个游戏规则:从甲中任取一张卡片,将其数字记为a,从乙中任取一张卡片,将其数字记为b.若a,b能使关于x的一元二次方程ax2+bx+1=0有两个不相等的实数根,则甲获胜;否则乙获胜.则乙获胜的概率为( C )
A. B. C. D.
【解析】画树状图如下:
由图可知,共有9种等可能的结果,其中能使乙获胜的有4种,∴乙获胜的概率为.
6.(2020·昆明中考)有一个可自由转动的转盘,被分成了三个大小相同的扇形,分别标有数字2,4,6;另有一个不透明的瓶子,装有分别标有数字1,3,5的三个完全相同的小球.小杰先转动一次转盘,停止后记下指针指向的数字(若指针指在分界线上则重转),小玉再从瓶子中随机取出一个小球,记下小球上的数字.
(1)请用列表或画树状图的方法(选其中一种)表示出所有可能出现的结果;
(2)若得到的两数字之和是3的倍数,则小杰贏;若得到的两数字之和是7的倍数,则小玉赢,此游戏公平吗?为什么?
【解析】(1)用列表法表示所有可能出现的结果情况如下:
转盘 摸球 | 2 | 4 | 6 |
1 | 2+1 | 4+1 | 6+1 |
3 | 2+3 | 4+3 | 6+3 |
5 | 2+5 | 4+5 | 6+5 |
(2)由(1)的表格可知,共有9种等可能出现的结果,其中“和为3的倍数”的有3种,“和为7的倍数”的有3种,∴P(小杰胜)==,P(小玉胜)==,
因此游戏是公平的.
关键能力·综合练
1.(2021·郑州模拟)现有三张分别标有数字1,2,3的牌,它们除数字外完全相同,把牌背面朝上洗匀后,甲、乙两人进行摸牌游戏.甲从中随机抽取一张,记下数字后放回洗匀,乙再从中随机抽取一张,若两人抽取的数字之和为偶数,则甲胜,否则乙胜.甲获胜的概率是( D )
A. B. C. D.
【解析】画树状图为:
共有9种等可能的结果,其中两人抽取的数字之和为偶数的有5种结果,所以甲获胜的概率为.
2.(2021·青岛质检)如图所示,每个转盘被分成相等的3个扇形,甲、乙两人利用它做游戏.同时转动两个转盘,如果两个指针所停区域的颜色相同,则甲获胜,如果两个指针所停区域的颜色不同,则乙获胜.则甲、乙获胜的概率分别是( D )
A., B.,
C., D.,
【解析】如图所示:
共有9种等可能的情况,颜色相同的情况有3种,所以甲获胜的概率为=;颜色不同的情况有6种,所以乙获胜的概率为=.
3.(2021·柳州质检)小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为( A )
A. B. C. D.
【解析】画树状图如图:
共有25个等可能的结果,两人出拳的手指数之和为偶数的结果有13个,
∴小李获胜的概率为.
4.(2020·铜仁中考)从-2,-1,2三个数中任取两个不同的数,作为点的坐标,则该点在第三象限的概率等于____.
【解析】画树状图如下:
共有6种等可能的情况,该点在第三象限有(-2,-1)和(-1,-2)这2种情况,
∴该点在第三象限的概率等于=.
5.(2020·云南中考)甲、乙两个家庭来到以“生态资源,绿色旅游”为产业的美丽云南,各自随机选择到大理、丽江、西双版纳三个城市中的一个城市旅游.假设这两个家庭选择到哪个城市旅游不受任何因素影响,上述三个城市中的每一个被选到的可能性相同,甲、乙两个家庭选择到上述三个城市中的同一个城市旅游的概率为P.
(1)直接写出甲家庭选择到大理旅游的概率;
(2)用列表法或树状图法(树状图也称树形图)中的一种方法,求P的值.
【解析】(1)甲家庭选择到大理旅游的概率为.
(2)记到大理、丽江、西双版纳三个城市旅游分别为A,B,C,
列表得:
| A | B | C |
A | (A,A) | (A,B) | (A,C) |
B | (B,A) | (B,B) | (B,C) |
C | (C,A) | (C,B) | (C,C) |
由表格可知,共有9种等可能的结果,其中甲、乙两个家庭选择到上述三个城市中的同一个城市旅游的有3种结果,所以甲、乙两个家庭选择到上述三个城市中的同一个城市旅游的概率P==.
6.(2020·扬州中考)防疫期间,全市所有学校都严格落实测体温进校园的防控要求.某校开设了A,B,C三个测温通道,某天早晨,该校小明和小丽两位同学将随机通过测温通道进入校园.
(1)小明从A测温通道通过的概率是______;
(2)利用画树状图或列表的方法,求小明和小丽从同一个测温通道通过的概率.
【解析】(1)小明从A测温通道通过的概率是.
答案:
(2)列表格如下:
| A | B | C |
A | A,A | B,A | C,A |
B | A,B | B,B | C,B |
C | A,C | B,C | C,C |
由表可知,共有9种等可能的结果,其中小明和小丽从同一个测温通道通过的结果有3种,所以小明和小丽从同一个测温通道通过的概率为=.
7.(素养提升题)在四边形ABCD中,有下列条件:
①ABCD;②ADBC;③AC=BD;④AC⊥BD.
(1)从中任选一个作为已知条件,能判定四边形ABCD是平行四边形的概率是__________.
(2)从中任选两个作为已知条件,请用画树状图或列表的方法表示能判定四边形ABCD是矩形的概率,并判断能判定四边形ABCD是矩形和是菱形的概率是否相等.
【解析】(1)①或②能判定四边形ABCD是平行四边形,故所求概率为=.
答案:
(2)画树状图为:
由树状图得知,从中任选两个作为已知条件共有12种等可能的结果,能判定四边形ABCD是矩形的有4种,能判定四边形ABCD是菱形的有4种,∴能判定四边形ABCD是矩形的概率是=,能判定四边形ABCD是菱形的概率是=,∴能判定四边形ABCD是矩形和是菱形的概率相等.
易错点 忽视等可能的前提条件.
【案例】(2021·青岛期中)用如图所示的两个转盘进行“配紫色”游戏,配得紫色的概率是( C )
A. B. C. D.1
【解析】将第2个圆中蓝色部分划分为圆心角为120°的两部分:蓝1、蓝2,
画树状图如下:
由树状图可知,共有6种等可能的结果,其中能配成紫色(红色和蓝色)的有3种结果,
∴配得紫色的概率是=.
关闭Word文档返回原板块
【课时训练】北师大版数学九年级上册--3.1 用树状图或表格求概率(pdf版,含答案): 这是一份【课时训练】北师大版数学九年级上册--3.1 用树状图或表格求概率(pdf版,含答案),文件包含课时训练参考答案全册pdf、31用树状图或表格求概率pdf等2份试卷配套教学资源,其中试卷共22页, 欢迎下载使用。
数学1 用树状图或表格求概率第1课时一课一练: 这是一份数学1 用树状图或表格求概率第1课时一课一练,共13页。
初中数学北师大版九年级上册1 用树状图或表格求概率第1课时课后作业题: 这是一份初中数学北师大版九年级上册1 用树状图或表格求概率第1课时课后作业题,共4页。试卷主要包含了画树状图或列表求概率的条件等内容,欢迎下载使用。













