

数学1 用树状图或表格求概率第1课时一课一练
展开第三章 概率的进一步认识
1 用树状图或表格求概率
第1课时
必备知识·基础练
(打“√”或“×”)
1.当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为不重不漏地列出所有可能的结果,通常采用列表法.( √ )
2.列表法求随机事件发生的概率时,列表时数据或事件的顺序混淆也没关系.( × )
3.当一次试验要涉及2个以内因素时,为了不重不漏地列出所有可能的结果,通常采用树状图.( × )
4.求随机事件的概率涉及两个因素的问题时只能用列表法不能用画树状图法.( × )
5.用树状图计算概率时,必须保证两步之间的相互独立性.( √ )
知识点1 画树状图法求概率
1.(2021·天津期中)一个不透明的袋子中装有3个白球,2个黑球,它们除了颜色外都相同.将球摇匀后,从中随机摸出一个球,记下颜色后放回,再随机摸出一个球.两次摸到的球颜色相同的概率是( B )
A. B. C. D.
【解析】画树状图如图:
共有25种等可能的结果,两次摸出的球颜色相同有13种情况,∴两次摸出的球颜色相同的概率为.
2.(2021·兰州期中)小明制作了3张卡片,分别涂上了红、黑、蓝三种颜色.从这三张卡片中随机抽取两张恰好是“红蓝”的概率是( C )
A. B. C. D.
【解析】画树状图如图:
共有6个等可能的结果,从这三张卡片中随机抽取两张恰好是“红蓝”的结果有2个,
∴从这三张卡片中随机抽取两张恰好是“红蓝”的概率==.
3.(2020·重庆中考A卷)现有四张正面分别标有数字-1,1,2,3的不透明卡片,它们除数字外其余完全相同,将它们背面朝上洗均匀,随机抽取一张,记下数字后放回,背面朝上洗均匀,再随机抽取一张记下数字,前后两次抽取的数字分别记为m,n.则点P(m,n)在第二象限的概率为____.
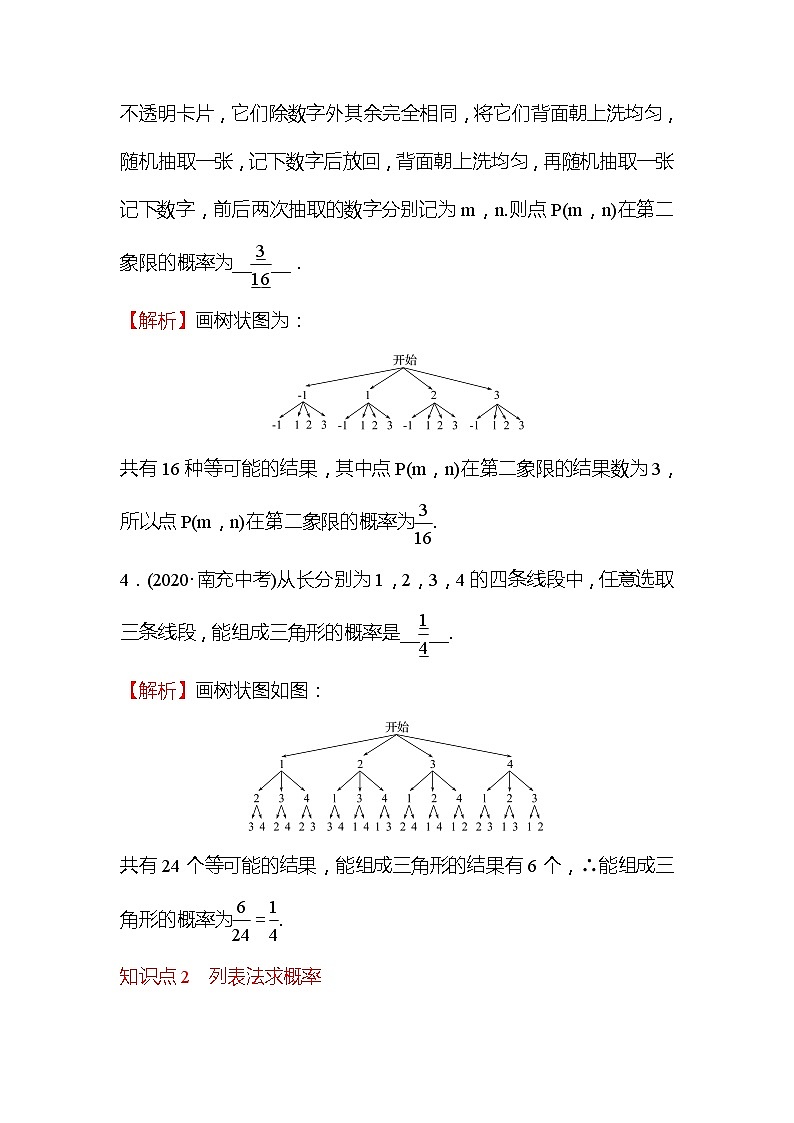
【解析】画树状图为:
共有16种等可能的结果,其中点P(m,n)在第二象限的结果数为3,所以点P(m,n)在第二象限的概率为.
4.(2020·南充中考)从长分别为1,2,3,4的四条线段中,任意选取三条线段,能组成三角形的概率是____.
【解析】画树状图如图:
共有24个等可能的结果,能组成三角形的结果有6个,∴能组成三角形的概率为=.
知识点2 列表法求概率
5.(2021·西藏期中)现有两道数学选择题,它们都是单选题,并且都含有A,B,C,D四个选项,瞎猜这两道题,这两道题恰好全部猜对的概率是( D )
A. B. C. D.
【解析】用列表法表示所有可能出现的结果情况如下:
第1题 第2题 | A | B | C | D |
A | (A,A) | (B,A) | (C,A) | (D,A) |
B | (A,B) | (B,B) | (C,B) | (D,B) |
C | (A,C) | (B,C) | (C,C) | (D,C) |
D | (A,D) | (B,D) | (C,D) | (D,D) |
共有16种等可能出现的结果,其中两道题恰好全部猜对的只有1种,
所以,两道题恰好全部猜对的概率为.
6.(2020·枣庄中考)不透明布袋中装有除颜色外没有其他区别的1个红球和2个白球,搅匀后从中摸出一个球,放回搅匀,再摸出一个球,两次都摸出白球的概率是( A )
A. B. C. D.
【解析】用列表法表示所有可能出现的情况如下:
第1球 第2球 | 红 | 白 | 白 |
红 | (红,红) | (白,红) | (白,红) |
白 | (红,白) | (白,白) | (白,白) |
白 | (红,白) | (白,白) | (白,白) |
共有9种等可能出现的结果,其中两次都是白球的有4种,∴P(两次都是白球)=.
7.(2021·重庆期中)小白有两张卡片,分别标有数字1,2;小黄有三张卡片,分别标有数字3,4,5.两人各自随机地取出一张卡片,取出的两张卡片上数字之积为奇数的概率是____.
【解析】用列表法表示所有可能出现的结果情况如下:
共有6种等可能出现的情况,其中数字之积为奇数的有2种,所以,取出的两张卡片上数字之积为奇数的概率为=.
8.(2020·徐州中考)小红的爸爸积极参加社区抗疫志愿服务工作.根据社区的安排,志愿者被随机分到A组(体温检测)、B组(便民代购)、C组(环境消杀).
(1)小红的爸爸被分到B组的概率是________;
(2)某中学王老师也参加了该社区的志愿者队伍,他和小红爸爸被分到同一组的概率是多少?(请用画树状图或列表的方法写出分析过程)
【解析】(1)共有3种等可能出现的结果,被分到“B组”的有1种,因此被分到“B组”的概率为.
(2)用列表法表示所有可能出现的结果如表:
小红爸爸 王老师 | A | B | C |
A | (A,A) | (B,A) | (C,A) |
B | (A,B) | (B,B) | (C,B) |
C | (A,C) | (B,C) | (C,C) |
共有9种等可能出现的结果,其中“他与小红的爸爸”在同一组的有3种,∴P(他与小红爸爸在同一组)==.
关键能力·综合练
1.(2020·牡丹江中考)在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.若随机摸出一个小球后不放回,再随机摸出一个小球,则两次取出小球标号的和等于5的概率为( C )
A. B. C. D.
【解析】用列表法表示所有可能出现的结果情况如下:
第1次 第2次 | 1 | 2 | 3 | 4 |
1 |
| 3 | 4 | 5 |
2 | 3 |
| 5 | 6 |
3 | 4 | 5 |
| 7 |
4 | 5 | 6 | 7 |
|
共有12种等可能出现的结果,其中“和为5”的有4种,∴P(和为5)==.
2.(2021·河南期中)有一首《对子歌》中唱到:天对地,雨对风,大陆对长空.现将“天,雨,大,空”四个字书写在材质、大小完全相同的卡片上,在暗箱搅匀后,随机抽取两张,恰为“天”“空”二字的概率为( D )
A. B. C. D.
【解析】画树状图如图:
由树状图知,共有12种等可能的结果,其中恰为“天”“空”的有2种结果,
∴恰为“天”“空”的概率为=.
3.(2020·咸宁中考)某校开展以“我和我的祖国”为主题的“大合唱”活动,七年级准备从小明、小东、小聪三名男生和小红、小慧两名女生中各随机选出一名男生和一名女生担任领唱,则小聪和小慧被同时选中的概率是____.
【解析】利用列表法表示所有可能出现的结果如表:
男生 女生 | 小明 | 小东 | 小聪 |
小红 | (小明,小红) | (小东,小红) | (小聪,小红) |
小慧 | (小明,小慧) | (小东,小慧) | (小聪,小慧) |
共有6种等可能出现的结果,其中小聪和小慧同时被选中的有1种,∴P(小聪和小慧同时被选中)=.
4.(2020·大庆中考)两个人做游戏:每个人都从-1,0,1这三个整数中随机选择一个写在纸上,则两人所写整数的绝对值相等的概率为____.
【解析】画树状图为:
共有9种等可能的结果,其中两数的绝对值相等的结果数为5,所以两人所写整数的绝对值相等的概率为.
5.小明与甲、乙两人一起玩“手心手背”的游戏.他们约定:如果三人中仅有一人出“手心”或“手背”,则这个人获胜;如果三人都出“手心”或“手背”,则不分胜负,那么在一个回合中,如果小明出“手心”,求他获胜的概率是多少?(请用“画树状图”或“列表”等方法写出分析过程)
【解析】画树状图得:
∵共有4种等可能的结果,在一个回合中,如果小明出“手心”,则他获胜的有1种情况,
∴他获胜的概率是.
6.(2021·常熟期中)小红和父母计划寒假期间从A:拙政园、B:狮子林、C:上方山森林动物世界、D:天平山风景名胜区这4个景点中随机选择景点游玩.
(1)若小红一家从中随机选择一个景点游玩,则选中C:上方山森林动物世界的概率为________;
(2)若小红一家从中随机选择两个景点游玩,请用列举法(画树状图或列表)求选中A,C两个景点的概率.
【解析】(1)∵共有4个景点,分别是A:拙政园、B:狮子林、C:上方山森林动物世界、D:天平山风景名胜区,
∴选中C:上方山森林动物世界的概率为.
答案:
(2)用表格列出所有可能的结果:
| A | B | C | D |
A |
| (A,B) | (A,C) | (A,D) |
B | (B,A) |
| (B,C) | (B,D) |
C | (C,A) | (C,B) |
| (C,D) |
D | (D,A) | (D,B) | (D,C) |
|
共有12种等可能的结果,其中选择A,C两个景点的有2种,选中A,C两个景点的概率是=.
7.(素养提升题)(2020·盐城中考)生活在数字时代的我们,很多场合用二维码(如图①)来表示不同的信息,类似地,可通过在矩形网格中,对每一个小方格涂色或不涂色所得的图形来表示不同的信息,例如:网格中只有一个小方格,如图②,通过涂色或不涂色可表示两个不同的信息.
(1)用树状图或列表格的方法,求图③可表示不同信息的总个数;(图中标号1、2表示两个不同位置的小方格,下同)
(2)图④为2×2的网格图,它可表示不同信息的总个数为________;
(3)某校需要给每位师生制作一张“校园出入证”,准备在证件的右下角采用n×n的网格图来表示个人身份信息,若该校师生共492人,则n的最小值为________.
【解析】(1)画树状图如图:
共有4种等可能结果.∴题图③可表示不同信息的总个数为4.
(2)画树状图如图:
共有16种等可能结果.
答案:16
(3)由题图②得:当n=1时,21=2,
由题图④得:当n=2时,22×22=16,
∴n=3时,23×23×23=512,
∵16<492<512,
∴n的最小值为3.
答案:3
易错点 在分析可能的结果时容易忽略放回与不放回.
【案例1】(2020·杭州中考)一个仅装有球的不透明布袋里共有4个球(只有编号不同),编号分别为1,2,3,5.从中任意摸出一个球,记下编号后放回,搅匀,再任意摸出一个球,则两次摸出的球的编号之和为偶数的概率是____.
【解析】根据题意画图如下:
共有16种等可能情况数,其中两次摸出的球的编号之和为偶数的有10种,
则两次摸出的球的编号之和为偶数的概率是=.
【案例2】(2021·重庆质检)有四张正面分别标有数字-1,1,2,4的不透明卡片,除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任意抽取一张,将该卡片正面上的数字记为a;放回后再从中任意抽取一张,将该卡片正面朝上的数字记为b,则使关于x的一元二次方程ax2+bx+1=0有实根的概率为____.
【解析】根据题意画图如下:
共有16种等可能的情况数,其中使关于x的一元二次方程ax2+bx+1=0有实根的有8种,
则使关于x的一元二次方程ax2+bx+1=0有实根的概率为=.
关闭Word文档返回原板块
初中数学北师大版九年级上册1 用树状图或表格求概率第1课时课后作业题: 这是一份初中数学北师大版九年级上册1 用树状图或表格求概率第1课时课后作业题,共4页。试卷主要包含了画树状图或列表求概率的条件等内容,欢迎下载使用。
北师大版九年级上册第三章 概率的进一步认识1 用树状图或表格求概率第2课时练习题: 这是一份北师大版九年级上册第三章 概率的进一步认识1 用树状图或表格求概率第2课时练习题,共4页。
初中数学北师大版九年级上册第三章 概率的进一步认识1 用树状图或表格求概率第1课时测试题: 这是一份初中数学北师大版九年级上册第三章 概率的进一步认识1 用树状图或表格求概率第1课时测试题,共7页。













