初中人教版第二十四章 圆综合与测试单元测试同步达标检测题

这是一份初中人教版第二十四章 圆综合与测试单元测试同步达标检测题，共20页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
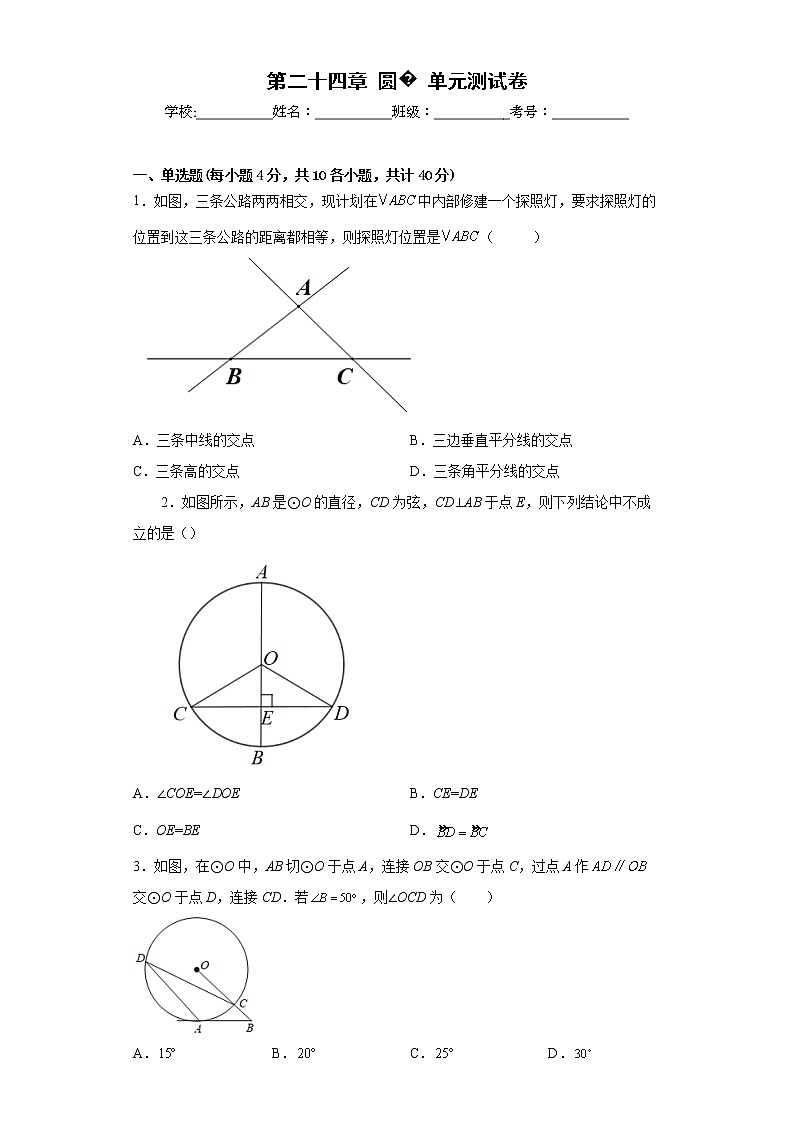
第二十四章 圆� 单元测试卷学校:___________姓名：___________班级：___________考号：___________ 一、单选题(每小题4分，共10各小题，共计40分)1．如图，三条公路两两相交，现计划在中内部修建一个探照灯，要求探照灯的位置到这三条公路的距离都相等，则探照灯位置是（       ）A．三条中线的交点 B．三边垂直平分线的交点C．三条高的交点 D．三条角平分线的交点2．如图所示，AB是⊙O的直径，CD为弦，CD⊥AB于点E，则下列结论中不成立的是（）A．∠COE=∠DOE B．CE=DEC．OE=BE D．3．如图，在⊙O中，AB切⊙O于点A，连接OB交⊙O于点C，过点A作交⊙O于点D，连接CD．若，则∠OCD为（　　）A． B． C． D．4．如图，以点为圆心的两个同心圆把以为半径的大圆的面积三等分，这两个圆的半径分别为，．则的值是（       ） A． B． C． D．5．如图，ABCD为圆内接四边形，若∠A＝60°，则∠C等于（   ）A．30° B．60°C．120° D．300°6．如图，在⊙O中，点A是的中点，∠ADC＝24°，则∠AOB的度数是（　　）A．24° B．26° C．48° D．66°7．若的直径为10，点到圆心的距离为6，那么点与的位置关系是（       ）A．点在外 B．点在上 C．点在内 D．不能确定8．如图，的弦垂直于，为垂足，，，且，则圆心到的距离是（       ）A．2 B． C． D．9．如图所示，在中，，，则的度数是（       ）A．55° B．110° C．125° D．150°10．如图，AB为⊙O的直径，点C在⊙O上，若∠OCA＝50°，AB＝4，则的长为（　　）A．π B．π C．π D．π 二、填空题(每小题5分，共5各小题，共计25分)11．如图，在平面直角坐标系中，点为坐标原点，点在第一象限，过原点，且与轴、轴交于点A，，点A的坐标为，的直径为10．则点的坐标为______．12．如图，的半径为2cm，正六边形内接于，则图中阴影部分面积为______．13．如图正方形的边长为1，分别以正方形的两个相对顶点为圆心，以1为半径画弧，则图中阴影部分的面积是______（用含有的式子表示）．14．一只小猫在距墙面4米，距地面2米的架子上，紧紧盯住了斜靠墙的梯子中点处的一只老鼠，聪明的小猫准备在梯子下滑时，在与老鼠距离最小时捕食．如图所示，把墙面、地面、梯子、猫和老鼠都理想化为同一平面内的线或点，模型如图，，梯子的两端M，N分别在墙面和地面上，猫所处位置为点D，老鼠抽象为点E，已知梯子长为4米，在梯子滑动过程中，猫与老鼠的距离的最小值为_____________ 米．15．如图，在矩形中，，，以为边在其右侧作等边，再以点为圆心，线段为半径画弧，则图中阴影部分的面积是__________． 三、解答题(16、17、18题9分，19题8分，共计35分)16．如图，中，，AC和BC分别与相切于E，F两点，AB经过上的点M，且．(1)求证：AB是的切线；(2)若，求的半径．17．如图，在△ABC中，AB＝AC， ，以AB为直径作⊙O分别交BC，AC于点D，E，连接AD，过点D作⊙O的切线交AC于点F．(1)试猜想和的数量关系，并说明理由．(2)若，求AF的长．18．用铁皮制作圆锥形容器盖，其尺寸要求如图所示 ．  (1)求圆锥的高；(2)求所需铁皮的面积（结果保留）．19．如图1，在平面直角坐标系xOy中，抛物线y＝ax2＋bx经过点（－2，5），且与直线y=－x在第二象限交于点A，过点A作AB⊥x轴，垂足为点B（－4，0）．若P是直线OA上方该抛物线上的一个动点，过点P作PC⊥x轴于点C，交OA于点D，连接OP，PA．(1)求抛物线的解析式；(2)求△AOP的面积S的最大值；(3)连接PB交OA于点E，如图2，线段PB与AD能否互相平分？若能，请求出点E的坐标；若不能，请说明理由．
参考答案：1．D【分析】根据三角形内心的性质解答即可．【详解】△ABC三个内角的平分线交于一点，且到三边的距离相等，所以探照灯的位置是三条角平分线的交点．故选：D．【点睛】本题主要考查了三角形内心的性质，即三角形的三个内角的平分线交于一点，且到三边的距离相等．2．C【分析】根据垂径定理可得：，DE=CE，进而得到∠COE=∠DOE，无法得到OE=BE．【详解】∵AB是⊙O的直径，CD为弦，CD⊥AB于点E，∴，DE=CE，，∴B，D选项正确；∵，∴，∴∠COE=∠DOE，∴A选项正确；只有当∠COE=60°时，才有OE=BE．∴C选项不成立；故选：C．【点睛】本题考查了垂径定理和圆心角、弧之间的关系．解题的关键是熟练掌握垂径定理．垂径定理：垂直弦的直径平分弦，并且平分弦所对的弧．3．B【分析】连接OA，根据切线性质得到∠OAB=90°，进而求得∠AOB=40°，再根据圆周角定理求得∠ADC，利用平行线性质即可求解∠OCD的度数．【详解】解：连接OA，如图，∵AB切⊙O于点A，∴OA⊥AB，∴∠OAB＝90°，∵∠B＝50°，∴∠AOB＝90°﹣50°＝40°，∴∠ADC∠AOB＝20°，∵，∴∠OCD＝∠ADC＝20°．故选：B．【点睛】本题考查切线性质、圆周角定理、平行线的性质、直角三角形的两锐角互余，熟练掌握切线的性质和圆周角定理是解答的关键．4．C【分析】根据圆的面积公式得出方程，根据算术平方根求出OA、OB、OC的值，再代入即可得出答案【详解】解：以OA半径的圆的面积是πr2，则以OB半径的圆的面积是πr2，则以OC半径的圆的面积是πr2∴πr2，πr2，∴OB＝r，OC＝r．∴OA：OB：OC＝r：r：r＝ ：：1，故选：C．【点睛】本题考查了正多边形与圆，算术平方根，圆的面积的应用，解此题的关键是能根据题意得出关于OA、OB、OC的方程，难度不是很大．5．C【分析】直接根据圆内接四边形的性质即可得出结论．【详解】解：∵四边形ABCD是⊙O的内接四边形，∴∠A+∠C=180°，∵∠A=60°，∴∠C=180°-60°=120°，故C正确．故选：C．【点睛】本题考查的是圆内接四边形的性质，熟知圆内接四边形的对角互补是解答此题的关键．6．C【分析】直接利用圆周角求解．【详解】解：∵点A是的中点，∴，∴∠AOB=2∠ADC=2×24°=48°．故选：C．【点睛】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．7．A【分析】根据题意得的半径为，则点到圆心的距离大于圆的半径，则根据点与圆的位置关系可判断点在内．【详解】解：的直径为10，的半径为5，而圆心的距离为6，点在外．故选：A．【点睛】本题考查了点与圆的位置关系，解题的关键是掌握设的半径为，点到圆心的距离，则有点在圆外；点在圆上；点在圆内．8．A【分析】连接，过点，分别作与，于，则四边形是矩形，证明，可得，根据垂径定理可得，根据即可求解．【详解】连接，过点，分别作于，于，则四边形是矩形，，，，，，（HL），，则，，，，．故选：A．【点睛】本题考查了垂径定理，掌握垂径定理是解题的关键．9．B【分析】连接OC，根据圆周角定理可得∠BOC=50°，∠DOC=60°，根据∠BOD=∠BOC+∠DOC即可求解．【详解】如图，连接OC，已知，，由圆周角定理可得∠BOC=50°，∠DOC=60°，所以∠BOD=∠BOC+∠DOC=50°+60°=110°．故选：D．【点睛】本题主要考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半，熟记定理是解题的关键．10．B【分析】直接利用等腰三角形的性质得出∠A的度数，再利用圆周角定理得出∠BOC的度数，再利用弧长公式求出答案．【详解】解：∵∠OCA＝50°，OA＝OC，∴∠A＝50°，∴∠BOC＝2∠A＝100°，∵AB＝4，∴BO＝2，∴的长为：π．故选：B．【点睛】此题主要考查了弧长公式应用以及圆周角定理，正确得出∠BOC的度数是解题关键．11．【分析】连接AB，根据90°的圆周角所对的弦是直径可知，AB是直径；再根据勾股定理求出OB的长，可得出答案．【详解】连接AB,∵∠AOB=90°，∴AB是直径，∴AB=10．又∵∠AOB=90°，点A的坐标为，∴，，∴，∴点的坐标为．故答案为：．【点睛】本题考查的定理是90°的圆周角所对的弦是直径，根据题意作出辅助线，构造出直角三角形，利用勾股定理求解是解答此题的关键．12．【分析】如图，连接BO，CO，OA．由题意得，△OBC，△AOB都是等边三角形，证明△OBC的面积=△ABC的面积， 可得图中阴影部分的面积等于扇形OBC的面积，再利用扇形的面积公式进行计算即可．【详解】解：如图，连接BO，CO，OA．由题意得，△OBC，△AOB都是等边三角形， ∴∠AOB=∠OBC=60°， ∴， ∴△OBC的面积=△ABC的面积， ∴图中阴影部分的面积等于扇形OBC的面积= ． 故答案为：【点睛】本题考查正多边形与圆、扇形的面积公式、平行线的性质等知识，解题的关键是学会用转化的扇形思考问题，属于中考常考题型．13．【分析】利用两个圆的面积减去一个正方形的面积求解即可．【详解】解：如图所示S阴影=-S正方形=-12=．故答案为：．【点睛】本题考查阴影面积的求解，利用S阴影=-S正方形进行求解是解决本题的关键．14．【分析】连接BE，BD，求出BE，BD，点E的运动轨迹是以B为圆心，2米为半径的弧，当点E落在线段BD上时，DE的值最小．【详解】解：如图，连接BE，BD，由题意（米），∵∠MBN=90°，MN=4米，EM=NE,∴BE= MN=2（米）,∴点E的运动轨迹是以B为圆心，2米为半径的弧，∴当点E落在线段BD上时，DE的值最小，∴DE的最小值为()米，（也可以用DE≥BD-BE，即DE≥确定最小值）．故答案为：．【点睛】本题考查点与圆的位置关系，直角三角形斜边中线的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．15．【分析】过点E作EF⊥BC垂足为F，如图，在Rt△DAB中，根据勾股定理可得AD的长，根据矩形和等边三角形性质可得AD=BC=BE=CE，根据勾股定理可计算出EF的长，根据代入计算即可得出答案．【详解】解：过点E作EF⊥BC垂足为F，如图，在Rt△DAB中，∴AD=BC=BE=CE=2，∵EF⊥BC，∴∴故答案为：．【点睛】本题主要考查了扇形面积的计算，熟练掌握扇形面积的计算方法进行求解是解决本题的关键．16．(1)见解析(2)2【分析】（1）连接OA，OE，OM，证明△AMO≌△AEO即可证明；（2）连接OF，证明四边形OFCE是正方形，在Rt△ABC中利用勾股定理解得AB，进而得到的半径．（1）证明：连接OA，OE，OM． AC切⊙O于点E，OE是⊙O的半径∴OE⊥AC∴∠AEO=90°                 在△AMO和△AEO中∴△AMO≌△AEO(SSS)   ∴∠AMO=∠AEO=90°     ∴OM⊥AB∵OM是⊙O的半径∴AB是⊙O的切线．（2）解：连接OF．设⊙O的半径为r．   ∵BC与⊙O相切于点F，∴OF⊥BC，∴∠OFC=90°，又因为∠C=90°，∠OEC=90°，且OF=OE，∴四边形OFCE是正方形， ∴CF=CE=OE=r，∵AB、BC、AC都与⊙O相切，∴BM=BF=6－r，AM=AE=8－r，在Rt△ABC中，，∵BM+AM=AB，∴6－r+8－r=10 ，∴   r=2        ∴⊙O的半径为2．【点睛】本题主要考查三角形全等的判定与性质，圆的切线的证明，勾股定理，掌握定理与性质是解题的关键．17．(1)，理由见解析(2)【分析】（1）根据直径所对的圆周角为直角，证明AD⊥BC，根据等腰三角形的性质，得出∠BAD＝∠DAE，即可得出答案；（2）连接OD，先证明，根据切线性质，得出OD⊥DF，得出DF⊥AC，根据勾股定理得出，根据等积法求出，根据勾股定理得出．（1）解：，理由如下：∵AB为⊙O直径，∴∠ADB＝90°，∴AD⊥BC，∵AB＝AC，∴∠BAD＝∠DAE，∴．（2）解：连接OD，如图所示：∵AD⊥BC，AB＝AC＝5，∴BD＝CD，∵AO＝BO，∴，∵DF是⊙O的切线，∴OD⊥DF，∴DF⊥AC，在Rt△ACD中，，∵S△ACDAD•CDAC•DF，∴，在Rt△ADF中，．【点睛】本题主要考查了圆周角定理，勾股定理，切线性质定理，等腰三角形的性质，平行线的性质，中位线的性质，三角形面积的计算，熟练掌握圆的有关性质，是解题的关键．18．(1)(2)【分析】（1）根据圆锥的母线、高和底面圆的半径构成直角三角形，利用勾股定理即可求解；（2）根据圆锥的底面圆周长是扇形的弧长，圆锥的母线长是扇形的半径进行计算即可．（1）解：如图，设为圆锥的高，为圆锥的母线，为底面圆的半径， ∴，，，∴有中，∴圆锥的高为．（2）圆锥的底面周长为：，∵圆锥的底面周长是侧面展开得到的扇形的弧长，∴扇形的弧长为，∴扇形的面积为，∴所需铁皮的面积为．【点睛】本题考查圆锥的计算．正确理解圆锥的高、母线与底面圆的半径构成直角三角形，圆锥的侧面与它的侧面展开图扇形之间的关系是解决本题的关键，要正确理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．19．(1)(2)8(3)线段PB与AD能互相平分，或【分析】（1）首先根据题意即可求得点A的坐标，再把两点的坐标分别代入解析式，解方程组即可求得；(2)设点P 则点D（t，-t），再由及二次函数的性质即可求得；(3)假设线段PB与AD能互相平分，再根据平行四边形的性质，即可求得．（1）解：∵过点A作AB⊥x轴，垂足为点B（－4，0），点A的横坐标为-4，点A的纵坐标为，点A的坐标为（－4，2），把点A（－4，2）、点（－2，5）分别代入解析式，得， 解得， ∴抛物线的解析式为；（2）解：设点P，AB=2，BO=4，，CO=-t，BC=4+t，∴ ， ，当t=-2时，S有最大值，最大值为8；（3）解：线段PB与AD能相互平分．如图：连接BD，设点P，则点D，则，假设线段PB与AD相互平分，则四边形ABDP是平行四边形，∴PD＝AB      即-t2-4t＝2，∴或当时，点E的横坐标为∴点E的坐标为，当时，点E的横坐标为，∴点E的坐标为 ∴点E的坐标为或，故当点E的坐标为或时，线段PB与AD互相平分．【点睛】本题考查了利用待定系数法求二次函数的解析式，求不规则图形的面积，二次函数的性质，坐标与图形，平行四边形的性质，采用反证法是解决本题的关键