高中数学人教A版 (2019)必修 第一册3.3 幂函数多媒体教学ppt课件

这是一份高中数学人教A版 (2019)必修 第一册3.3 幂函数多媒体教学ppt课件，文件包含§33幂函数pptx、§33幂函数docx等2份课件配套教学资源，其中PPT共60页， 欢迎下载使用。

§3.3　幂函数
第三章　函数的概念与性质
学习目标
1.掌握幂函数的概念、图象特征和性质.
2.掌握幂函数的图象位置和形状变化，会根据幂函数的单调性比较幂值的大小.
导语
同学们，我们说要想学好数学，就要先了解它的发展史，比如我们今天要学习的幂函数，“幂”其原意是遮盖东西用的布，后来引申为面积.《九章算术》刘徽注：“凡广纵相乘谓之幂.”后来又推广引申为多次乘方的结果.到了明清时代，既称面积为幂，也称平方或立方为幂.清末之后，幂逐渐开始专指乘方概念.
内容索引
幂函数的概念

一
问题1　下面几个实例，观察它们得出的函数解析式，有什么共同特征？(1)如果张红以1元/kg的价格购买了某种蔬菜ω kg，那么她需要支付p＝ω元，这里p是ω的函数；(2)如果正方形的边长为a，那么正方形的面积S＝a2，这里S是a的函数；(3)如果立方体的棱长为b，那么立方体的体积V＝b3，这里V是b的函数；(4)如果一个正方形场地的面积为S，那么这个正方形的边长c＝ ，这里c是S的函数；(5)如果某人t s内骑车行进了1 km，那么他骑车的平均速度v＝ km/s，即v＝t－1，这里v是t的函数.
提示　这些函数的解析式都具有幂的形式，而且都是以幂的底数为自变量，幂的指数都是常数.
知识梳理
幂函数的概念一般地，函数 叫做幂函数，其中x是 ，α是 .
y＝xα
常数
自变量
(1)自变量前的系数是1.(2)幂的系数为1.(3)α是任意常数.(4)函数的定义域与α有关.
注意点：
　　 (1)在函数y＝ ，y＝2x2，y＝x2＋x，y＝1中，幂函数的个数为A.0 　　B.1　　 C.2 　　 D.3
√
∵y＝ ＝x－2，∴是幂函数；y＝2x2由于出现系数2，因此不是幂函数；y＝x2＋x是两项和的形式，不是幂函数；y＝1＝x0(x≠0)，可以看出，常函数y＝1的图象比幂函数y＝x0的图象多了一个点(0,1)，所以常函数y＝1不是幂函数.
(2)已知y＝(m2＋2m－2) ＋2n－3是幂函数，求m，n的值.
幂函数的判断及应用(1)判断一个函数是否为幂函数的依据是该函数是否为y＝xα(α为常数)的形式，需满足：①指数为常数，②底数为自变量x，③自变量x前的系数为1.形如y＝(3x)α，y＝2xα，y＝xα＋5，…形式的函数都不是幂函数.(2)若一个函数为幂函数，则该函数也必具有y＝xα(α为常数)这一形式.
反思感悟
　　　 若函数f(x)是幂函数，且满足f(4)＝16，则f(－4)＝____.
设f(x)＝xα，∵f(4)＝16，∴4α＝16，解得α＝2，∴f(x)＝x2，∴f(－4)＝(－4)2＝16.
16
幂函数的图象与性质

二
问题2　根据之前所学，我们应该从哪些方面来研究幂函数？
提示　根据函数解析式先求出函数的定义域，然后画出函数图象，再利用图象和解析式研究函数的单调性、最值、值域、奇偶性、对称性等问题.
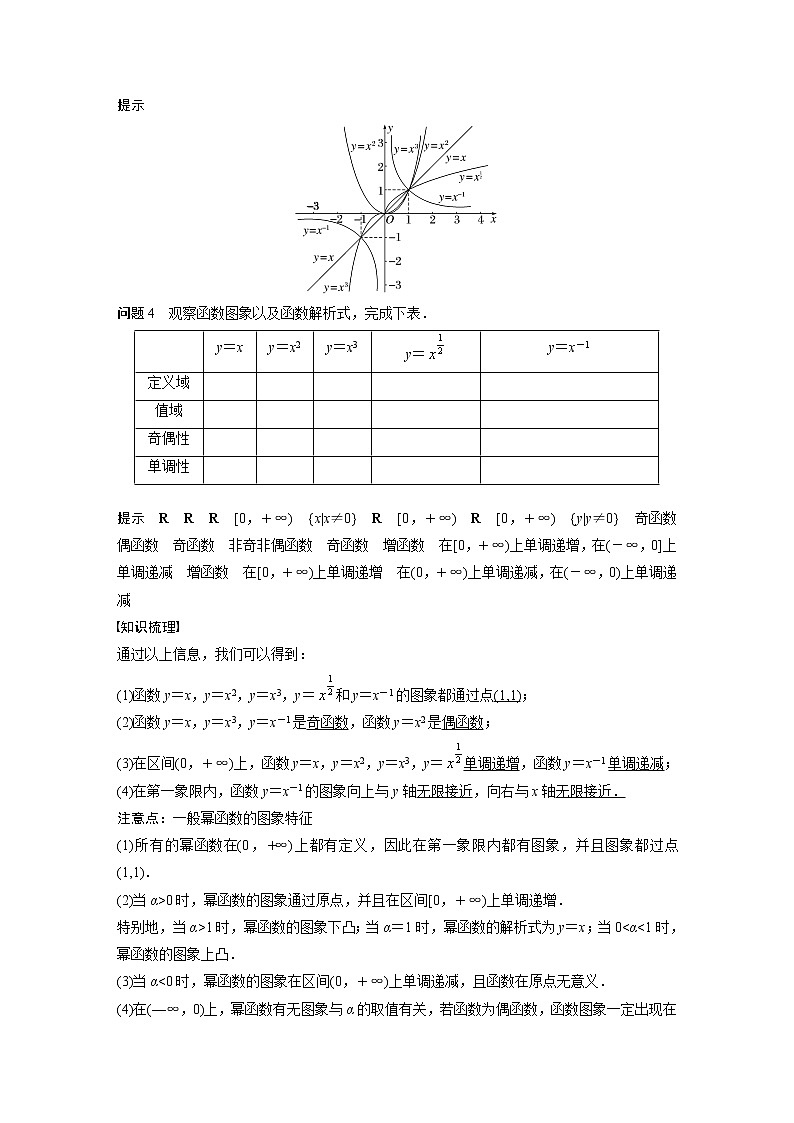
问题3　你能在同一坐标系下作出y＝x，y＝x2，y＝x3，y＝ ，y＝x－1这五个函数的图象吗？
提示　
问题4　观察函数图象以及函数解析式，完成下表.
R 　 R　 R　 [0，＋∞) {x|x≠0}
R　 [0，＋∞)　 R　 [0，＋∞)　 {y|y≠0}
奇函数　 偶函数 　 奇函数 非奇非偶函数　 奇函数
增函数
在[0，＋∞)上单调递增，在(－∞，0]上单调递减
增函数
在[0，＋∞)上单调递增
在(0，＋∞)上单调递减，在(－∞，0)上单调递减
知识梳理
通过以上信息，我们可以得到：(1)函数y＝x，y＝x2，y＝x3，y＝ 和y＝x－1的图象都通过点 ；(2)函数y＝x，y＝x3，y＝x－1是 ，函数y＝x2是 ；(3)在区间(0，＋∞)上，函数y＝x，y＝x2，y＝x3，y＝ ，函数y＝x－1 ；(4)在第一象限内，函数y＝x－1的图象向上与y轴 ，向右与x轴_________.
(1,1)
奇函数
偶函数
单调递增
单调递减
无限接近
无限接近
一般幂函数的图象特征(1)所有的幂函数在(0，＋∞)上都有定义，因此在第一象限内都有图象，并且图象都过点(1,1).(2)当α>0时，幂函数的图象通过原点，并且在区间[0，＋∞)上单调递增.特别地，当α>1时，幂函数的图象下凸；当α＝1时，幂函数的解析式为y＝x；当01).其中幂函数的个数为A.1 　　 B.2 　　 C.3 　　 D.4
√
②⑦为自变量在指数位置，③中系数不是1，④中解析式为多项式，⑤中底数不是自变量本身，所以只有①⑥是幂函数.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.若幂函数的图象过点(3，　)，则该幂函数的解析式是A.y＝x－1 B.y＝C.y＝x2 D.y＝x3
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3. 若四个幂函数y＝xa，y＝xb，y＝xc，y＝xd在同一坐标系中的图象如图，则a，b，c，d的大小关系是A.d>c>b>a B.a>b>c>dC.d>c>a>b D.a>b>d>c
√
在第一象限内，x＝1的右侧部分的图象，图象由下至上，幂指数由小到大，所以a>b>c>d.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.已知幂函数f(x)＝x4－m(m∈N*)为奇函数，且在区间(0，＋∞)上单调递增，则m等于A.1 　　B.2 　　C.1或3 　　 D.3
√
因为f(x)＝x4－m在(0，＋∞)上单调递增，所以4－m>0.所以m