高中数学人教A版 (2019)必修 第一册第一章 集合与常用逻辑用语1.3 集合的基本运算课文课件ppt

这是一份高中数学人教A版 (2019)必修 第一册第一章 集合与常用逻辑用语1.3 集合的基本运算课文课件ppt，文件包含§13第1课时集合的并集与交集运算pptx、§13第1课时集合的并集与交集运算docx等2份课件配套教学资源，其中PPT共57页， 欢迎下载使用。


第1课时　集合的并集与交集运算
第一章　§1.3　集合的基本运算
学习目标
1.理解两个集合的并集与交集的含义，会求两个简单集合的并集与交集.
2.能使用Venn图或数轴表达集合的关系及运算.
导语
在研究集合时，经常遇到有关集合中元素个数的问题，大家看一个问题，某超市进了两次货，第一次进的货是圆珠笔、钢笔、橡皮、笔记本、方便面、汽水共6种，第二次进的货是圆珠笔、铅笔、火腿肠、方便面共4种，两次一共进了几种货？两次进的货一样的有几种？我们说，数学的本身是解决实际问题，我们知道，实数有加、减、乘、除等运算，那么集合是否也有类似的运算呢？
内容索引
并集的运算

一
问题1　某超市进了两次货，第一次进的货是圆珠笔、钢笔、橡皮、笔记本、方便面、汽水共6种，第二次进的货是圆珠笔、铅笔、火腿肠、方便面共4种，我们用集合A表示第一次进货的品种，用集合B表示第二次进货的品种，通过观察，你能用集合C表示两次一共进货的品种吗？并讨论集合A，集合B与集合C的关系.
提示　A＝{圆珠笔，钢笔，橡皮，笔记本，方便面，汽水}，B＝{圆珠笔，铅笔，火腿肠，方便面}，则C＝{圆珠笔，钢笔，橡皮，笔记本，方便面，汽水，铅笔、火腿肠}，容易发现集合C是由所有属于集合A或属于集合B的元素组成的.
知识梳理
所有
并集
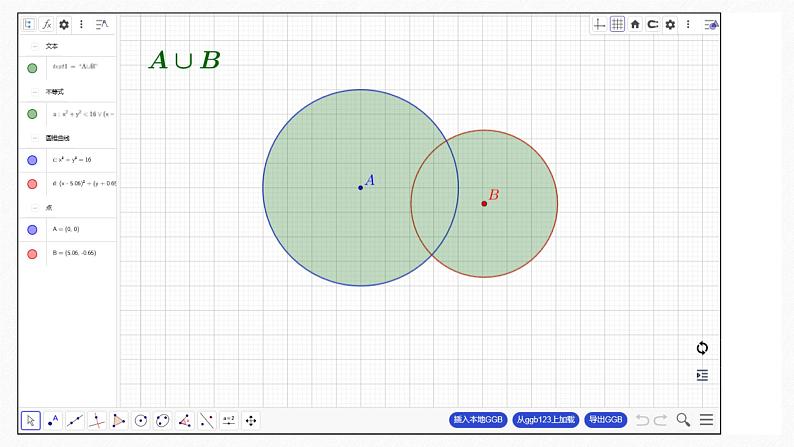
A∪B
A并B
{x|x∈A，或x∈B}
具体过程详见下页GeoGebra动画演示.
(1)A∪B仍是一个集合.(2)并集符号语言中的“或”包含三种情况：①x∈A且x∉B；②x∈A且x∈B；③x∉A且x∈B.(3)对概念中“所有”的理解，要注意集合元素的互异性.
注意点：
(1)设A＝{1,2,4,8}，B＝{1,4,9}，求A∪B.
A∪B＝{1,2,4,8}∪{1,4,9}＝{1,2,4,8,9}.
(2)设集合A＝{x|0≤x<4}，集合B＝{x|1≤x<5}，求A∪B.
A∪B＝{x|0≤x<4}∪{x|1≤x<5}＝{x|0≤x<5}.
并集的运算技巧(1)若集合中元素个数有限，则直接根据并集的定义求解，但要注意集合中元素的互异性.(2)若集合中元素个数无限，可借助数轴，利用数轴分析法求解，但要注意是否去掉端点值.
反思感悟
　设集合A＝{x|1≤x≤3}，B＝{x|2√
交集的运算

二
问题2　对于问题1中的集合A与集合B，你能用集合D表示两次进货一样的品种吗？并讨论集合A，B与集合D的关系.
提示　由A＝{圆珠笔，钢笔，橡皮，笔记本，方便面，汽水}，B＝{圆珠笔，铅笔，火腿肠，方便面}知，集合D＝{圆珠笔，方便面}，可见，集合D是由所有既属于集合A又属于集合B的元素组成的.
知识梳理
所有
交集
{x|x∈A，且x∈B}
具体过程详见下页GeoGebra动画演示.
(1)A∩B仍是一个集合.(2)文字语言中“所有”的含义：A∩B中任一元素都是A与B的公共元素，A与B的公共元素都属于A∩B.(3)如果两个集合没有公共元素，不能说两个集合没有交集，而是A∩B＝∅.
注意点：
　　(1)若集合A＝{x|－5√
M＝{x|－2≤x<2}，N＝{0,1,2}，则M∩N＝{0,1}.
(2)若集合M＝{x|－2≤x<2}，N＝{0,1,2}，则M∩N等于A.{0} B.{1}C.{0,1,2} D.{0,1}
√
交集运算的注意点(1)求集合交集的运算类似于并集的运算，其方法为①定义法，②数形结合法.(2)若A，B是无限连续的数集，多利用数轴来求解.但要注意，利用数轴表示不等式时，含有端点的值用实心点表示，不含有端点的值用空心圈表示.(3)注意点：若A⊆B，则A∩B＝A；若A＝B，则A∩B＝B＝A＝A∪B；A∩A＝A；A∩∅＝∅.
反思感悟
　　　(1)已知A＝{x|1{x|4借助数轴得A∩B＝{x|4(2)已知A＝{(x，y)|x＋y＝3}，B＝{(x，y)|x－y＝1}，则A∩B等于A.{2,1} B.{x＝2，y＝1}C.{(2,1)} D.(2,1)
√
根据并集与交集运算求参数范围

三
　　已知集合A＝{x|x≤－1或x≥3}，B＝{x|a利用数轴，若A∪B＝R，则a≤－1.
√
延伸探究　1.将例题中A∪B＝R变成A∪B＝A，求实数a的取值范围.
当a≥4时，集合B为空集，满足题意；当a<4时，若要满足A∪B＝A，必有a≥3.综上实数a的取值范围是a≥3.
2.例题中集合B变为B＝{x|a当a≥2时，集合B为空集，满足题意；当a<2时，则有a≥－1且4－a<3，故有11.
反思感悟
利用集合间的关系求参数范围的一般步骤为(1)若集合能一一列举，则用观察法得到不同集合中元素之间的关系；与不等式有关的集合，利用数轴得到不同集合间的关系.(2)将集合之间的关系转化为方程或不等式是否有解或解集的取值范围.(3)解方程(组)或不等式(组)，从而确定参数的值或取值范围.
　　　设集合M＝{x|－2{t|t≤2}
由M∩N＝N，得N⊆M.
故当N＝∅，即2t＋1≤2－t，即t≤ 时，M∩N＝N成立；
解得 课堂小结
1.知识清单：(1)并集的概念及运算.(2)交集的概念及运算.(3)根据集合间的运算求参数范围.2.方法归纳：观察法、图示法、数形结合、分类讨论.3.常见误区：在根据运算求参数范围时，容易遗忘空集这一重要的情况.
随堂演练

1.集合M＝{1,2,3,4,5}，集合N＝{1,3,5}，则A.N∈M B.M∪N＝MC.M∩N＝M D.M>N
√
因为NM，所以M∪N＝M.
1
2
3
4
1
2
3
4
2.若集合A＝{x|0√
∵A＝{x|03.满足{1,3}∪A＝{1,3,5}的所有集合A的个数是A.1 B.2 C.3 D.4
√
由{1,3}∪A＝{1,3,5}，知A⊆{1,3,5}且A中一定有元素5，因此集合A可以是{5}，{1,5}，{3,5}，{1,3,5}.
1
2
3
4
1
2
3
4
4.若集合A，B，C满足A∩B＝A，B∪C＝C，则A与C一定满足A.AC B.CAC.A⊆C D.C⊆A
√
A∩B＝A⇔A⊆B，B∪C＝C⇔B⊆C，所以A⊆C.
课时对点练

1.(多选)下列说法正确的有A.若x∈A，那么x∈A∩BB.若x∈A∩B，那么x∈AC.若x∈A∩B，那么x∈A∪BD.若x∈A，那么x∈A∪B
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
2.设集合A＝{x|－1≤x≤2}，B＝{x|0≤x≤4}，则A∩B等于A.{x|0≤x≤2} B.{x|－1≤x≤2}C.{x|0≤x≤4} D.{x|－1≤x≤4}
√
在数轴上表示出集合A与B，如图所示.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
则由交集的定义，知A∩B＝{x|0≤x≤2}.
3.设集合A＝{1,2,6}，B＝{2,4}，C＝{x|－1≤x≤5}，则(A∪B)∩C等于A.{2} B.{1,2,4}C.{1,2,4,6} D.{x∈R|－1≤x≤5}
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(A∪B)∩C＝{1,2,4,6}∩C＝{1,2,4}.
4.已知集合M＝{－1,1}，则满足M∪N＝{－1,1,2}的集合N的个数是A.1 B.2 C.3 D.4
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
依题意，得满足M∪N＝{－1,1,2}的集合N有{2}，{－1,2}，{1,2}，{－1,1,2}，共4个.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.设集合A＝{x|－1≤x<2}，B＝{x|x－2C.a>－1 D.－1√
在数轴上表示出集合A，B即可知a的取值范围是a＞－1.
6.(多选)若集合M⊆N，则下列结论正确的是A.M∩N＝M B.M∪N＝NC.N⊆(M∩N) D.(M∪N)⊆N
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.已知集合A＝ ，B＝{x∈Z|x≤2}，则A∩B＝_______.
{0,1,2}
M＝{x|－1≤x≤3}，集合N是全体正奇数组成的集合，则阴影部分所表示的集合为M∩N＝{1,3}，即阴影部分所表示的集合共有2个元素.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8. 已知集合M＝{x|－1≤x≤3}，N＝{x|x＝2k－1，k∈N*}，Venn图如图所示，则阴影部分所表示的集合的元素共有____个.
2
9.设A＝{x|x2＋ax＋12＝0}，B＝{x|x2＋3x＋2b＝0}，A∩B＝{2}，C＝{2，－3}.(1)求a，b的值及A，B；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵A∩B＝{2}，∴4＋2a＋12＝0,4＋6＋2b＝0，即a＝－8，b＝－5，∴A＝{x|x2－8x＋12＝0}＝{2,6}，B＝{x|x2＋3x－10＝0}＝{2，－5}.
∵A∪B＝{－5,2,6}，C＝{2，－3}，∴(A∪B)∩C＝{2}.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求(A∪B)∩C.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.已知集合A＝{x|－3≤x≤4}，B＝{x|2m－1＜x＜m＋1}.(1)若m＝－3，求A∩B；
m＝－3时，B＝{x|－7＜x＜－2}，故A∩B＝{x|－3≤x＜－2}.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若A∪B＝A，求实数m的取值范围.
因为A∪B＝A，故B⊆A，若2m－1≥m＋1，即m≥2，则B＝∅，符合题意；
综上，实数m的取值范围是m≥－1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.已知集合A＝{1,2}，B＝{x|mx－1＝0}，若A∩B＝B，则符合条件的实数m的值组成的集合为
√
12.(多选)已知集合A＝{4，a}，B＝{1，a2}，a∈R，则A∪B可能是A.{－1,1,4} B.{1,0,4}C.{1,2,4} D.{－2,1,4}
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.已知集合A＝{x|x2－px－2＝0}，B＝{x|x2＋qx＋r＝0}，且A∪B＝{－2,1,5}，A∩B＝{－2}，则p＋q＋r等于A.12　　　B.6 　　C.－14　　　D.－12
√
因为A∩B＝{－2}，所以－2∈A且－2∈B，将x＝－2代入x2－px－2＝0，得p＝－1，所以A＝{1，－2}，因为A∪B＝{－2,1,5}，A∩B＝{－2}，所以B＝{－2,5}，所以q＝－[(－2)＋5]＝－3，r＝(－2)×5＝－10，所以p＋q＋r＝－14.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.设集合M＝{x|－41
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
{t|t≤3}
由M∩N＝N，得N⊆M.故当N＝∅，即t＋2≥2t－1，即t≤3时，M∩N＝N成立；
综上可知，所求实数t的取值范围为{t|t≤3}.
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.某网店统计了连续三天售出商品的种类情况：第一天售出19种商品，第二天售出13种商品，第三天售出18种商品；前两天都售出的商品有3种，后两天都售出的商品有4种.则该网店(1)第一天售出但第二天未售出的商品有_____种；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设三天都售出的商品有x种，第一天售出，第二天未售出，且第三天售出的商品有y种，则三天售出商品的种类关系如图所示.由图可知，第一天售出但第二天未售出的商品有19－(3－x)－x＝16(种).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
这三天售出的商品有(16－y)＋y＋x＋(3－x)＋(6＋x)＋(4－x)＋(14－y)＝(43－y)种.
(2)这三天售出的商品最少有____种.
29
所以(43－y)min＝43－14＝29.
16.设集合A＝{2，－1，x2－x＋1}，B＝{2y，－4，x＋4}，C＝{－1,7}，且A∩B＝C，求实数x，y的值及A∪B.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
由题意，得7∈A，7∈B且－1∈B，所以在集合A中x2－x＋1＝7，解得x＝－2或x＝3.当x＝－2时，在集合B中，x＋4＝2，又2∈A，故2∈(A∩B)＝C，但2∉C，故x＝－2不符合题意，舍去.当x＝3时，在集合B中，x＋4＝7，
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以2y＝－1，解得y＝ ，符合题意，所以A＝{2，－1,7}，B＝{－1，－4,7}，所以A∪B＝{2，－1,7，－4}.