2023成都七中高三上学期入学考试数学（理）试卷含答案

这是一份2023成都七中高三上学期入学考试数学（理）试卷含答案，文件包含四川省成都七中2022-2023学年高三上学期入学考试数学理试卷无答案doc、四川省成都七中2022-2023学年高三上学期入学考试理科数学答案pdf等2份试卷配套教学资源，其中试卷共10页， 欢迎下载使用。
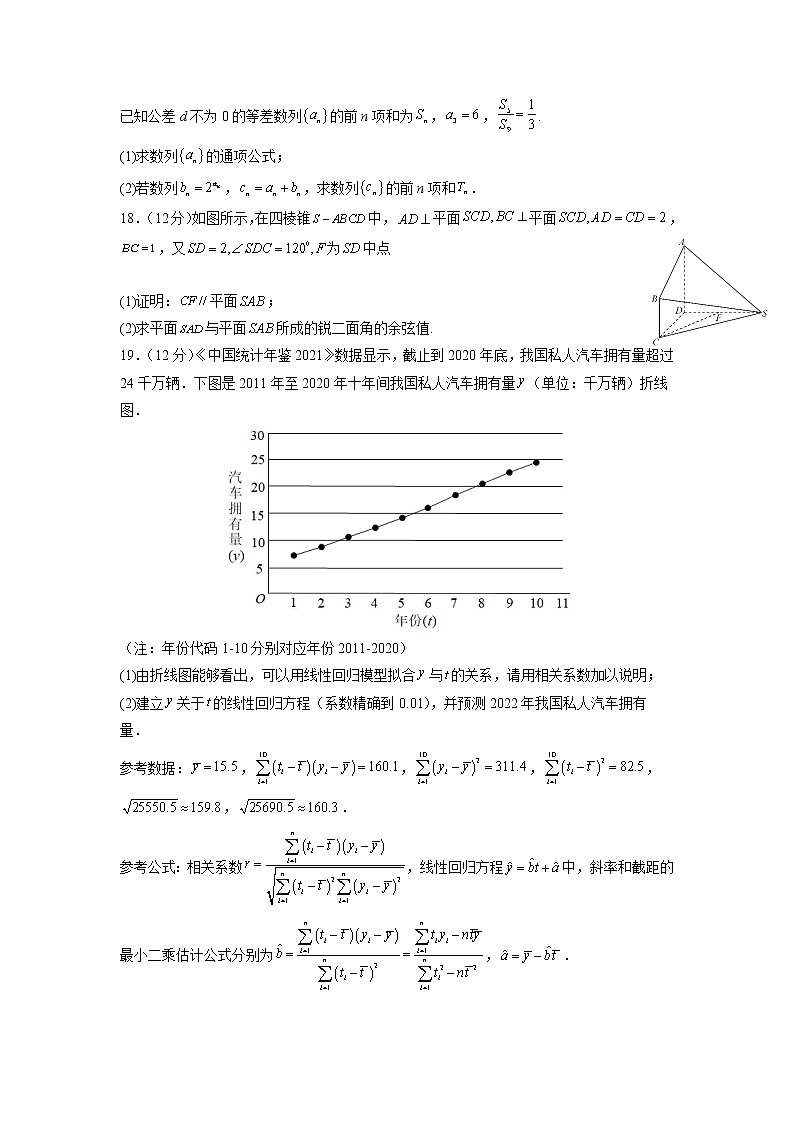
成都七中2023届高三上学期入学考试数学试卷（理科） 一、选择题（每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合要求的.）1．已知集合，，则（       ）A． B．C． D．2．设i为虚数单位，若复数是纯虚数，则实数（       ）A．－1 B．0 C．1 D．23．的展开式中含项的系数为（       ）A． B．24 C． D．4．已知，则外接圆的方程为（       ）A． B． C． D．5．已知一个半径为的扇形圆心角为，面积为，若，则（       ）A． B． C． D．6．考拉兹猜想是引人注目的数学难题之一，由德国数学家洛塔尔·考拉兹在世纪年代提出，其内容是：任意给定正整数，如果是奇数，则将其乘加；如果是偶数，则将其除以，所得的数再次重复上面步骤，最终都能够得到．下边的程序框图演示了考拉兹猜想的变换过程．若输入的值为，则输出的值为（       ） A． B． C． D．7．莫高窟坐落在甘肃的敦煌，它是世界上现存规模最大､内容最丰富的佛教艺术胜地，每年都会吸引来自世界各地的游客参观旅游.已知购买莫高窟正常参观套票可以参观8个开放洞窟，在这8个洞窟中莫高窟九层楼96号窟､莫高窟三层楼16号窟､藏经洞17号窟被誉为最值得参观的洞窟.根据疫情防控的需要，莫高窟改为极速参观模式，游客需从套票包含的开放洞窟中随机选择4个进行参观，所有选择中至少包含2个最值得参观洞窟的概率是（       ）A． B． C． D．8．设表示直线，表示平面，使“”成立的充分条件是（       ）A．， B．，C．， D．，，，9．等比数列的前n项和为，若，，则为（       ）A．1或9 B．1 C．9 D．310．设函数定义域为R，为奇函数，为偶函数，当时，，则下列结论错误的是（       ）A． B． 为奇函数C．在上为减函数 D．的一个周期为811．已知是椭圆：的左焦点，经过原点的直线与椭圆交于，两点，若，且，则椭圆的离心率为（       ）A． B． C． D．12．设，，，则的大小关系正确的是（       ）A． B． C． D．二、填空题：本大题共4小题，每小题5分，共20分.13．已知向量，，，则________.14．如图，一个正六棱柱的茶叶盒，底面边长为，高为，则这个茶叶盒的表面积约为______．15．在中，内角，，所对的边分别为，，，已知，若为的面积，则的最小值为______.16．已知抛物线的焦点为，过点做倾斜角为的动直线交于两点，过分别作的切线，，与交于点，，与轴的交点分别为，则四边形的面积为_______．三、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17．（12分）已知公差d不为0的等差数列的前n项和为，，.(1)求数列的通项公式；(2)若数列，，求数列的前n项和．18．（12分）如图所示，在四棱锥中，平面平面，，又为中点 (1)证明：平面；(2)求平面与平面所成的锐二面角的余弦值.19．（12分）《中国统计年鉴2021》数据显示，截止到2020年底，我国私人汽车拥有量超过24千万辆．下图是2011年至2020年十年间我国私人汽车拥有量（单位：千万辆）折线图．（注：年份代码1-10分别对应年份2011-2020）(1)由折线图能够看出，可以用线性回归模型拟合与的关系，请用相关系数加以说明；(2)建立关于的线性回归方程（系数精确到0.01），并预测2022年我国私人汽车拥有量．参考数据：，，，，，．参考公式：相关系数，线性回归方程中，斜率和截距的最小二乘估计公式分别为，．20．（12分）已知椭圆：的长轴长是短轴长的两倍，且过点.(1)求椭圆的方程.(2)设椭圆的下顶点为点，若不过点且不垂直于坐标轴的直线交椭圆于，两点，直线，分别与轴交于，两点.若，的横坐标之积是2，证明：直线过定点.21．（12分）已知函数.（1）已知恒成立，求的值；（2）证明：当时，；（3）当时，不等式，求的取值范围.22．（10分）在平面直角坐标系xOy中，设曲线的参数方程为（t为参数），以坐标原点O为极点，以x轴正半轴为极轴建立极坐标系，设曲线的极坐标方程为．(1)求曲线的普通方程；(2)若曲线上恰有三个点到曲线的距离为，求实数a的值．