浙教版八年级下册4.4 平行四边形的判定课堂教学ppt课件

这是一份浙教版八年级下册4.4 平行四边形的判定课堂教学ppt课件，共21页。PPT课件主要包含了平行四边形的定义，平行四边形的性质，平行四边形的对边平行，平行四边形的对边相等，平行四边形的对角相等，平行四边形的邻角互补等内容，欢迎下载使用。
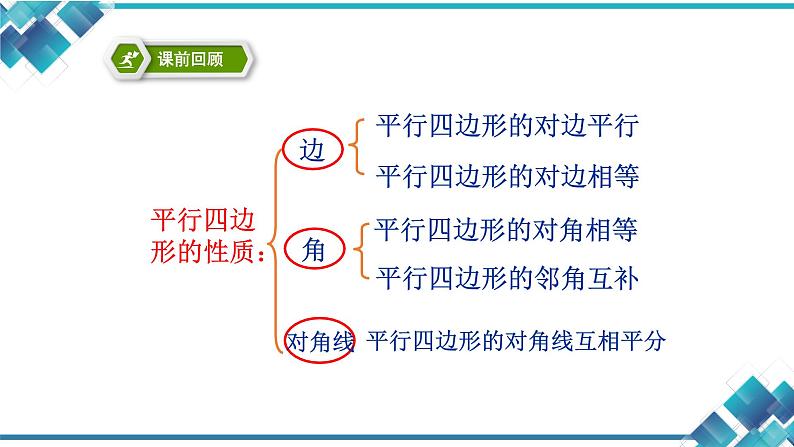
两组对边分别平行的四边形叫做平行四边形。
平行四边形的对角线互相平分
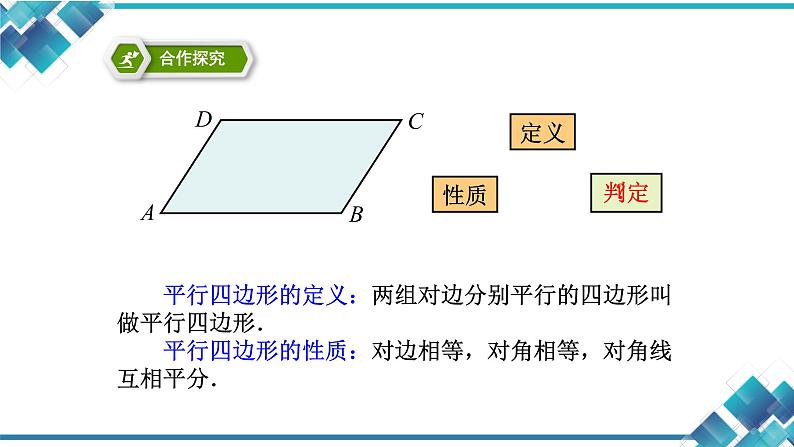
　　平行四边形的定义：两组对边分别平行的四边形叫做平行四边形．　　平行四边形的性质：对边相等，对角相等，对角线互相平分．
如何寻找平行四边形的判定方法？
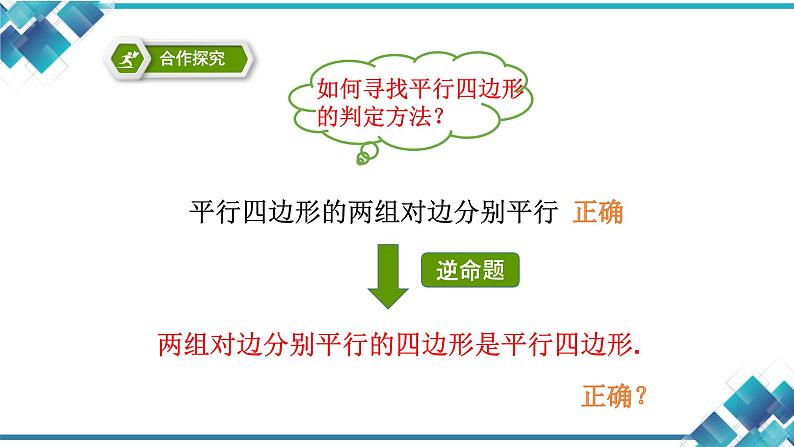
平行四边形的两组对边分别平行
两组对边分别平行的四边形是平行四边形.
　　 　 两组对边分别平行的四边形是平行四边形．　　
根据平行四边形的定义：两组对边分别平行的四边形叫做平行四边形．我们可以得到我们的猜想正确。
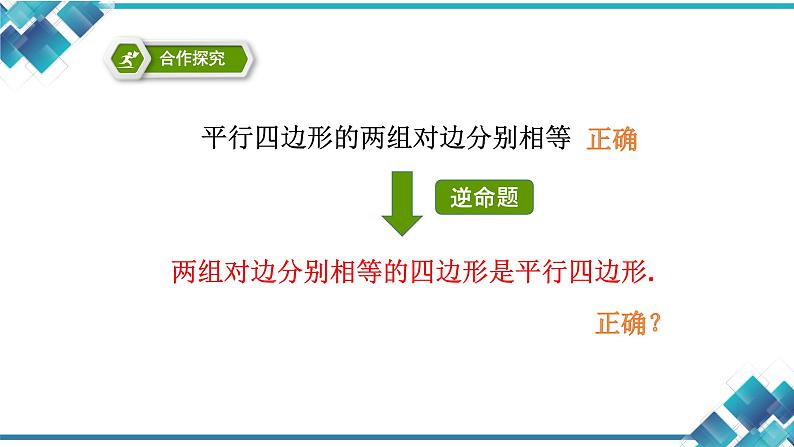
平行四边形的两组对边分别相等
两组对边分别相等的四边形是平行四边形.
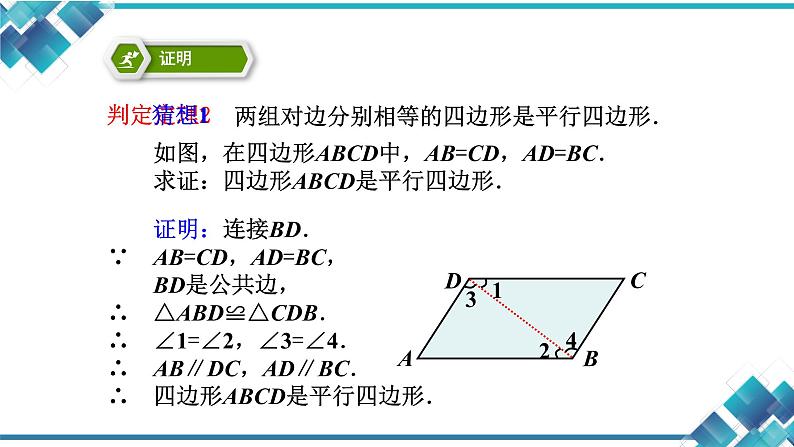
　　证明：连接BD．∵　AB=CD，AD=BC， BD是公共边，∴　△ABD≌△CDB．∴　∠1=∠2，∠3=∠4．∴　AB∥DC，AD∥BC．∴　四边形ABCD是平行四边形．
　　如图，在四边形ABCD中，AB=CD，AD=BC．　　求证：四边形ABCD是平行四边形．
　　 　 两组对边分别相等的四边形是平行四边形．　　
如果仅仅是一组对边平行且相等呢？
一组对边平行且相等的四边形是平行四边形
已知：在四边形ABCD中，AD＝BC，AD∥BC。求证：四边形ABCD是平行四边形。
试一试证明我们的猜想是否正确。
证明:如图,连结BD.∵AD∥BC∴∠ADB=∠CBD（两直线平行，内错角相等）又∵AD=BC,BD=BD∴△ADB≌△CBD (SAS)∴∠ABD=∠CDB（全等三角形的对应角相等）∴AB∥DC（内错角相等，两直线平行）∴四边形ABCD是平行四边形（两组对边分别平行的四边形是平行四边形）
平行四边形判定定理3：
一组对边平行且相等的四边形是平行四边形。
两组对边分别平行的四边形是平行四边形。
平行四边形判定定理1：
∵ AB//CD且AD//BC
∴四边形ABCD是平行四边形
我们总共学了几个平行四边形的判定方法呢？
两组对边分别相等的四边形是平行四边形。
平行四边形判定定理2：
∵ AB=CD且AD=BC
∵ AB∥CD且AB=CD
猜想4：一组对边平行，另一组对边相等的四边形是平行四边形吗？
等腰梯形的一组对边平行，另一组对边相等，猜想不正确
例1：已知，如图，在□ABCD中，点E、F分别是边AB、CD的中点. 求证：EF//AD
提示：一组对边平行且相等的四边形是平行四边形.
∵四边形ABCD是平行四边形∴AB∥CD且AB=CD∵点E、F分别是边AB、CD的中点∴AE∥DF 且AE=DF∴ 四边形AEFD是平行四边形∴ AD∥EF
已知，四边形ABCD和AEFD都是平行四边形求证：四边形BCFE是平行四边形
证明：∵四边形ABCD是平行四边形 ∴AD∥BC且 AD=BC ； 同理AD∥EF且AD=EF ∴ BC∥EF且BC=EF ∴四边形BCFE是平行四边形
已知直角坐标系内四个点A（a，1），B（b，1），C（c，-1）D（d，-1）。四边形ABCD一定是平行四边形吗？如果你认为是，请给出证明；如果你认为不一定是，请添加一个条件，使他一定是平行四边形。
的四边形是平行四边形
这节课我们学到了什么？