








所属成套资源:【最新版】 新教材人教A版选择性必修一【学案+同步课件】
2020-2021学年2.4 圆的方程说课ppt课件
展开
这是一份2020-2021学年2.4 圆的方程说课ppt课件,文件包含251第2课时直线与圆的方程的实际应用pptx、251第2课时直线与圆的方程的实际应用docx等2份课件配套教学资源,其中PPT共60页, 欢迎下载使用。
1.理解并掌握直线与圆的方程在实际生活中的应用.
2.会用“数形结合”的数学思想解决问题.
当前台风中心P在某海滨城市O向东300 km处生成,并以40 km/h的速度向西偏北45°方向移动.已知距离台风中心250 km以内的地方都属于台风侵袭的范围,那么经过多长时间后该城市开始受到台风侵袭?受台风侵袭大概持续多长时间?
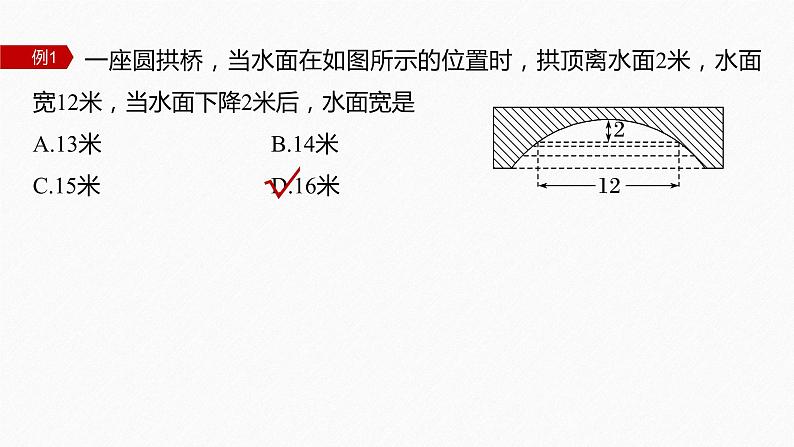
一座圆拱桥,当水面在如图所示的位置时,拱顶离水面2米,水面宽12米,当水面下降2米后,水面宽是A.13米 B.14米 C.15米 D.16米
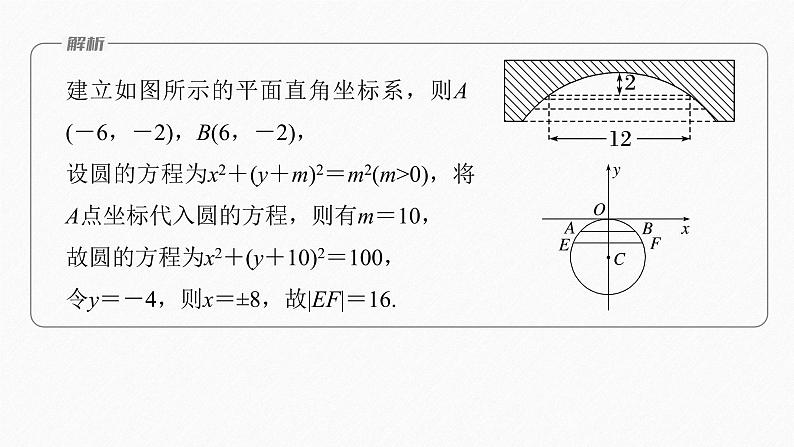
建立如图所示的平面直角坐标系,则A(-6,-2),B(6,-2),设圆的方程为x2+(y+m)2=m2(m>0),将A点坐标代入圆的方程,则有m=10,故圆的方程为x2+(y+10)2=100,令y=-4,则x=±8,故|EF|=16.
建立适当的直角坐标系,用坐标和方程表示问题中的几何要素,通过代数运算,解决几何问题.
一辆平顶车篷的卡车宽2.7米,要经过一个半径为4.5米的半圆形隧道(双车道,不得违章),则这辆卡车的篷顶距离地面的高度不得超过A.1.4米 B.3.0米C.3.6米 D.4.5米
直线与圆的方程的实际应用
如图,某海面上有O,A,B三个小岛(面积大小忽略不计),A岛在O岛的北偏东45°方向距O岛 千米处,B岛在O岛的正东方向距O岛20千米处.以O为坐标原点,O的正东方向为x轴的正方向,1千米为单位长度,建立平面直角坐标系.圆C经过O,A,B三点.(1)求圆C的方程;
由题意,得A(40,40),B(20,0),设过O,A,B三点的圆C的方程为x2+y2+Dx+Ey+F=0,
∴圆C的方程为x2+y2-20x-60y=0.
(2)若圆C区域内有未知暗礁,现有一船D在O岛的南偏西30°方向距O岛40千米处,正沿着北偏东45°方向行驶,若不改变方向,试问该船有没有触礁的危险?
且该船航线所在直线l的斜率为1,
解决直线与圆的实际应用题的步骤(1)审题:从题目中抽象出几何模型,明确已知和未知.(2)建系:建立适当的直角坐标系,用坐标和方程表示几何模型中的基本元素.(3)求解:利用直线与圆的有关知识求出未知.(4)还原:将运算结果还原到实际问题中去.
如图是某主题公园的部分景观平面示意图,圆形池塘以O为圆心,以 m为半径,B为公园入口,道路AB为东西方向,道路AC经过点O且向正北方向延伸,OA=10 m,AB=100 m,现计划从B处起修一条新路与道路AC相连,且新路在池塘的外围,假设路宽忽略不计,则新路的最小长度为(单位:m)
1.知识清单: (1)直线与圆的方程的应用. (2)坐标法的应用.2.方法归纳:数学建模、坐标法.3.常见误区:不能正确进行数学建模.
1.一涵洞的横截面是半径为5 m的半圆,则该半圆的方程是A.x2+y2=25B.x2+y2=25(y≥0)C.(x+5)2+y2=25(y≤0) D.随建立直角坐标系的变化而变化
2.y=|x|的图象和圆x2+y2=4在x轴上方所围成的图形的面积是
3.设某村庄外围成圆形,其所在曲线的方程可用(x-2)2+(y+3)2=4表示,村外一小路方程可用x-y+2=0表示,则从村庄外围到小路的最短距离是________.
从村庄外围到小路的最短距离为圆心(2,-3)到直线x-y+2=0的距离减去圆的半径2,
4.一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西70 km处,受影响的范围是半径长为30 km的圆形区域.已知港口位于台风中心正北40 km处,如果这艘轮船不改变航线,那么它________(填“会”“不会”)受到台风的影响.
如图,以台风中心为原点O,以东西方向为x轴,建立直角坐标系,其中,取10 km为单位长度.则台风影响的圆形区域所对应的圆心为O,圆的方程为x2+y2=9;轮船航线所在的直线l的方程为4x+7y-28=0.可知直线与圆相离,故轮船不会受到台风的影响.
1.如图,圆弧形拱桥的跨度|AB|=12米,拱高|CD|=4米,则拱桥的直径为A.15米 B.13米C.9米 D.6.5米
如图,设圆心为O,半径为r,则由勾股定理得|OB|2=|D|2+|BD|2,即r2=(r-4)2+62,
所以拱桥的直径为13米.
2.已知点A(-1,1)和圆C:(x-5)2+(y-7)2=4,一束光线从点A经x轴反射到圆C上的最短路程是
点A关于x轴的对称点A′(-1,-1),A′与圆心(5,7)的距离为 =10.∴所求最短路程为10-2=8.
3.一辆货车宽1.6米,要经过一个半径为3.6米的半圆形单行隧道,则这辆货车的平顶车篷的篷顶距离地面高度最高约为A.2.4米 B.3.5米 C.3.6米 D.2.0米
以半圆所在直径为x轴,过圆心且与x轴垂直的直线为y轴,建立如图所示的平面直角坐标系.易知半圆所在的圆的方程为x2+y2=3.62(y≥0),由图可知,当货车恰好在隧道中间行走时车篷最高,此时x=0.8或x=-0.8,代入x2+y2=3.62,得y≈3.5(负值舍去).
4.为了适应市场需要,某地准备建一个圆形生猪储备基地(如图),它的附近有一条公路,从基地中心O处向东走1 km是储备基地的边界上的点A,接着向东再走7 km到达公路上的点B;从基地中心O向正北走8 km到达公路的另一点C.现准备在储备基地的边界上选一点D,修建一条由D通往公路BC的专用线DE,则DE的最短距离为
以O为坐标原点,过OB,OC的直线分别为x轴和y轴,建立平面直角坐标系(图略),则圆O的方程为x2+y2=1,因为点B(8,0),C(0,8),
5.设某公园外围成圆形,其所在曲线的方程可用x2+y2-2x=0表示,在公园外两点A(-2,0),B(0,2)与公园边上任意一点修建一处舞台,则舞台面积的最小值为
6.(多选)从点A(-3,3)发出的光线l射到x轴上被x轴反射后,照射到圆C:x2+y2-4x-4y+7=0上,则下列结论正确的是
即4x-3y+3=0或3x-4y-3=0,故A错误;又A′(-3,-3),C(2,2)的方程为y=x,故B正确;
7.某圆弧形拱桥的水面跨度是20 m,拱高为4 m.现有一船宽9 m,在水面以上部分高3 m,通行无阻.近日水位暴涨了1.5 m,为此,必须加重船载,降低船身,当船身至少降低________m时,船才能安全通过桥洞.(结果精确到0.01 m)
以水位未涨前的水面AB的中点O为原点,建立平面直角坐标系,如图所示,设圆拱所在圆的方程为x2+(y-b)2=r2(0≤y≤4),∵圆经过点B(10,0),C(0,4),
∴圆的方程是x2+(y+10.5)2=14.52(0≤y≤4),
令x=4.5,得y≈3.28,故当水位暴涨1.5 m后,船身至少应降低1.5-(3.28-3)=1.22(m),船才能安全通过桥洞.
8.台风中心从A地以20 km/h的速度向东北方向移动,离台风中心30 km内的地区为危险区,城市B在A地正东40 km处,则城市B处于危险区的时间为____h.
如图,以A地为坐标原点,AB所在直线为x轴,建立平面直角坐标系,则台风中心经过以B(40,0)为圆心,30为半径的圆内时城市B处于危险区,
所以城市B处于危险区的时间为1 h.
9.设有半径长为3 km的圆形村落,甲、乙两人同时从村落中心出发,甲向东前进而乙向北前进,甲离开村后不久,改变前进方向,斜着沿切于村落边界的方向前进,后来恰好与乙相遇.设甲、乙两人的速度都一定,且其速度比为3∶1,问:甲、乙两人在何处相遇?
如图所示,以村落中心为坐标原点,以东西方向为x轴,南北方向为y轴建立平面直角坐标系.
所以乙向北前进3.75 km时甲、乙两人相遇.
10.如图,已知一艘海监船O上配有雷达,其监测范围是半径为25 km的圆形区域,一艘外籍轮船从位于海监船正东40 km的A处出发,径直驶向位于海监船正北30 km的B处岛屿,速度为28 km/h.问:这艘外籍轮船能否被海监船监测到?若能,持续时间多长?(要求用坐标法)
如图,以O为坐标原点,东西方向为x轴建立平面直角坐标系,则A(40,0),B(0,30),圆O的方程为x2+y2=252.
即3x+4y-120=0.设点O到直线AB的距离为d,
所以外籍轮船能被海监船监测到.设监测时间为t,
11.(多选)如图所示,已知直线l的方程是y= x-4,并且与x轴、y轴分别交于A,B两点,一个半径为1.5的圆C,圆心C从点(0,1.5)开始以每秒0.5个单位的速度沿着y轴向下运动,当圆C与直线l相切时,该圆运动的时间可以为A.6秒 B.8秒 C.10秒 D.16秒
设当圆与直线l相切时,圆心坐标为(0,m),
12.某圆拱桥的示意图如图所示,该圆拱的跨度AB是36 m,拱高OP是6 m,在建造时,每隔3 m需用一个支柱支撑,则支柱A2P2的长为
如图,以线段AB所在的直线为x轴,线段AB的中点O为坐标原点建立平面直角坐标系,那么点A,B,P的坐标分别为(-18,0),(18,0),(0,6).设圆拱所在的圆的方程是x2+y2+Dx+Ey+F=0.因为A,B,P在此圆上,故有
故圆拱所在圆的方程是x2+y2+48y-324=0.
将点P2的横坐标x=6代入上式,
13.如图,正方形ABCD的边长为20米,圆O的半径为1米,圆心是正方形的中心,点P,Q分别在线段AD,CB上,若线段PQ与圆O有公共点,则称点Q在点P的“盲区”中,已知点P以1.5米/秒的速度从A出发向D移动,同时,点Q以1米/秒的速度从C出发向B移动,则在点P从A移动到D的过程中,点Q在点P的盲区中的时长约________秒(精确到0.1).
以点O为坐标原点,建立如图所示的平面直角坐标系,
可设点P(-10,-10+1.5t),Q(10,10-t),可得出直线PQ的方程y-10+t= (x-10),圆O的方程为x2+y2=1,
因此,点Q在点P的盲区中的时长约为4.4秒.
14.如图是一公路隧道截面图,下方ABCD是矩形,且AB=4 m,BC=8 m,隧道顶APD是一圆弧,拱高OP=2 m,隧道有两车道EF和FG,每车道宽3.5 m,车道两边留有0.5 m的人行道BE和GC,为了行驶安全,车顶与隧道顶端至少有0.6 m的间隙,则此隧道允许通行车辆的限高是______m.(精确到0.01 m, ≈7.141)
建立如图所示的平面直角坐标系Oxy,设弧APD所在圆的圆心坐标为O1(0,b),半径为r,则其方程为x2+(y-b)2=r2.将P(0,2),D(4,0)的坐标代入以上方程,解得b=-3,r=5,故圆O1的方程为x2+(y+3)2=25.
则|EN|=4+0.570 5=4.570 5,从而车辆的限高为4.570 5-0.6≈3.97(m).
方法一 以A为原点,AD所在直线为x轴建立平面直角坐标系,如图,
则直线AB的方程为4x+3y=0,直线CD的方程为3x-4y-105=0,直线EF的方程为y=12,
设圆心为O(a,b),则圆心到直线AB,直线CD,直线y=12的距离均相等且等于r,
解得a=15,b=0,r=12,
16.如图所示,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80 m.经测量,点A位于点O正北方向60 m处,点C位于点O正东方向170 m处(OC为河岸),tan∠BCO= .(1)求新桥BC的长;
如图,以O为坐标原点,OC所在直线为x轴建立平面直角坐标系Oxy.由条件知,A(0,60),C(170,0),
设点B的坐标为(a,b),
联立①②解得a=80,b=120.
因此新桥BC的长为150 m.
(2)当OM为多长时,圆形保护区的面积最大?
设保护区的边界圆M的半径为r m,|OM|=d m(0≤d≤60).
即4x+3y-680=0.由于圆M与直线BC相切,故点M(0,d)到直线BC的距离是r,
因为O和A到圆M上任意一点的距离均不少于80 m,
相关课件
这是一份高中数学2.5 直线与圆、圆与圆的位置课前预习ppt课件,文件包含251第1课时直线与圆的位置关系pptx、251第1课时直线与圆的位置关系docx等2份课件配套教学资源,其中PPT共53页, 欢迎下载使用。
这是一份数学选择性必修 第一册2.3 直线的交点坐标与距离公式教学课件ppt,文件包含233点到直线的距离公式234两条平行直线间的距离pptx、233点到直线的距离公式docx等2份课件配套教学资源,其中PPT共43页, 欢迎下载使用。
这是一份人教A版 (2019)选择性必修 第一册3.2 双曲线教学课件ppt,文件包含322第2课时双曲线的标准方程及性质的应用pptx、322第2课时双曲线的标准方程及性质的应用docx等2份课件配套教学资源,其中PPT共60页, 欢迎下载使用。









