高中数学人教A版 (2019)选择性必修 第一册1.4 空间向量的应用图片ppt课件

这是一份高中数学人教A版 (2019)选择性必修 第一册1.4 空间向量的应用图片ppt课件，文件包含112空间向量的数量积运算pptx、112空间向量的数量积运算docx等2份课件配套教学资源，其中PPT共60页， 欢迎下载使用。
1.了解空间向量的夹角.
2.掌握空间向量的数量积的定义、性质、运算律及计算方法.
3.了解空间向量投影的概念以及投影向量的意义.
4.掌握两个向量的数量积在判断垂直中的应用，掌握利用向量数量积求空间两点间的距离.
在平面向量中已经学过两个平面向量的数量积运算，由于任意两个空间向量都可以通过平移转化为同一平面内的向量，因此，两个空间向量的夹角和数量积就可以像平面向量那样来定义.
(1)对于空间任意两个非零向量a，b，“a∥b”是“〈a，b〉＝0”的A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件
显然〈a，b〉＝0⇒a∥b，但a∥b包括向量a，b同向共线和反向共线两种情况，即当a∥b时，〈a，b〉＝0或π，因此a∥b⇏〈a，b〉＝0.故“a∥b”是“〈a，b〉＝0”的必要不充分条件.
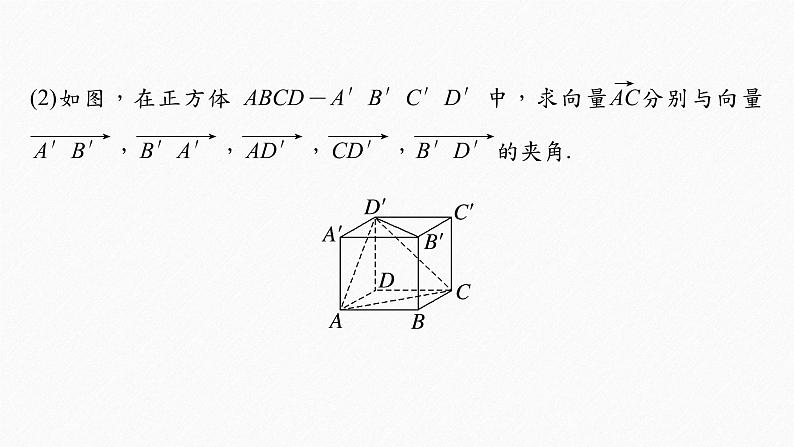
连接BD(图略)，则在正方体ABCD－A′B′C′D′中，AC⊥BD，∠BAC＝45°，AC＝AD′＝CD′，
(1)只有两个非零空间向量才有夹角，当两个非零空间向量共线同向时，夹角为0，共线反向时，夹角为π.(2)对空间任意两个非零向量a，b有：①〈a，b〉＝〈b，a〉；②〈－a，b〉＝〈a，－b〉＝π－〈a，b〉；③〈－a，－b〉＝〈a，b〉.
在正四面体ABCD中， 的夹角等于A.30° B.60° C.150° D.120°
1.(1)空间向量的数量积已知两个非零向量a，b，则|a||b|cs〈a，b〉叫做a，b的数量积，记作a·b，即a·b＝ .零向量与任意向量的数量积为0，即0·a＝ .(2)运算律
|a||b|·cs〈a，b〉
2.向量的投影(1)如图①，在空间，向量a向向量b投影，由于它们是自由向量，因此可以先将它们平移到同一个平面α内，进而利用平面上向量的投影，得到与向量b共线的向量c，c＝|a|cs〈a，b〉 ，向量c称为向量a在向量b上的投影向量.类似地，可以将向量a向直线l投影(如图②).
(1)向量a，b的数量积记为a·b，而不能表示为a×b或者ab.(2)向量的数量积的结果为实数，而不是向量，它可以是正数、负数或零，其符号由夹角θ的范围决定.①当θ为锐角时，a·b>0；但当a·b>0时，θ不一定为锐角，因为θ也可能为0.②当θ为钝角时，a·b