高中数学人教B版 (2019)必修 第二册4.1.2 指数函数的性质与图像第1课时学案

这是一份高中数学人教B版 (2019)必修 第二册4.1.2 指数函数的性质与图像第1课时学案，共13页。学案主要包含了指数函数的概念，简单指数函数的图像，简单指数型函数的性质等内容，欢迎下载使用。
学习目标 1.理解指数函数的概念，了解底数的限制条件的合理性.2.掌握指数函数图像的性质.3.会应用指数函数的性质求复合函数的定义域、值域．
导语
古希腊著名数学家阿基米德与国王下棋．国王输了，问阿基米德要什么奖赏？阿基米德说：“我只要在棋盘上的第一格放一粒米，第二格放二粒，第三格放四粒，第四格放八粒…….按此方法放到第64个格子就行了．” 国王一听，随即答应了．但是所有64个方格上的颗粒总数为1＋2＋4＋8＋…＋263，经过计算约为18.447亿吨大米！国王如何赏得起？今天我们就从这个关于数学指数增长的故事开始今天的学习吧！
一、指数函数的概念
问题1 用列表、描点、连线的画图步骤，先完成下列表格，再画出指数函数y＝2x与y＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))x的图像.
提示 (1)eq \f(1,4) eq \f(1,2) 1 2 4 4 2 1 eq \f(1,2) eq \f(1,4)
(2)y＝2x和y＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))x的图像如图所示．
知识梳理
指数函数的定义
一般地，函数y＝ax称为指数函数，其中a是常数，a>0且a≠1.
注意点：
(1)系数为1.
(2)底数为常数a.
(3)自变量x为指数．
例1 (1)(多选)下列一定是指数函数的是( )
A．y＝ax(a>0且a≠1)
B．y＝xa(a>0且a≠1)
C．y＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))x
D．y＝(a－2)ax
(2)已知指数函数y＝(2b－3)ax经过点(1,2)，则a＝________，b＝________.
答案 (1)AC (2)2 2
解析 (1)A中a的范围正确，故是指数函数；
B中y＝xa(a>0且a≠1)中底数是变量，故不是指数函数；
C中y＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))x显然是指数函数；
D中只有a－2＝1，即a＝3时为指数函数．
(2)由指数函数定义可知2b－3＝1，即b＝2.将点(1,2)代入y＝ax，得a＝2.
反思感悟 判断一个函数是否为指数函数的方法
(1)底数的值是否符合要求．
(2)ax前的系数是否为1.
(3)指数是否符合要求．
跟踪训练1 (1)若函数y＝a2(2－a)x是指数函数，则( )
A．a＝1或－1 B．a＝1
C．a＝－1 D．a>0且a≠1
(2)已知函数f(x)是指数函数，且f eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(3,2)))＝eq \f(\r(5),25)，则f(3)＝________.
答案 (1)C (2)125
解析 (1)因为函数y＝a2(2－a)x是指数函数，
所以eq \b\lc\{\rc\ (\a\vs4\al\c1(a2＝1，,2－a>0，,2－a≠1，))即a＝－1.
(2)设f(x)＝ax(a>0且a≠1)，由f eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(3,2)))＝eq \f(\r(5),25)得，
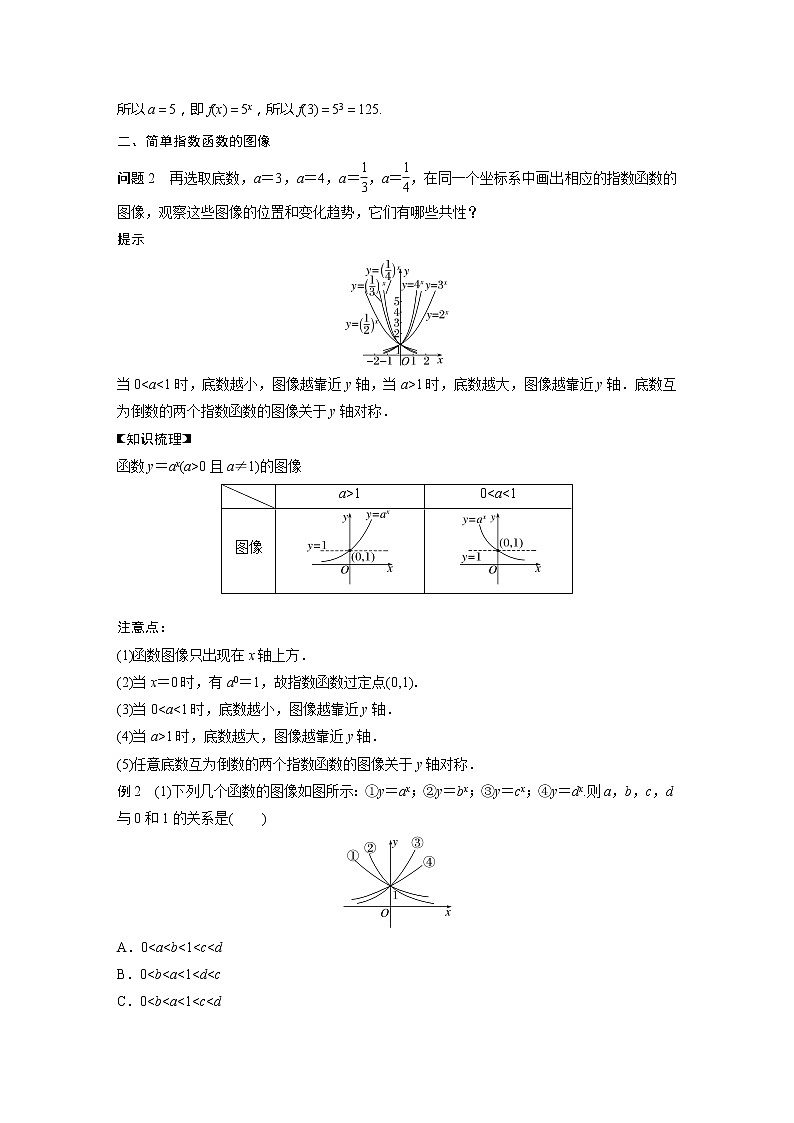
所以a＝5，即f(x)＝5x，所以f(3)＝53＝125.
二、简单指数函数的图像
问题2 再选取底数，a＝3，a＝4，a＝eq \f(1,3)，a＝eq \f(1,4)，在同一个坐标系中画出相应的指数函数的图像，观察这些图像的位置和变化趋势，它们有哪些共性？
提示
当00且a≠1)的图像
注意点：
(1)函数图像只出现在x轴上方．
(2)当x＝0时，有a0＝1，故指数函数过定点(0,1)．
(3)当0