人教B版 (2019)必修 第二册5.1.3 数据的直观表示备课课件ppt

这是一份人教B版 (2019)必修 第二册5.1.3 数据的直观表示备课课件ppt，共60页。PPT课件主要包含了柱形图与折线图，扇形图，茎叶图，随堂演练，课时对点练等内容，欢迎下载使用。
1.了解统计图表的作用与意义.
2.会利用合适的统计图表研究生活中的例子.
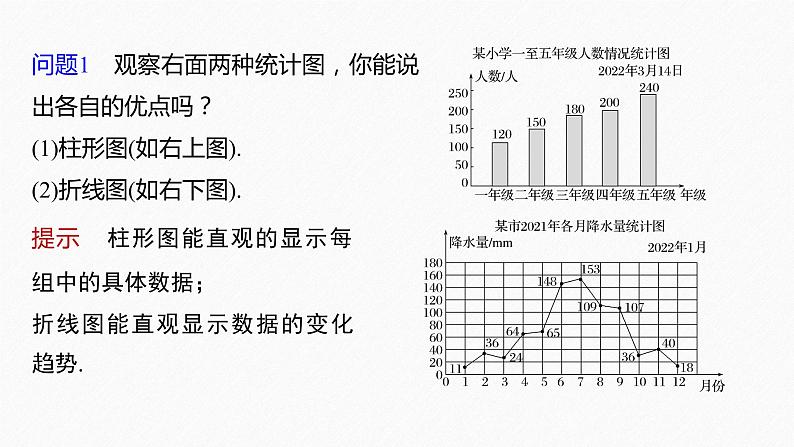
美国历届总统中，就任时年纪最小的是罗斯福，于1901年就任，当时年仅42岁；就任时年纪最大的是拜登，于2021年1月20日就任，年龄是79岁.下面按时间顺序(从1789年的华盛顿到2021年的拜登，共46任)给出了历届美国总统就任时的年龄：57,61,57,57,58,57,61,54,68,51,49,64,50,48,65,52,56,46,54,49,51,47,55,55, 54,42,51,56,55,51,54,51,60,62,43,55,56,61,52,69,64,46,54,48,71,79. 在初中我们用什么图形将各组中的数据形象地在直角坐标系中表示出来？
问题1　观察右面两种统计图，你能说出各自的优点吗？(1)柱形图(如右上图). (2)折线图(如右下图).
提示　柱形图能直观的显示每组中的具体数据；折线图能直观显示数据的变化趋势.
1.柱形图(1)柱形图(也称为条形图)可以形象地比较各种数据之间的 关系.(2)特点：柱形图中，一条轴上显示的是所关注的数据类型，另一条轴上对应的是数量、个数或者比例，柱形图中每一矩形都是 的.2.折线图一般地，如果数据是随时间变化的，想了解数据的 情况，可将数据用折线图来表示.
(1)当数据量很大时一般选用柱形图，它能更直观地反映数据分布的大致情况，并能清晰地表示出各个区间的具体数目，但是柱形图会损失数据的部分信息.(2)折线图能够表现出数据的变化趋势，但不能直观反映数据的分布情况.
　　(1)(多选)2021年4月份居民消费的各类商品及服务价格环比(与3月份相比)变动情况，如下：则下列叙述正确的是A.八大类消费价格环比呈现四涨四平B.其他用品和服务环比涨幅最大C.生活用品及服务和医疗保健价格环　比涨幅相同D.4月份居民消费平均价格环比持平
在八大类消费价格中，食品烟酒、衣着、居住、交通和通信持平，另外四类分别上涨，A正确；其中其他用品和服务环比涨幅最大，为0.4%，B正确；
生活用品及服务和医疗保健价格环比涨幅均为0.1%，C正确；居民消费平均价格环比涨幅为(0.1%＋0.3%＋0.1%＋0.4%)÷8＝0.112 5%，D错误.
(2)(多选)汽车的“燃油效率”是指汽车每消耗1 L汽油行驶的里程，如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.下列叙述中错误的是A.消耗1 L汽油，乙车最多可行驶5 kmB.以相同速度行驶相同路程，三辆车中， 甲车消耗汽油最多C.甲车以80 km/h的速度行驶1 h，消耗8 L汽油D.某城市机动车最高限速80 km/h，相同条件下，在该市用乙车比用丙车 更省油
从图可知消耗1 L汽油，乙车最多可行驶的里程超过了5 km，故A错误；以相同速度行驶相同路程，三辆车中，甲车燃油效率最高，消耗汽油最少，故B错误；若甲车以80 km/h的速度行驶，由图可知，
“燃油效率”为10 km/L，所以行驶1 h，消耗8 L汽油，所以C正确；若某城市机动车最高限速80 km/h，从图可知，丙车比乙车“燃油效率”高，所以在相同条件下，丙车比乙车省油，D错误.
(1)柱形图中，各小矩形宽相等.(2)注意横、纵轴的意义.(3)由柱形图可以作出折线图：取各小矩形上边的中点，再用线段连接，取各小矩形下边的中点并标注上数字，要说明标注数字所对应的数据类型.
　　　(1)某班计划开展一些课外活动，全班有40名学生报名参加，他们就乒乓球、足球、跳绳、羽毛球4项活动的参加人数做了统计，绘制了柱形图如图所示，那么参加羽毛球活动的人
数的频率是________.
由图可知，参加羽毛球活动的人数为4，所以频率为 ＝0.1.
(2)据报道，某咨询公司对1 500个家庭进行了关于奶粉市场的调查，如图是关于每月购买奶粉袋数的有关数据，则每月购买1袋奶粉的比率同每月购买2袋奶粉的比率合计为A.79.9% B.70.9%C.38.8% D.32.1%
根据折线图，每月购买1袋奶粉和每月购买2袋奶粉的比率分别为38.8%和32.1%，故所求值为38.8%＋32.1%＝70.9%.
问题2　观察扇形图(如图)，你能说出它的优点吗？
提示　扇形图能直观地显示各部分所占总体的百分比.
扇形图扇形图也称为饼图、饼形图，它可以形象地表示出各部分数据在全部数据中所占的 情况.扇形图中，每一个扇形的圆心角以及弧长，都与这一部分表示的数据大小成 .
扇形图可以直观地反映出各种情况所占的比例，但是看不出具体数据的多少.
　　某企业三个分厂生产同一种电子产品，三个分厂的产量分布如图所示，现在用分层抽样的方法从三个分厂生产的产品中共抽取100件进行使
用寿命的测试，则第一分厂应抽取的件数为____；测试结果为第一、二、三分厂取出的产品的平均使用寿命分别为1 020小时，980小时，1 030小时，估计这个企业生产的产品的平均使用寿命为________小时.
在扇形图中，部分数据在全部数据中的比例等于对应扇形的圆心角度数与360°之比，等于对应扇形的弧长与周长之比，也等于对应扇形面积与圆面积之比.
　　　已知某地区人口总数为125万，具体分布如图，近期，卫计委拟针对18到60岁的人群开展新冠疫苗接种工作，抽样发现，他们中有80%的人符合接种的健康要求.截止3月底，已有30%符合健康要求的人接种了第一剂，据要求，这部分人需要在4月份接种第二剂，剩余70%符合健康
要求的人需在4月份接种第一剂，5月份接种第二剂.则该地区4月份需要________万剂疫苗.
18到60岁的人数为125×(1－0.15－0.15)＝125×0.7＝87.5(万)，其中符合接种的健康要求的人数为87.5×0.8＝70(万)，所以需要70万剂疫苗.
问题3　林业部门在植树前，为了保证树苗的质量，从同一种树的甲、乙两批树苗中各抽取了10株树苗进行检测，量出它们的高度如下(单位：cm)：甲：37,21,31,20,29,19,32,23,25,33；乙：10,30,47,27,46,14,26,10,44,46.你能用适当的统计图表示上面的数据吗？
提示　如图所示，中间的数字表示每株树苗高度的十位数，两边的数字分别表示个位数.
茎叶图一般来说，茎叶图中，所有的茎都竖直排列，而叶沿 排列.茎叶图也可以只表示一组数.“叶”是从“茎”的旁边生长出来的数.茎叶图通常用来记录两位数的数据，把两位数的十位数字作为“茎”，个位数字作为“叶”，茎相同者共用一个茎，茎按从小到大的顺序从上往下排列.将一组数整理成茎叶图后，如果每一行的数都是按从大到小(或从小到大)顺序排列，则从中可以方便地看出这组数的最值、中位数等数字特征.
(1)茎叶图的优点与不足①优点：一是原始数据信息在图中能够保留，所有数据信息都可以从茎叶图中得到；二是茎叶图中的数据可以随时记录，随时添加，方便记录与表示.②不足：当样本数据较多时，茎叶图就显得不太方便、直观、清晰.(2)茎叶图的作用①从茎叶图中还可以看出一组数的分布情况，从而可以得到一些额外的信息.如数据大部分集中在哪个区间，或极小分布在哪个区间.
②可以估计出数据在某区间的集中程度及数据的平均数所在的区间.③还可以估计出数据相对分散或集中的程度及数据平均数、方差的相对大小.④对于样本数据较少，但较为集中的一组数据；若数据是两位整数，则将十位数字作茎，个位数字作叶；若数据是三位整数，则将百位、十位数字作茎，个位数字作叶；若样本数据是小数，则将整数部分作茎，小数部分作叶.
　　某中学高二(2)班甲、乙两名学生自进入高中以来，每次数学考试成绩情况如下：甲：95,81,75,91,86,89,71,65,76,88,94,110,107；乙：83,86,93,99,88,103,98,114,98,79,78,106,101.画出两人数学成绩的茎叶图，并根据茎叶图对两人的成绩进行比较.
甲、乙两人数学成绩的茎叶图如图所示.
从这个茎叶图上可以看出，乙同学的得分情况是大致对称的，叶主要集中在8,9,10的茎上；
甲同学的得分情况也是大致对称，叶主要集中在7,8,9的茎上.所以乙同学的成绩总体情况比甲同学好.
茎叶图的画法步骤(1)将每个数据分为茎(高位)和叶(低位)两部分.(2)将最小的茎和最大的茎之间的数按从小到大的顺序从上到下列出，茎相同者共用一个茎，再画上竖线作为分界线.(3)将各个数据的叶写在其茎右(左)侧.
　　　(1)从甲、乙两个城市分别随机抽取16台自动售货机，对其销售额进行统计，统计数据用茎叶图表示(如图所示)，设甲、乙两组数据的平均数分别为　 　　，中位数分别为m甲，m乙，则
由茎叶图知，甲的平均数为(5＋6＋8＋10＋10＋14＋18＋18＋22＋25＋27＋30＋30＋38＋41＋43)÷16＝21.562 5，乙的平均数为(10＋12＋18＋20＋22＋
23＋23＋27＋31＋32＋34＋34＋38＋42＋43＋48)÷16＝28.562 5，所以 .甲的中位数为(18＋22)÷2＝20，乙的中位数为(27＋31)÷2＝29，所以m甲