高中数学人教B版 (2019)必修 第二册6.2.3 平面向量的坐标及其运算课文ppt课件

这是一份高中数学人教B版 (2019)必修 第二册6.2.3 平面向量的坐标及其运算课文ppt课件，共60页。PPT课件主要包含了共线向量定理的应用，反思感悟，－10，向量在三角形中的应用，由①②可得m＝3，随堂演练，课时对点练，所以c＝3a－2b，8－15，又∵λ∈01等内容，欢迎下载使用。

会利用向量的有关知识去解决平面向量的综合问题.　
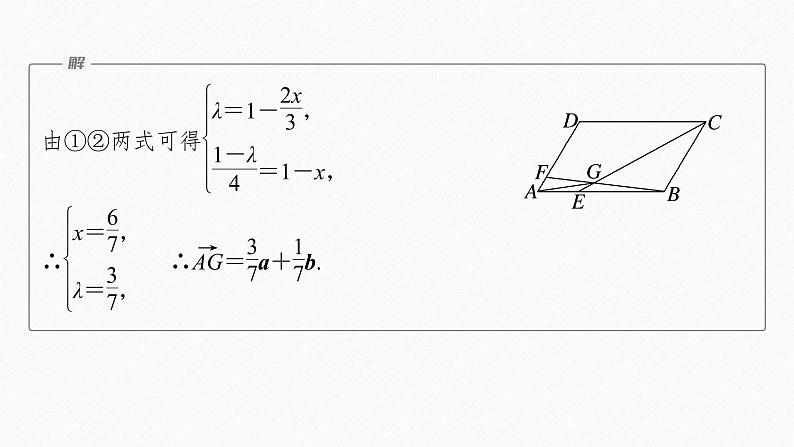
本题的解法中由两组三点共线(F，G，B以及E，G，C三点在一条直线上)，利用平面内三点共线构造方程组求解，避免了用向量的加法和平面向理基本定理解答本题的复杂运算，达到了简化解题过程的目的.
平面向量基本定理的应用
方法一　如图，取AB的中点G，连接DG，CG，
平面向量基本定理离不开向量的线性运算.
由题意，得∠AOC＝90°，故以O为坐标原点，OC，OA所在直线分别为x轴，y轴建立平面直角坐标系如图所示，
向量线性运算中的最值与范围问题
由P，B，C三点共线得，
利用向量的概念及基本运算，将所求问题转化为相应的等式关系，然后用均值不等式求最值.
　　　如图所示，A，B，C是圆O上的三点，CO的延长线与BA的延长线交于圆O外一点D.若　　　　　　　 ，则m＋n的取值范围是________.
由题意知，点M为△ABC的重心，连接AM并延长交BC于点D(图略).
(2)已知△ABC满足 (其中k是非零常数)，则△ABC的形状一定是A.等边三角形 B.钝角三角形C.等腰三角形 D.直角三角形
∴AB＝AC，∴△ABC为等腰三角形.
充分利用向量知识找到三角形中边或角之间的关系是解题的突破口.
设AC的中点为M，BC的中点为N，
1.(多选)下列结论正确的是
∴(k－4)(12－k)－7(k－10)＝0，整理得k2－9k－22＝0，解得k＝－2或k＝11，C正确；
对于D，∵A，B，C三点共线，
∴x＋y＝1，D正确.
以D为原点，DC边所在直线为x轴，DA边所在直线为y轴建立平面直角坐标系(图略).
5.已知在直角梯形ABCD中，AD∥BC，∠ADC＝90°，AD＝2，BC＝1，P是腰DC上的动点，则 的最小值为________.
以D为原点，分别以DA，DC所在直线为x轴，y轴建立如图所示的平面直角坐标系，设DC＝a，DP＝x(0≤x≤a)，∴D(0,0)，A(2,0)，C(0，a)，B(1，a)，P(0，x)，
1.设{e1，e2}是平面内所有向量的一组基底，则下面四组向量中，不能作为基底的是A.{e1＋e2，e1－3e2}B.{e1＋6e2，e1＋e2}C.{e1＋2e2,2e1－e2}D.{3e1－4e2,6e1－8e2}
对于D，有2(3e1－4e2)＝6e1－8e2，即两向量共线，不符合基底的要求；显然，对于A，B，C，不存在实数λ∈R，使e1＋e2＝λ(e1－3e2)，e1＋6e2＝λ(e1＋e2)，e1＋2e2＝λ(2e1－e2)成立，即两向量不共线，故它们均可作为基底.
2.已知向量a，b，c在正方形网格中的位置如图所示，用基底{a，b}表示c，则A.c＝2a－3b B.c＝－2a－3bC.c＝－3a＋2b D.c＝3a－2b
如图建立直角坐标系，设正方形网格的边长为1，则A(1,0)，B(2,1)，C(0,4)，D(7,1)，所以a＝(1,1)，b＝(－2,3)，c＝(7，－3)，设向量c＝ma＋nb，则c＝ma＋nb＝(m－2n，m＋3n)＝(7，－3)，
A.A，B，C三点共线 B.A，B，D三点共线C.A，C，D三点共线 D.B，C，D三点共线
4.已知e1，e2是平面上的两个不共线向量，向量a＝2e1＋e2，b＝me1＋3e2，若a∥b，则实数m等于A.6 　　　　　B.－6 　　　　　C.3 　　　　　D.
设b＝ka，则me1＋3e2＝k(2e1＋e2)＝2ke1＋ke2，
＝(8，－15).所以点P的坐标为(8，－15).
以点A为原点，AB所在的直线为x轴，过点A且垂直于AB的直线为y轴建立平面直角坐标系(图略)，则A(0,0)，B(8,0)，D(2, )，
过点D作AB的垂线交AB于点D′，如图所示，在Rt△ADD′中，由∠BAD＝45°可知，AD′＝3，根据题意得各点坐标为A(0,0)，B(6,0)，D(3,3)，
A.x＝－2，y＝－1 B.x＝－2，y＝1C.x＝2，y＝－1 D.x＝2，y＝1
过点C作CD∥OB交AO的延长线于点D，连接BC，如图所示.因为∠AOB＝60°，OB⊥OC，所以∠COD＝30°，
所以四边形OBCD为平行四边形，
所以x＝－2，y＝1.
根据题意可作出如图所示的几何图形，
∵点C在∠AOB内，且∠AOC＝30°，
所以点O与点D重合，即△ABC的外接圆的圆心是边BC的中点，
故圆O的面积为π·52＝25π.
∵a>0，b>0.若A，B，C三点共线，
即(a－1)e1＋e2＝x(be1－2e2)，∵e1，e2是平面内两个不共线的向量，
由于C，M，B三点共线，