高中数学人教B版 (2019)必修 第二册4.6 函数的应用(二)多媒体教学ppt课件

这是一份高中数学人教B版 (2019)必修 第二册4.6 函数的应用(二)多媒体教学ppt课件，共51页。
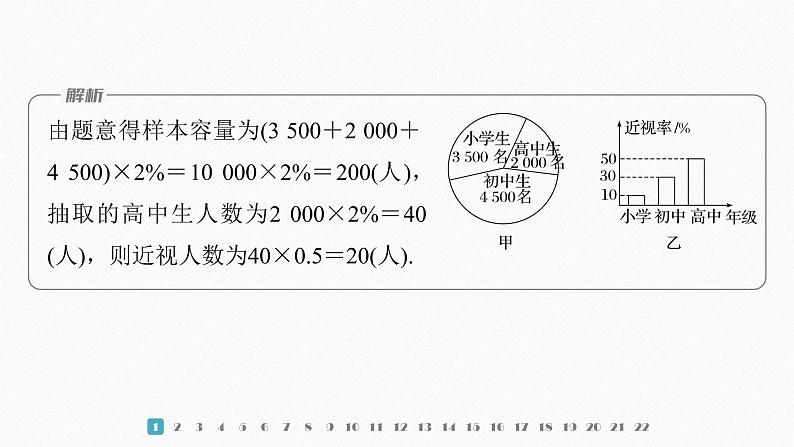
一、单项选择题(本大题共8小题，每小题5分，共40分)1.已知某地区中小学生人数和近视情况分别如图甲和图乙所示.为了了解该地区中小学生的近视形成原因，用分层抽样的方法抽取2%的学生进行调查，则样本容量和抽取的高中生近视人数分别为A.100,10 B.100,20C.200,10 D.200,20
由题意得样本容量为(3 500＋2 000＋ 4 500)×2%＝10 000×2%＝200(人)，抽取的高中生人数为2 000×2%＝40(人)，则近视人数为40×0.5＝20(人).
2.某学校有教师200人，男学生1 200人，女学生1 000人.现用分层抽样的方法从全体师生中抽取一个容量为n的样本，若女学生一共抽取了80人，则n的值为A.193 　　　　　B.192 　　　　　C.191 　　　　　D.190
3.已知随机事件A，B，C中，A与B互斥，B与C对立，且P(A)＝0.3，P(C)＝0.6，则P(A＋B)等于A.0.3 　　　　　B.0.6 　　　　　C.0.7 　　　　　D.0.9
因为这P(C)＝0.6，事件B与C对立，所以P(B)＝0.4，又P(A)＝0.3，A与B互斥，所以P(A＋B)＝P(A)＋P(B)＝0.3＋0.4＝0.7.
4.抛掷一枚质地均匀的骰子，落地后记事件A为“奇数点向上”，事件B为“偶数点向上”，事件C为“2点或4点向上”则在上述事件中，互斥但不对立的共有A.3对 　　　　　B.2对 　　　　　C.1对 　　　　　D.0对
抛掷一枚质地均匀的骰子，落地后记事件A为“奇数点向上”，事件B为“偶数点向上”，事件C为“2点或4点向上”，事件A与事件B是对立事件；事件A与事件C是互斥但不对立事件；事件B与事件C能同时发生，不是互斥事件.故互斥但不对立的共有1对.
5.随机猜测“选择题”的答案，每道题猜对的概率为0.25，则两道选择题至少猜对一道的概率为
6.某人为了检测自己的解题速度，记录了5次解题所花的时间(单位：分)分别为x，y,55,60,50，已知这组数据的平均数为55，方差为　，则|x－y|等于A.1 　　　　　B.2 　　　　　C.3 　　　　　D.4
因为这组数据的平均数为55，方差为 ，所以x＋y＝110，(x－55)2＋(y－55)2＝2.设x＝55＋t，y＝55－t，因为(x－55)2＋(y－55)2＝2，所以2t2＝2，即t2＝1，则|x－y|＝2|t|＝2.
7.在一次年级数学竞赛中，高二(20)班有10%的同学成绩优秀.已知高二(20)班人数占该年级的5%，而年级数学优秀率为2%.现从该年级任意选取一位同学，如果此人成绩优秀，则他来自高二(20)班的概率为A.10% B.15%C.20% D.25%
设该年级的人数为m人，则高二(20)班的人数为m×5%，高二(20)班成绩优秀的人数为m×5%×10%＝0.005m，而该年级的成绩优秀的人数为m×2%＝0.02m，所以所求事件的概率为 ＝0.25＝25%.
8.为了调查某厂2 000名工人生产某种产品的能力，随机抽查了20位工人某天生产该产品的数量，产品数量的分组区间为[10,15)，[15,20)，[20,25)，[25,30)，[30,35]，频率分布直方图如图所示.工厂规定从生产低于20件产品的工人中随机地选取2位工人进行培训，则这2位工人不在同一组的概率是
根据题中频率分布直方图可知产品件数在[10,15)，[15,20)内的人数分别为5×0.02×20＝2,5×0.04×20＝4，设生产产品件数在[10,15)内的2人分别
A，B，生产产品件数在[15,20)内的4人分别是C，D，E，F，则从生产低于20件产品的工人中随机地选取2位工人的样本空间Ω＝{(A，B)，(A，C)，(A，D)，(A，E)，(A，F)，(B，C)，(B，D)，(B，E)，(B，F)，(C，D)，(C，E)，(C，F)，(D，E)，(D，F)，(E，F)}，共包含15个样本点，这15个样本点出现的可能性相等.
2位工人不在同一组的样本点有(A，C)，(A，D)，(A，E)，(A，F)，(B，C)，(B，D)，(B，E)，(B，F)，共8个.则选取的这2人不在同一组的概率为 .
二、多项选择题(本大题共4小题，每小题5分，共20分.全部选对的得5分，部分选对的得2分，有选错的得0分)9.下列事件中，随机事件有A.2023年10月1日，上海市晴天B.在标准大气压下，水在0 ℃时结冰C.从标有1,2,3,4的4张号签中任取一张，恰为1号签D.若x∈R，则|x|19时，y＝3 800＋500(x－19)＝500x－5 700，所以y与x的函数解析式为y＝
(2)若要求“需更换的易损零件数不大于n”的频率不小于0.5，求n的最小值；
由柱状图知，需更换的零件数不大于18的频率为0.46，不大于19的频率为0.7，故n的最小值为19.
(3)假设这100台机器在购机的同时每台都购买19个易损零件，或每台都购买20个易损零件，分别计算这100台机器在购买易损零件上所需费用的平均数，以此作为决策依据，购买1台机器的同时应购买19个还是20个易损零件？
若每台机器在购机的同时都购买19个易损零件，则这100台机器中有70台在购买易损零件上的费用为3 800元，20台的费用为4 300元，10台的费用为4 800元，因此这100台机器在购买易损零件上所需费用的平均数为 ×(3 800×70＋4 300×20＋4 800×10)＝4 000(元).
若每台机器在购机同时都购买20个易损零件，则这100台机器中有90台在购买易损零件上的费用为4 000元，10台的费用为4 500元，因此这100台机器在购买易损零件上所需费用的平均数为 ×(4 000×90＋4 500×10)＝4 050(元).比较两个平均数可知，购买1台机器的同时应购买19个易损零件.