高中数学人教B版 (2019)必修 第一册3.1.3 函数的奇偶性授课ppt课件

这是一份高中数学人教B版 (2019)必修 第一册3.1.3 函数的奇偶性授课ppt课件，共60页。PPT课件主要包含了函数奇偶性的判断，知识梳理，f－x＝fx，有关结论，偶函数，奇函数，注意点，反思感悟，2图像法，利用函数奇偶性求参数等内容，欢迎下载使用。

1.了解函数奇偶性的定义.
2.掌握函数奇偶性的判断和证明方法.
3.会应用奇、偶函数图像的对称性解决简单问题.
在我们的日常生活中，可以观察到许多对称现象，如图，六角形的雪花晶体、建筑物和它在水中的倒影…
而对称美在数学中更是体现的淋漓尽致，今天我们来探究数学中的对称美.
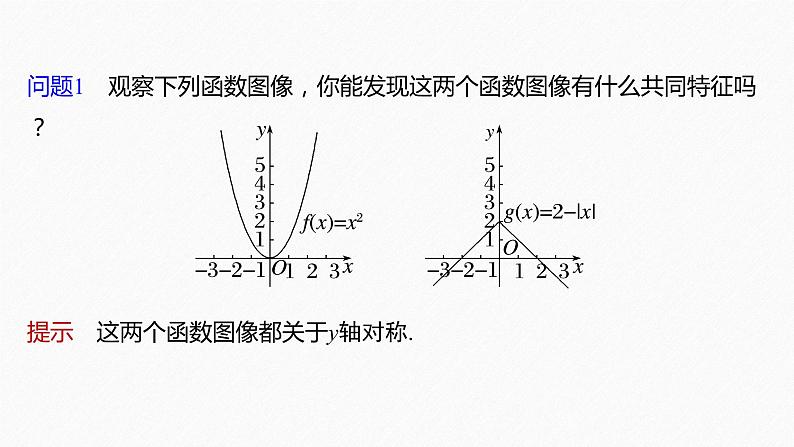
问题1　观察下列函数图像，你能发现这两个函数图像有什么共同特征吗？
提示　这两个函数图像都关于y轴对称.
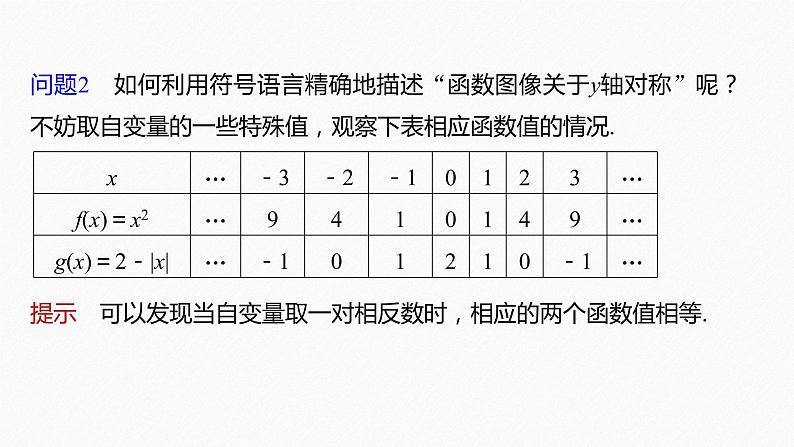
问题2　如何利用符号语言精确地描述“函数图像关于y轴对称”呢？不妨取自变量的一些特殊值，观察下表相应函数值的情况.
提示　可以发现当自变量取一对相反数时，相应的两个函数值相等.
问题3　观察函数f(x)＝x和g(x)＝ 的图像，你能发现这两个函数图像有什么共同特征吗？
提示　可以发现，两个函数的图像都关于原点成中心对称.
函数奇偶性的概念及图像特点
f(－x)＝－f(x)
(1)函数的奇偶性是函数的整体性质；(2)判断函数的奇偶性应先判断定义域是否关于原点对称；(3)偶函数图像关于y轴对称，奇函数图像关于原点对称；(4)若奇函数在原点处有意义，则必有f(0)＝0；(5)既是奇函数又是偶函数的函数有且只有一类，即f(x)＝0，x∈D，D是关于原点对称的实数集.
判断下列函数的奇偶性：(1)f(x)＝2－|x|；
∵函数f(x)的定义域为R，关于原点对称，又f(－x)＝2－|－x|＝2－|x|＝f(x)，∴f(x)为偶函数.
∵函数f(x)的定义域为{－1,1}，关于原点对称，且f(x)＝0，又∵f(－x)＝－f(x)，f(－x)＝f(x)，∴f(x)既是奇函数又是偶函数.
∵函数f(x)的定义域为{x|x≠1}，不关于原点对称，∴f(x)是非奇非偶函数.
f(x)的定义域是(－∞，0)∪(0，＋∞)，关于原点对称.又当x>0时，－x<0，f(－x)＝1－(－x)＝1＋x＝f(x)；当x<0时，－x>0，f(－x)＝1＋(－x)＝1－x＝f(x).综上可知，对于x∈(－∞，0)∪(0，＋∞)，都有f(－x)＝f(x)，f(x)为偶函数.
判断函数奇偶性的两种方法(1)定义法
注意：对于分段函数奇偶性的判断，应分段讨论，要注意根据x的范围取相应的函数解析式.
判断下列函数的奇偶性：
因为函数f(x)的定义域为[0，＋∞)，不关于原点对称，
因为f(x)的定义域为[－1,0)∪(0,1]，关于原点对称.
所以f(x)为奇函数.
因为f(x)的定义域为(－∞，0)∪(0，＋∞)，关于原点对称，又当x>0时，－x<0，则f(－x)＝(－x)2－(－x)＝x2＋x＝f(x)；当x<0时，－x>0，则f(－x)＝(－x)2＋(－x)＝x2－x＝f(x)，综上可知，f(x)是偶函数.
奇、偶函数图像的特征及应用
定义在R上的奇函数y＝f(x)在[0，＋∞)上的图像如图所示.
(1)请在坐标系中补全函数f(x)的图像；
先描出(1,1)，(2,0)关于原点的对称点(－1，－1)，(－2,0)，连线可得f(x)的图像如图.
(2)解不等式xf(x)>0.
xf(x)>0即图像上横坐标、纵坐标同号.结合图像可知，xf(x)>0的解集是(－2,0)∪(0,2).
延伸探究　把本例中的“奇函数”改为“偶函数”，重做该题.
(1)f(x)的图像如图所示.
(2)xf(x)>0的解集是(－∞，－2)∪(0,2).
可以用奇(偶)函数图像关于原点(y轴)对称这一特性去画图、求值、解不等式等.
设奇函数f(x)的定义域为[－5,5]，当x∈[0,5]时，函数y＝f(x)的图像如图所示，则使函数值y<0的x的取值集合为
A.(2,5) B.(－5，－2)∪(2,5)C.(－2,0) D.(－2,0)∪(2,5)
因为原函数是奇函数，所以y＝f(x)在[－5,5]上的图像关于坐标原点对称，由y＝f(x)在[0,5]上的图像，知它在[－5,0]上的图像，如图所示，由图像知，使函数值y<0的x的取值集合为(－2,0)∪(2,5).
(1)若函数f(x)＝ax2＋bx＋3a＋b是偶函数，定义域为[a－1,2a]，则a＝____，b＝____；
因为偶函数的定义域关于原点对称，所以a－1＝－2a，解得a＝ .
结合偶函数图像的特点，得b＝0.
∵f(x)为奇函数，∴f(－x)＝－f(x)，
显然x≠0，整理得x2－(a＋1)x＋a＝x2＋(a＋1)x＋a，故a＋1＝0，得a＝－1.
利用奇偶性求参数的常见类型及策略(1)定义域含参数：奇、偶函数f(x)的定义域为[a，b]，根据定义域关于原点对称，利用a＋b＝0求参数.(2)解析式含参数：根据f(－x)＝－f(x)或f(－x)＝f(x)列式，比较系数即可求解.
(1)若函数f(x)＝x2－|x＋a|为偶函数，则实数a＝_____.
方法一　显然x∈R，由已知得f(－x)＝(－x)2－|－x＋a|＝x2－|x－a|.又f(x)为偶函数，所以f(x)＝f(－x)，即x2－|x＋a|＝x2－|x－a|，即|x＋a|＝|x－a|.又x∈R，所以a＝0.方法二　由题意知f(－1)＝f(1)，则|a－1|＝|a＋1|，解得a＝0.
(2)若定义在(－1,1)上的奇函数f(x)＝ ，则常数m＝___，n＝ ___.
由已知得f(0)＝0，故m＝0.由f(x)是奇函数，知f(－x)＝－f(x)，
∴x2－nx＋1＝x2＋nx＋1，解得n＝0.
1.知识清单： (1)函数奇偶性的概念. (2)奇函数、偶函数的图像特征. (3)利用函数奇偶性求参数.2.方法归纳：特值法、数形结合法.3.常见误区：忽略奇函数、偶函数的定义域关于原点对称.
1.(多选)给定四个函数，其中是奇函数的有
对于A，函数的定义域为R，f(x)＝x3，f(－x)＝(－x)3＝－f(x)，则函数f(x)是奇函数；对于B，函数的定义域不关于原点对称，则函数f(x)为非奇非偶函数；对于C，函数的定义域为R，f(0)＝0＋1＝1≠0，则函数f(x)为非奇非偶函数；
2.函数f(x)＝ －x的图像关于A.y轴对称 B.直线y＝－x对称C.坐标原点对称 D.直线y＝x对称
∵函数的定义域为(－∞，0)∪(0，＋∞)，
因为f(x)是定义在R上的偶函数，
4.下列图像表示的函数是奇函数的是_______，是偶函数的是______(填序号) .
①③关于y轴对称是偶函数，②④关于原点对称是奇函数.
5.已知y＝f(x)是偶函数，且f(x)＝g(x)－2x，g(3)＝3，则g(－3)＝________.
1.(多选)下列函数是偶函数的是A.y＝x(x∈[0,1]) B.y＝3x2C.y＝ ＋x4 D.y＝x|x|
利用偶函数的定义，首先定义域关于原点对称，排除选项A；又偶函数需满足f(－x)＝f(x)，排除选项D；显然BC是偶函数.
2.(多选)若函数f(x)为定义在R上的奇函数，下列结论正确的是A.f(－x)＋f(x)＝0B.f(－x)－f(x)＝－2f(x)C.f(－x)f(x)≤0
∵f(x)为R上的奇函数，∴f(－x)＝－f(x)，∴f(－x)＋f(x)＝0，f(－x)－f(x)＝－2f(x)，f(－x)f(x)＝－f 2(x)≤0，∴A，B，C正确.而D不一定成立，如f(x)＝x，
3.若f(x)＝ax2＋bx＋c(a≠0)是偶函数，则g(x)＝ax3＋bx2＋cx是A.奇函数B.偶函数C.非奇非偶函数D.既是奇函数又是偶函数
因为f(x)＝ax2＋bx＋c是偶函数，所以由f(－x)＝f(x)，得b＝0.所以g(x)＝ax3＋cx.所以g(－x)＝a(－x)3＋c(－x)＝－ax3－cx＝－g(x)，所以g(x)为奇函数.
4.已知函数f(x)是奇函数，函数g(x)是偶函数，且f(－1)＋g(1)＝2，f(1)＋g(－1)＝4，则g(1)等于A.4 B.3C.2 D.1
由题意知f(－1)＋g(1)＝－f(1)＋g(1)＝2，f(1)＋g(－1)＝f(1)＋g(1)＝4.两式相加，解得g(1)＝3.
5.已知定义在R上的偶函数f(x)满足：当x∈[0，＋∞)时，f(x)＝则f(f(－2))的值为A.1 B.3 C.－2 D.－3
∵函数f(x)是定义在R上的偶函数，∴f(－2)＝f(2)＝2－2＝0，f(0)＝0＋1＝1.∴f(f(－2))＝f(0)＝1.
6.已知f(x)，g(x)都是定义域内的非奇非偶函数，而f(x)·g(x)是偶函数，写出满足条件的一组函数，f(x)＝______；g(x)＝_________________.
7.已知函数f(x)＝x3＋ax2＋bx＋c是定义在[2b－5,2b－3]上的奇函数，则的值为_____.
因为f(x)为奇函数，
8.已知f(x)＝x7－ax5＋bx3＋cx＋2，若f(－3)＝－3，则f(3)＝______.
令g(x)＝x7－ax5＋bx3＋cx，则g(x)是奇函数，∴f(－3)＝g(－3)＋2＝－g(3)＋2，又f(－3)＝－3，∴g(3)＝5.又f(3)＝g(3)＋2，所以f(3)＝5＋2＝7.
故函数f(x)的定义域为[－1,0)∪(0,1]，关于原点对称，且有x＋2>0，
故函数f(x)为奇函数.
由条件知f(－x)＋f(x)＝0，
∴c＝0.又f(1)＝2，∴a＋1＝2b.∵f(2)<3，
∵a∈Z，∴a＝0或1.
∵b∈Z，∴a＝1，b＝1，c＝0.
11.已知函数y＝f(x)是偶函数，且图像与x轴有四个交点，则方程f(x)＝0的所有实根之和是A.4 B.2C.1 D.0
因为f(x)是偶函数，且图像与x轴有四个交点，所以这四个交点每组两个关于y轴一定是对称的，故所有实根之和为0.
12.(多选)设函数f(x)和g(x)分别是R上的偶函数和奇函数，则下列结论恒成立的是A.f(x)＋|g(x)|是偶函数B.f(x)－|g(x)|是偶函数C.|f(x)|＋g(x)是偶函数D.|f(x)|－g(x)是奇函数
由f(x)是偶函数，可得f(－x)＝f(x)，由g(x)是奇函数，可得g(－x)＝－g(x)，故|g(x)|为偶函数，∴f(x)＋|g(x)|为偶函数，f(x)－|g(x)|是偶函数.
13.已知偶函数f(x)和奇函数g(x)的定义域都是(－4,4)，且在(－4,0]上的图像如图所示，则关于x的不等式f(x)·g(x)<0的解集是_________________.
(－4，－2)∪(0,2)
14.已知f(x)，g(x)分别是定义在R上的偶函数和奇函数，且f(x)－g(x)＝x3＋x2＋1，则f(1)＋g(1)＝______.
在f(x)－g(x)＝x3＋x2＋1中，令x＝－1，得f(－1)－g(－1)＝1，又f(－1)＝f(1)，g(－1)＝－g(1)，∴f(1)＋g(1)＝1.
A.奇函数B.偶函数C.既是奇函数又是偶函数D.非奇非偶函数
16.(1)已知函数f(x)，x∈R，若对于任意实数x1，x2，都有f(x1＋x2)＋f(x1－x2)＝2f(x1)·f(x2)，求证：f(x)为偶函数；
令x1＝0，x2＝x，得f(x)＋f(－x)＝2f(0)·f(x).①令x2＝0，x1＝x，得f(x)＋f(x)＝2f(0)·f(x).②由①②，得f(x)＋f(－x)＝f(x)＋f(x)，即f(－x)＝f(x)，∴f(x)是偶函数.
(2)设函数f(x)定义在(－l，l)上，证明：f(x)＋f(－x)是偶函数，f(x)－f(－x)是奇函数.