2020-2021学年3.1.1 函数及其表示方法评课课件ppt

这是一份2020-2021学年3.1.1 函数及其表示方法评课课件ppt，共60页。PPT课件主要包含了函数的三种表示方法，函数的表示方法，知识梳理，注意点，1列表法，反思感悟，函数的解析式的求法，方法一配凑法，函数图像的作法及应用，函数的图像等内容，欢迎下载使用。

1.了解函数的三种表示方法及各自的优缺点，会根据不同需要选择恰当的方法表示函数.
2.掌握求函数解析式的常用方法.
3.会作函数的图像并从图像上获取有用信息.
如果一个人极有才华，我们会用“才高八斗”来形容；如果一个人兼有文武才能，我们会用“出将入相”来形容；如果一个人是稀有而可贵的人才，我们会用“凤毛麟角”来形容；如果一个人品行卓越，天下绝无仅有，我们会用“斗南一人”来形容，那么对于呈现出来的不同函数，是否也会有不同的表示方法呢？让我们一起来探究吧.
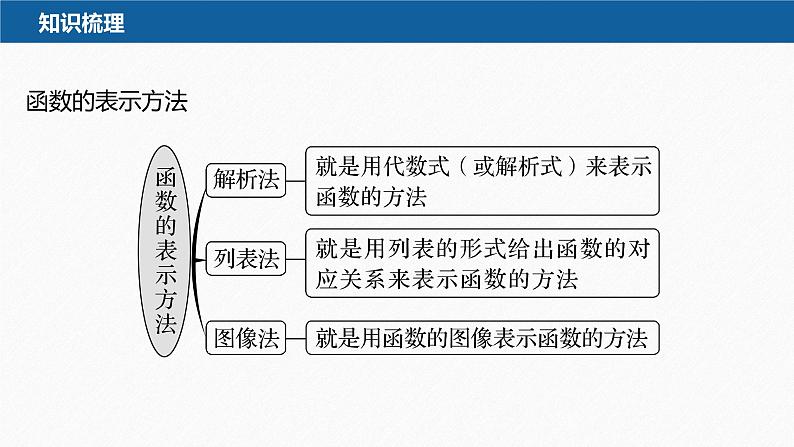
问题　结合初中所学以及上节课的几个问题，你能总结出函数的几种表示方法？
提示　解析法，列表法，图像法.
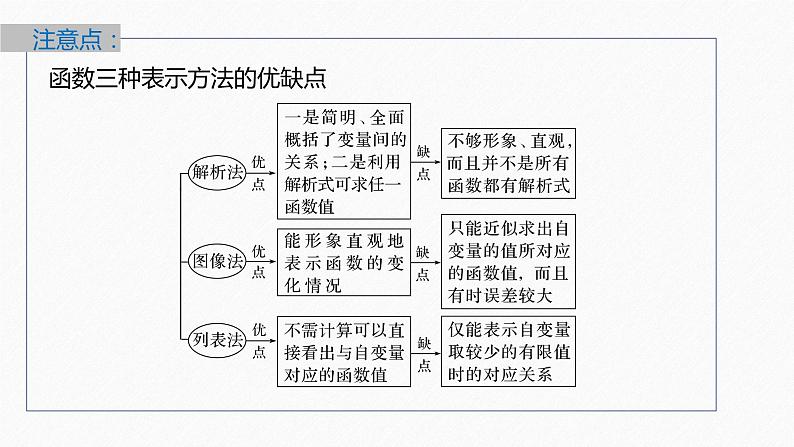
函数三种表示方法的优缺点
某商场新进了10台4K高清电视，每台售价3 000元，试求售出台数x(x为正整数)与收款数y之间的函数关系，分别用列表法、图像法、解析法表示出来.
(2)图像法：如图所示.
(3)解析法：y＝3 000x，x∈{1,2,3，…，10}.
应用函数三种表示方法应注意以下三点(1)解析法必须注明函数的定义域.(2)列表法必须罗列出部分(或全部)自变量与函数值的对应关系.(3)图像法要注意是否连续.
某问答游戏的规则是：共5道选择题，基础分为50分，每答错一道题扣10分，答对不扣分，试分别用列表法、图像法、解析法表示一个参与者的得分y与答错题目道数x(x∈{0,1,2,3,4,5})之间的函数关系.
(1)该函数关系用列表法表示为
(2)该函数关系用图像法表示，如图.
(3)该函数关系用解析法表示为y＝50－10x(x∈{0,1,2,3,4,5}).
(1)已知f(x)是一次函数，且f(f(x))＝9x＋4，求f(x)的解析式；
设f(x)＝kx＋b(k≠0)，则f(f(x))＝k(kx＋b)＋b＝k2x＋kb＋b＝9x＋4.
∴f(x)＝3x＋1或f(x)＝－3x－2.
∴f(x)＝x2－1(x≥1).方法二　(换元法)
∴f(x)＝x2－1(x≥1).
求函数解析式的常用方法(1)换元法(有时可用“配凑法”)：已知函数f(g(x))的解析式，求f(x)的解析式可用换元法(或“配凑法”)，即令g(x)＝t，反解出x，然后代入f(g(x))中求出f(t)，从而求出f(x).(2)待定系数法：若已知函数的类型，可用待定系数法求解，即由函数类型设出函数解析式，再根据条件列方程(组)，通过解方程(组)求出待定系数，进而求出函数解析式.
(3)消元法(或解方程组法)：在已知式子中，含有关于两个不同变量的函数，而这两个变量有着某种关系，这时就要依据两个变量的关系，建立一个新的关于这两个变量的式子，由两个式子建立方程组，通过解方程组消去一个变量，得到目标变量的解析式.
(1)已知函数f(x)是二次函数，且f(0)＝1，f(x＋1)－f(x)＝2x＋2，求f(x)；
(待定系数法)设f(x)＝ax2＋bx＋c(a≠0).∵f(0)＝1，∴c＝1.又∵f(x＋1)－f(x)＝2x＋2，∴a(x＋1)2＋b(x＋1)＋1－(ax2＋bx＋1)＝2x＋2，整理，得2ax＋(a＋b)＝2x＋2.由恒等式的性质，知上式中对应项的系数相等，
∴f(x)＝x2－16(x≥4).∴f(x2)＝x4－16(x≥2或x≤－2).方法二　(换元法)
∴f(t)＝(t－4)2＋8(t－4)＝t2－16(t≥4)，即f(x)＝x2－16(x≥4).∴f(x2)＝x4－16(x≥2或x≤－2).
一般地，将函数y＝f(x)，x∈A中的自变量x和对应的函数值y，分别看成平面直角坐标系中点的横坐标与纵坐标，则满足条件的点(x，y)组成的集合F称为 ，即F＝ .
{(x，y)|y＝f(x)，x∈A}
(1)如果F是函数y＝f(x)的图像，则图像上任意一点的坐标(x，y)都满足函数关系y＝f(x)；反之，满足函数关系y＝f(x)的点(x，y)都在函数的图像F上.(2)实际作图时，经常先描出函数图像上一些有代表性的点，然后再根据有关性质作出函数图像，这称为描点作图法.
作出下列函数的图像并求出其值域：(1)y＝2x＋1，x∈[0,2]；
当x∈[0,2]时，图像是直线y＝2x＋1的一部分，如图，观察图像可知，其值域为[1,5].
(3)y＝x2＋2x，x∈[－2,2].
当－2≤x≤2时，图像是抛物线y＝x2＋2x的一部分，如图，
由图可得函数的值域是[－1,8].
函数y＝f(x)图像的画法(1)若y＝f(x)是已学过的基本初等函数，则描出图像上的几个关键点，直接画出图像即可，有时需要根据定义域进行取舍.(2)若y＝f(x)不是所学过的基本初等函数之一，则要按：①列表；②描点；③连线三个基本步骤作出y＝f(x)的图像.
作出下列函数的图像并求出其值域.(1)y＝x＋2，|x|≤3；
因为|x|≤3，所以函数的图像为线段，而不是直线，如图(1).
观察图像可知，其值域为[－1,5].
(2)y＝x2－2，x∈Z且|x|≤2.
因为x∈Z且|x|≤2，所以函数的图像是五个孤立的点，如图(2).
观察图像可知，其值域为{－2，－1,2}.
1.知识清单： (1)函数的三种表示方法. (2)函数解析式的求法. (3)函数图像的画法和应用.2.方法归纳：配凑法、换元法、待定系数法、数形结合法.3.常见误区：求函数解析式时易忽视定义域.
1.若f(x)＝3x－4，g(x－1)＝f(x)，则g(x)等于A.3x－3 B.3x－5C.3x－1 D.3x＋4
∵g(x－1)＝3x－4＝3(x－1)－1，∴g(x)＝3x－1.
2.已知函数f(x)，g(x)分别由下表给出.
则f(g(1))的值为______；当g(f(x))＝2时，x＝______.
由给出函数关系的表格，知g(1)＝3，∴f(g(1))＝f(3)＝1.由于g(2)＝2，∴f(x)＝2，∴x＝1.
3.已知函数f(x)是一次函数，且其图像过A(－2,0)，B(1,5)两点，则f(x)的解析式为_____________.
4.已知函数f(x)的图像如图所示，其中点A，B的坐标分别为(0,3)，(3,0)，则f(f(0))＝______.
结合题图可得f(0)＝3，则f(f(0))＝f(3)＝0.
5.函数f(x)的图像如图所示，则f(x)的定义域是______________，值域是________.
[－1,0)∪(0,2]
1.下表表示y是x的函数，则函数的值域是
A.[2,5] B.{2,3,4,5}C.(0,20] D.N＋
由表格可知，y的值为2,3,4,5.故函数的值域为{2,3,4,5}.
2.已知函数y＝f(x)的对应关系如下表，函数y＝g(x)的图像是如图的曲线ABC，其中A(1,3)，B(2,1)，C(3,2)，则f(g(2))的值为
由函数g(x)的图像知，g(2)＝1，则f(g(2))＝f(1)＝2.
A.3　　　B.2　　　C.1　　　D.0
A.1　　　B.3　　　C.15　　　D.30
4.(多选)若一次函数的图像经过点A(1,6)和B(2,8)，则该函数的图像还可能经过的点的坐标为
设一次函数的解析式为y＝kx＋b(k≠0)，
所以此函数的解析式为y＝2x＋4，故A，C选项的坐标符合此函数的解析式.
5.甲、乙两人在一次赛跑中，路程s与时间t的函数关系如图所示，则下列说法正确的是A.甲比乙先出发B.乙比甲跑的路程多C.甲、乙两人的速度相同D.甲先到达终点
由图像可以看出，甲、乙的出发时间相同，甲、乙两人所走的路程相同，即s甲＝s乙，故可排除A，B；
由图像的横坐标可看出，甲用的时间小于乙用的时间，故甲先到达终点，而两人的路程相同，所以甲的速度大于乙的速度，故D正确，C错误.
6.已知函数f(x)的图像如图所示，则此函数的定义域是________，值域是________.
结合图像，知函数f(x)的定义域为[－3,3]，值域为[－2,2].
7.已知f(3x－1)＝4x＋2，则f(2)＝_____.
因为f(3x－1)＝4x＋2，所以f(2)＝f(3×1－1)＝4×1＋2＝6.
8.当x为任意实数时，有f(x)＋2f(－x)＝2x＋6，则f(x)＝__________.
∵x∈R，f(x)＋2f(－x)＝2x＋6，①∴f(－x)＋2f(x)＝－2x＋6，②由②×2－①，得3f(x)＝－6x＋6，∴f(x)＝－2x＋2.
9.已知函数f(x)是一次函数，若f(f(x))＝4x＋8，求f(x)的解析式.
设f(x)＝ax＋b(a≠0)，则f(f(x))＝f(ax＋b)＝a(ax＋b)＋b＝a2x＋ab＋b.又f(f(x))＝4x＋8，∴a2x＋ab＋b＝4x＋8，
10.画出函数f(x)＝－x2＋2x＋3的图像，并根据图像回答下列问题：(1)比较f(0)，f(1)，f(3)的大小；
因为函数f(x)＝－x2＋2x＋3的定义域为R，列表：
描点，连线，得函数图像如图：
因为f(0)＝3，f(1)＝4，f(3)＝0，所以f(3)(2)若x1根据图像，容易发现当x1(3)求函数f(x)的值域.
根据图像，可以看出函数的图像是以(1,4)为顶点，开口向下的抛物线，因此，函数的值域为(－∞，4].
11.小明骑车上学，开始时匀速行驶，途中因交通堵塞停留了一段时间后，为了赶时间加快速度行驶.与以上事件吻合得最好的图像是
距学校的距离应逐渐减小，由于小明先是匀速行驶，故前段是直线段，途中停留时距离不变，后段加速，直线段比前段下降的快，故应选C.
12.已知二次函数f(x)＝ax2＋bx＋c满足a>b>c且a＋b＋c＝0，那么它的图像是图中的
∵a>b>c且a＋b＋c＝0，∴a>0，c<0，且f(1)＝0.
13.已知a，b为常数，若f(x)＝x2＋4x＋3，f(ax＋b)＝x2＋10x＋24，则5a－b＝_____.
由f(x)＝x2＋4x＋3，f(ax＋b)＝x2＋10x＋24，得(ax＋b)2＋4(ax＋b)＋3＝x2＋10x＋24，即a2x2＋(2ab＋4a)x＋b2＋4b＋3＝x2＋10x＋24，
14.一个弹簧不挂物体时长12 cm，挂上物体后会伸长，伸长的长度与所挂物体的质量成正比.如果挂上3 kg物体后弹簧总长是13.5 cm，则弹簧总长y(cm)与所挂物体质量x(kg)之间的函数解析式为_________________，若悬挂弹簧的总长变为15 cm，则悬挂的物体的质量是_____kg.
设所求函数解析式为y＝kx＋12(k≠0)，把x＝3，y＝13.5代入，
当y＝15时，可求得x＝6.
15.(多选)一水池有2个进水口，1个出水口，进出水速度如图甲、乙所示.某天0点到6点，该水池的蓄水量如图丙所示(至少打开一个水口).给出以下4个论断，其中正确的是A.0点到3点只进水不出水B.3点到4点不进水只出水 C.3点到4点只有一个进水口进水D.4点到6点不进水也不出水
由题意可知在0点到3点这段时间，每小时进水量为2，即2个进水口同时进水且不出水，所以A 正确；从丙图可知3点到4点水量减少了1，所以应该是有一个进水口进水，同时出水口也出水，故B错，C正确；当两个进水口同时进水，出水口也同时出水时，水量保持不变，故D错.