
还剩9页未读,
继续阅读
初中数学浙教版八年级上册2.3 等腰三角形的性质定理教课ppt课件
展开
这是一份初中数学浙教版八年级上册2.3 等腰三角形的性质定理教课ppt课件,共17页。PPT课件主要包含了想一想,AB≠AC等内容,欢迎下载使用。
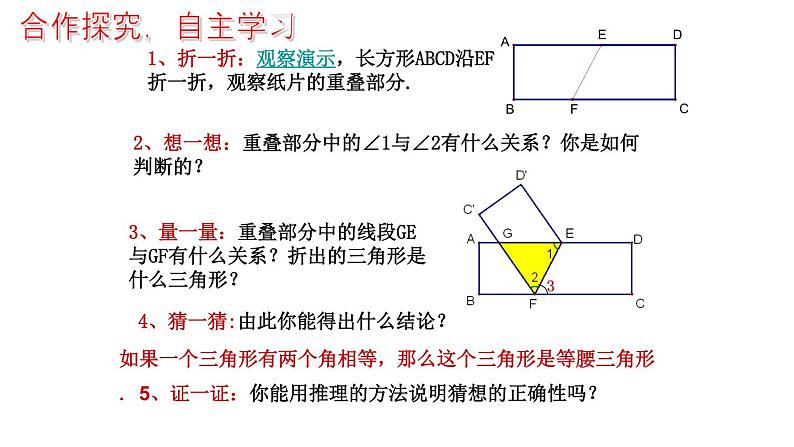
4、猜一猜:由此你能得出什么结论?
3、量一量:重叠部分中的线段GE与GF有什么关系?折出的三角形是什么三角形?
如果一个三角形有两个角相等,那么这个三角形是等腰三角形. 5、证一证:你能用推理的方法说明猜想的正确性吗?
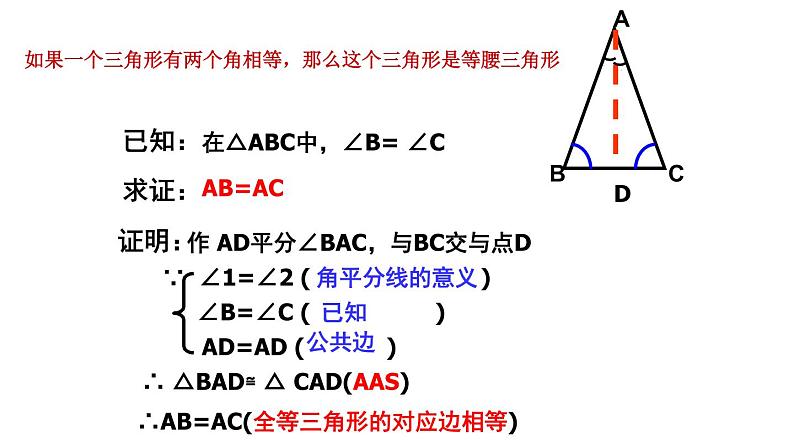
在△ABC中,∠B= ∠C
作 AD平分∠BAC,与BC交与点D
∴ △ BAD≌ △ CAD(AAS)
∴AB=AC(全等三角形的对应边相等)
∵ ∠1=∠2 ( )
AD=AD ( )
如果一个三角形有两个角相等,那么这个三角形是等腰三角形
在同一个三角形中,等角对等边。
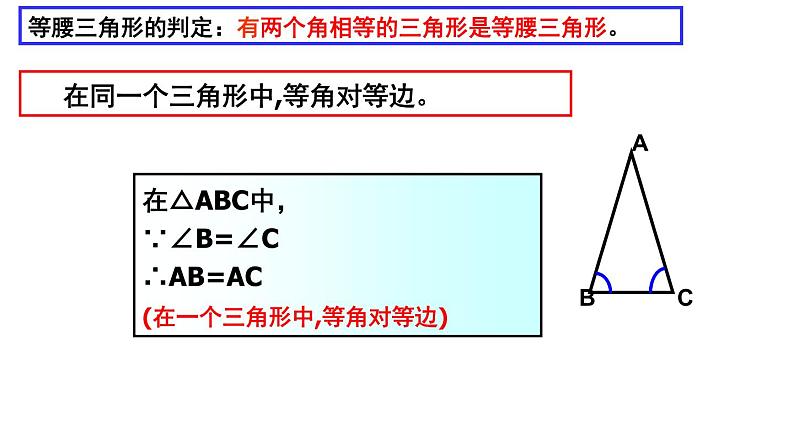
等腰三角形的判定:有两个角相等的三角形是等腰三角形。
在△ABC中,∵∠B=∠C∴AB=AC
(在一个三角形中,等角对等边)
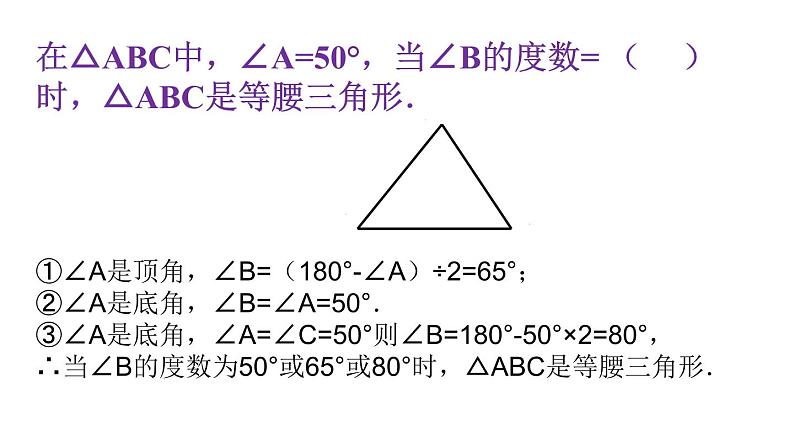
在△ABC中,∠A=50°,当∠B的度数= ( ) 时,△ABC是等腰三角形.
①∠A是顶角,∠B=(180°-∠A)÷2=65°;②∠A是底角,∠B=∠A=50°.③∠A是底角,∠A=∠C=50°则∠B=180°-50°×2=80°,∴当∠B的度数为50°或65°或80°时,△ABC是等腰三角形.
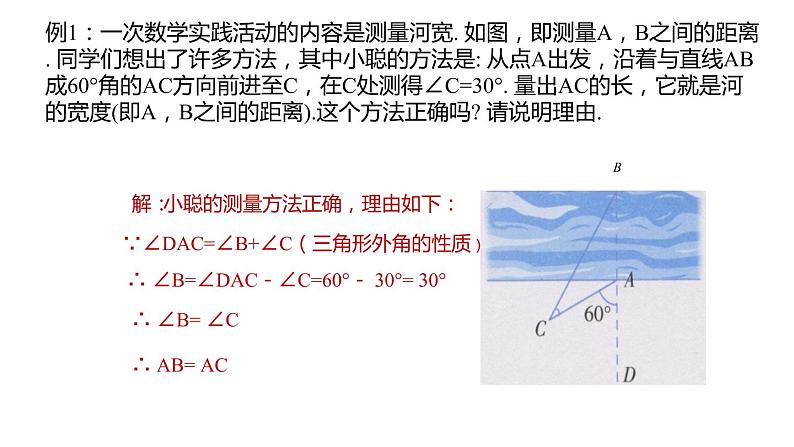
例1:一次数学实践活动的内容是测量河宽. 如图,即测量A,B之间的距离. 同学们想出了许多方法,其中小聪的方法是: 从点A出发,沿着与直线AB成60°角的AC方向前进至C,在C处测得∠C=30°. 量出AC的长,它就是河的宽度(即A,B之间的距离).这个方法正确吗? 请说明理由.
∵∠DAC=∠B+∠C(三角形外角的性质)
∴ ∠B=∠DAC-∠C=60°- 30°= 30°
小聪的测量方法正确,理由如下:
当课本作业课本题堂练习
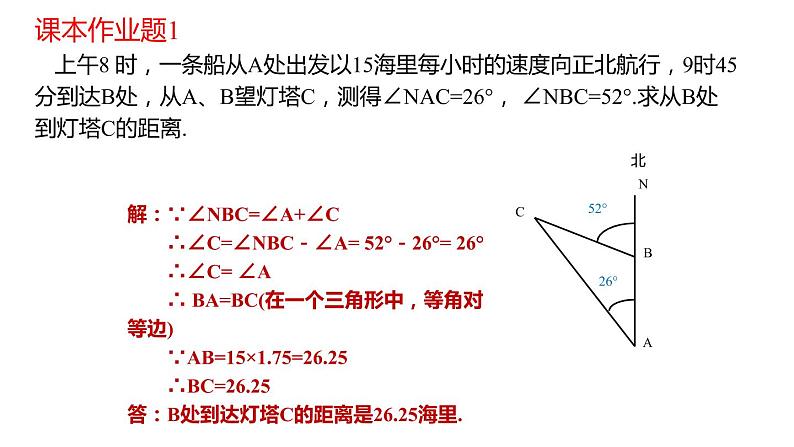
解:∵∠NBC=∠A+∠C ∴∠C=∠NBC-∠A= 52°-26°= 26° ∴∠C= ∠A ∴ BA=BC(在一个三角形中,等角对等边) ∵AB=15×1.75=26.25 ∴BC=26.25答:B处到达灯塔C的距离是26.25海里.
课本作业题1 上午8 时,一条船从A处出发以15海里每小时的速度向正北航行,9时45分到达B处,从A、B望灯塔C,测得∠NAC=26°, ∠NBC=52°.求从B处到灯塔C的距离.
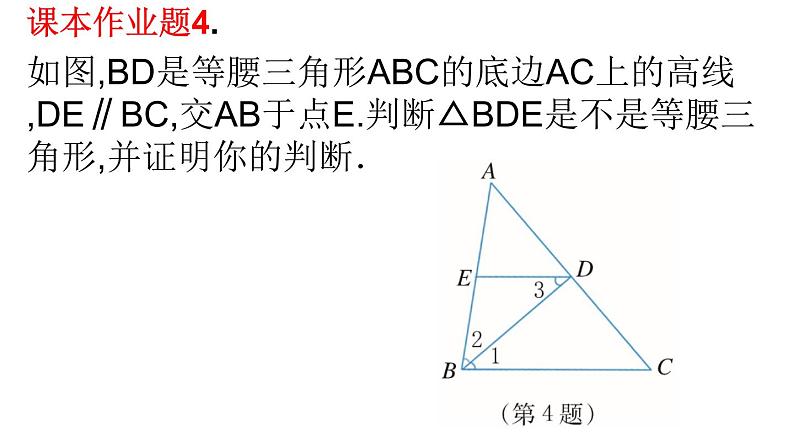
4.如图,BD是等腰三角形ABC的底边AC上的高线,DE∥BC,交AB于点E.判断△BDE是不是等腰三角形,并证明你的判断.
课本作业题4.如图,BD是等腰三角形ABC的底边AC上的高线,DE∥BC,交AB于点E.判断△BDE是不是等腰三角形,并证明你的判断.
等边三角形的三个角有什么性质?
在等腰三角形中,有一种特殊的情况,就是底边与腰相等,这时,三角形三边相等。
我们把三条边都相等的三角形叫做等边三角形(正三角形)。
1、三个角都相等的三角形是等边三角形吗?
∵∠A=∠B=∠C=60 °∴AB=AC=BC (为什么?)∴三角形△ABC是等边三角形.
2、有一个角等于60 °的等腰三角形是等边三角形吗?
假若AB=AC.则∠B=∠C当顶角∠A=60 °时, ∠B=∠C=60 °∴∠A=∠B=∠C=60 °∴ △ABC是等边三角形.当底角∠B=60时,∠C=60 °∠A=180°—(60°+60°)=60°∴ ∠A=∠B=∠C=60 ° ∴ △ABC是等边三角形.
1、三边相等的三角形是等边三角形.
等边三角形的判定方法:
3、有一个角等于60°的等腰三角形是等边三角形.
2、三个角都相等的三角形是等边三角形.
如图, △ABC为等边三角形, ∠ 1= ∠ 2= ∠ 3(1)求∠ BEC的度数.(2) △ DEF为等边三角形吗?为什么?
有两边相等的三角形是等腰三角形
在△ABC中,已知 AB =AC ,BG平分∠ABC,CG平分∠ACB.过点G作直线EF//BC交AB于E,交AC于F.
(2)线段EF和线段EB,FC之间有没有关系?若有,那么是什么关系?
(1)请问图中有多少个等腰三角形?说明理由.
4、猜一猜:由此你能得出什么结论?
3、量一量:重叠部分中的线段GE与GF有什么关系?折出的三角形是什么三角形?
如果一个三角形有两个角相等,那么这个三角形是等腰三角形. 5、证一证:你能用推理的方法说明猜想的正确性吗?
在△ABC中,∠B= ∠C
作 AD平分∠BAC,与BC交与点D
∴ △ BAD≌ △ CAD(AAS)
∴AB=AC(全等三角形的对应边相等)
∵ ∠1=∠2 ( )
AD=AD ( )
如果一个三角形有两个角相等,那么这个三角形是等腰三角形
在同一个三角形中,等角对等边。
等腰三角形的判定:有两个角相等的三角形是等腰三角形。
在△ABC中,∵∠B=∠C∴AB=AC
(在一个三角形中,等角对等边)
在△ABC中,∠A=50°,当∠B的度数= ( ) 时,△ABC是等腰三角形.
①∠A是顶角,∠B=(180°-∠A)÷2=65°;②∠A是底角,∠B=∠A=50°.③∠A是底角,∠A=∠C=50°则∠B=180°-50°×2=80°,∴当∠B的度数为50°或65°或80°时,△ABC是等腰三角形.
例1:一次数学实践活动的内容是测量河宽. 如图,即测量A,B之间的距离. 同学们想出了许多方法,其中小聪的方法是: 从点A出发,沿着与直线AB成60°角的AC方向前进至C,在C处测得∠C=30°. 量出AC的长,它就是河的宽度(即A,B之间的距离).这个方法正确吗? 请说明理由.
∵∠DAC=∠B+∠C(三角形外角的性质)
∴ ∠B=∠DAC-∠C=60°- 30°= 30°
小聪的测量方法正确,理由如下:
当课本作业课本题堂练习
解:∵∠NBC=∠A+∠C ∴∠C=∠NBC-∠A= 52°-26°= 26° ∴∠C= ∠A ∴ BA=BC(在一个三角形中,等角对等边) ∵AB=15×1.75=26.25 ∴BC=26.25答:B处到达灯塔C的距离是26.25海里.
课本作业题1 上午8 时,一条船从A处出发以15海里每小时的速度向正北航行,9时45分到达B处,从A、B望灯塔C,测得∠NAC=26°, ∠NBC=52°.求从B处到灯塔C的距离.
4.如图,BD是等腰三角形ABC的底边AC上的高线,DE∥BC,交AB于点E.判断△BDE是不是等腰三角形,并证明你的判断.
课本作业题4.如图,BD是等腰三角形ABC的底边AC上的高线,DE∥BC,交AB于点E.判断△BDE是不是等腰三角形,并证明你的判断.
等边三角形的三个角有什么性质?
在等腰三角形中,有一种特殊的情况,就是底边与腰相等,这时,三角形三边相等。
我们把三条边都相等的三角形叫做等边三角形(正三角形)。
1、三个角都相等的三角形是等边三角形吗?
∵∠A=∠B=∠C=60 °∴AB=AC=BC (为什么?)∴三角形△ABC是等边三角形.
2、有一个角等于60 °的等腰三角形是等边三角形吗?
假若AB=AC.则∠B=∠C当顶角∠A=60 °时, ∠B=∠C=60 °∴∠A=∠B=∠C=60 °∴ △ABC是等边三角形.当底角∠B=60时,∠C=60 °∠A=180°—(60°+60°)=60°∴ ∠A=∠B=∠C=60 ° ∴ △ABC是等边三角形.
1、三边相等的三角形是等边三角形.
等边三角形的判定方法:
3、有一个角等于60°的等腰三角形是等边三角形.
2、三个角都相等的三角形是等边三角形.
如图, △ABC为等边三角形, ∠ 1= ∠ 2= ∠ 3(1)求∠ BEC的度数.(2) △ DEF为等边三角形吗?为什么?
有两边相等的三角形是等腰三角形
在△ABC中,已知 AB =AC ,BG平分∠ABC,CG平分∠ACB.过点G作直线EF//BC交AB于E,交AC于F.
(2)线段EF和线段EB,FC之间有没有关系?若有,那么是什么关系?
(1)请问图中有多少个等腰三角形?说明理由.













