新教材人教B版步步高学习笔记【同步课件】第二章 章末复习课

这是一份新教材人教B版步步高学习笔记【同步课件】第二章 章末复习课，共37页。

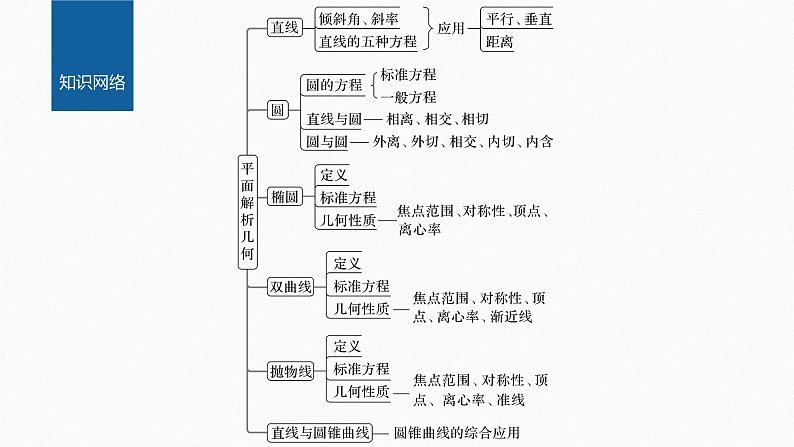
章末复习课第二章　平面解析几何知识网络内容索引直线的方程 一1.直线有五种方程：重点是点斜式、斜截式和一般式方程，直线是平面解析几何的核心内容，求直线的方程一般用公式法和待定系数法，注意五种方程的各自特点和优缺点，在利用待定系数法求直线方程时，选择哪种方程，注意讨论斜率是否存在，截距是否存在，是否为0等特殊情况，以免漏解.2.掌握直线方程的五种形式，会求直线的方程，重点提升数学运算和逻辑推理素养. 已知直线l1：x＋3y－5＝0，直线l2：ax－y＋4＝0(a∈R).(1)若直线l1与直线l2平行，求实数a的值；已知直线l1：x＋3y－5＝0，直线l2：ax－y＋4＝0(a∈R).(2)若直线l1与直线l2垂直，求直线l1与l2的交点坐标.解得a＝3，两直线即直线l1：x＋3y－5＝0，直线l2：3x－y＋4＝0，求直线方程时，要根据给定条件，选择恰当的方法，常用以下两种方法求解(1)直接法：直接选取适当的直线方程的形式，写出结果.(2)待定系数法：先以直线满足的某个条件为基础设出直线方程，再由直线满足的另一个条件求出待定系数，从而求得方程.反思感悟 已知直线l：(2－m)x＋(2m＋1)y＋3m＋4＝0，其中m∈R.(1)求证：直线l恒过定点；直线方程为(2－m)x＋(2m＋1)y＋3m＋4＝0，可化为(2x＋y＋4)＋m(－x＋2y＋3)＝0对任意m都成立，所以直线l恒过定点(－1，－2).(2)当m变化时，求点Q(3,4)到直线的距离的最大值及此时的直线方程.设定点为P(－1，－2)，当m变化，PQ⊥直线l时，点Q(3,4)到直线的距离最大，可知点Q与定点P(－1，－2)的连线的距离就是所求最大值，此时直线l过点P(－1，－2)且与PQ垂直，故直线l的方程为2x＋3y＋8＝0.直线与圆 二1.直线与圆在考试中是常考、必考题型，主要考查直线与圆的三种位置关系以及直线与圆相切求方程、直线与圆相交求弦长等问题.2.掌握判断直线与圆的位置关系的两种方法：代数法和几何法，会求直线与圆相交的弦长，提升逻辑推理和数学运算素养. 已知直线l：kx－y－4k＋3＝0(k∈R)，圆C：x2＋y2－6x－8y＋21＝0.若直线l与圆C交于A，B两点，当弦长AB最短时，求此时直线l的方程.直线l：kx－y－4k＋3＝0可化为(x－4)k－y＋3＝0，所以直线l过定点M(4,3).由圆的几何性质可知，当直线l⊥MC时，弦长最短，因为直线MC的斜率为－1，所以直线l的斜率为1，此时直线l的方程为x－y－1＝0.直线与圆位置关系的判断方法主要有代数法和几何法.一般常用几何法，而不用代数法.因为代数法计算复杂，书写量大，易出错，而几何法较简单.反思感悟 已知圆C1：x2＋y2－2x＋10y－24＝0和圆C2：x2＋y2＋2x＋2y－8＝0相交于A，B两点，则线段AB的长度为______.由圆C1：x2＋y2－2x＋10y－24＝0和圆C2：x2＋y2＋2x＋2y－8＝0相减可得，公共弦的方程为x－2y＋4＝0，圆锥曲线的性质 三1.椭圆、双曲线、抛物线的几何性质是圆锥曲线的核心内容.主要考查由性质求方程，由基本量求离心率、渐近线等，其中离心率是重点，也是难点内容.2.掌握椭圆、双曲线、抛物线的几何性质并会简单应用，提升逻辑推理与数学运算素养.√所以∠PF1F2为锐角，因为△PF1F2是顶角为120°的等腰三角形，但∠PF1F2<∠PF2F1，故∠PF2F1＝120°，所以|PF2|＝|F2F1|＝2c，由余弦定理可得反思感悟常见具体类型(1)已知基本量求离心率e或求离心率e的取值范围.(2)已知圆锥曲线的方程求参数的取值范围.(3)已知曲线的某些性质求曲线方程或求曲线的其他性质.√抛物线y2＝4x的焦点F(1,0)，不妨取其中一条渐近线y＝bx，即bx－y＝0，直线与圆锥曲线的关系 四1.直线与圆锥曲线的位置关系是常考查题型，也是易错题型，特别是直线与双曲线，直线与抛物线相交问题，直线与圆锥曲线相交，求相交弦的弦长是重点内容，圆锥曲线的综合应用是考查的难点.2.掌握直线与圆锥曲线的位置关系，会求相交弦的弦长并能简单的应用，提升逻辑推理和数学运算素养.(1)求C的方程；(2)设直线l的倾斜角为 ，且与C交于A，B两点，求△AOB(O为坐标原点)面积的最大值.则Δ＝300m2－64(5m2－20)>0，解得－80，即直线方程为2x－y－15＝0.(2)已知以抛物线E：y2＝4x的焦点为圆心，与E的准线相切的圆交E于A，B两点，则|AB|等于A.2 B.4 C. D.6√∵y2＝4x，∴焦点F(1,0)，以F为圆心的圆与抛物线准线相切，由抛物线定义及对称性知AB为抛物线通径.∴|AB|＝2p＝4.