2020-2021学年5 确定二次函数的表达式同步达标检测题

这是一份2020-2021学年5 确定二次函数的表达式同步达标检测题，共18页。试卷主要包含了设函数y＝a，某种正方形合金板材的成本y，如图，抛物线的函数表达式是等内容，欢迎下载使用。

2022-2023学年鲁教版九年级数学上册《3.5确定二次函数的表达式》同步练习题（附答案）
一．选择题
1．设函数y＝a（x﹣h）2+k（a，h，k是实数，a≠0），当x＝1时，y＝1；当x＝8时，y＝8，（　　）
A．若h＝4，则a＜0 B．若h＝5，则a＞0
C．若h＝6，则a＜0 D．若h＝7，则a＞0
2．某种正方形合金板材的成本y（元）与它的面积成正比，设边长为x厘米．当x＝3时，y＝18，那么当成本为72元时，边长为（　　）
A．6厘米 B．12厘米 C．24厘米 D．36厘米
3．如图，二次函数y＝x2+bx+c的图象过点B（0，﹣2）．它与反比例函数y＝﹣的图象交于点A（m，4），则这个二次函数的解析式为（　　）

A．y＝x2﹣x﹣2 B．y＝x2﹣x+2 C．y＝x2+x﹣2 D．y＝x2+x+2
4．若二次函数y＝ax2+bx+c的x与y的部分对应值如下表，则当x＝1时，y的值为（　　）
x
﹣7
﹣6
﹣5
﹣4
﹣3
﹣2
y
﹣27
﹣13
﹣3
3
5
3
A．5 B．﹣3 C．﹣13 D．﹣27
5．抛物线的图象如图所示，根据图象可知，抛物线的解析式可能是（　　）

A．y＝x2﹣x﹣2 B．y＝﹣x2﹣x+2
C．y＝﹣x2﹣x+1 D．y＝﹣x2+x+2

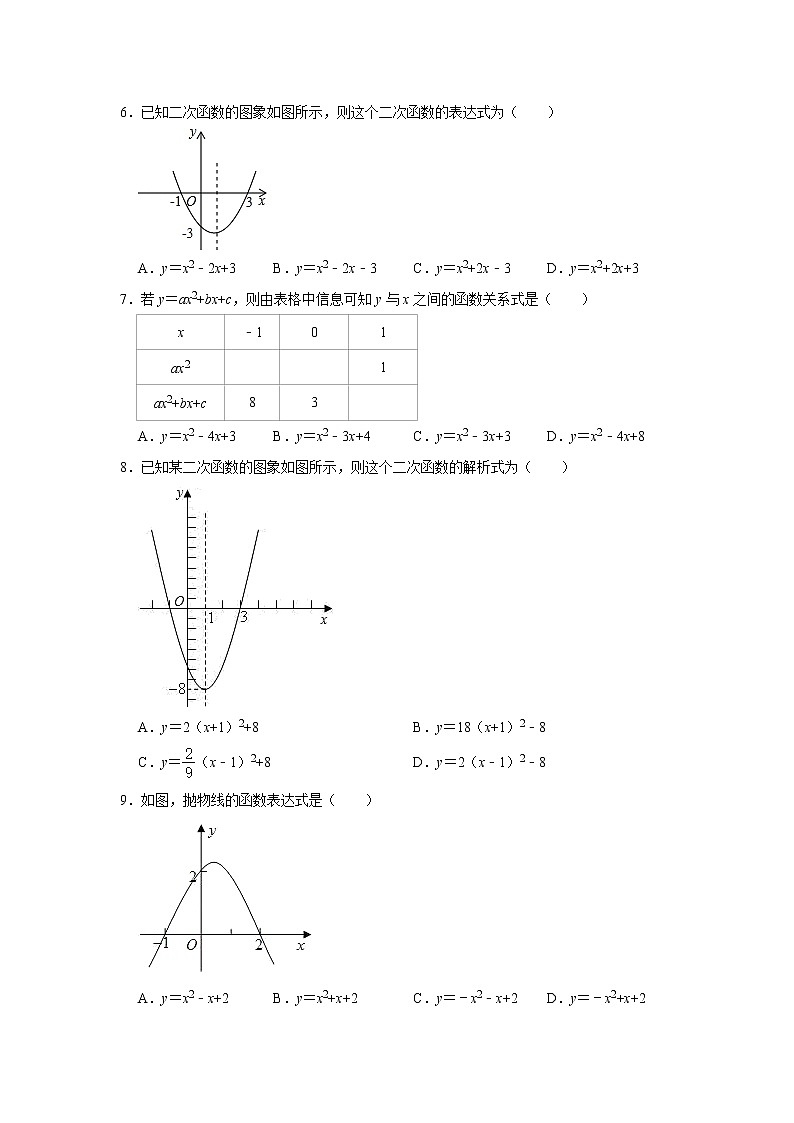
6．已知二次函数的图象如图所示，则这个二次函数的表达式为（　　）

A．y＝x2﹣2x+3 B．y＝x2﹣2x﹣3 C．y＝x2+2x﹣3 D．y＝x2+2x+3
7．若y＝ax2+bx+c，则由表格中信息可知y与x之间的函数关系式是（　　）
x
﹣1
0
1
ax2


1
ax2+bx+c
8
3

A．y＝x2﹣4x+3 B．y＝x2﹣3x+4 C．y＝x2﹣3x+3 D．y＝x2﹣4x+8
8．已知某二次函数的图象如图所示，则这个二次函数的解析式为（　　）

A．y＝2（x+1）2+8 B．y＝18（x+1）2﹣8
C．y＝（x﹣1）2+8 D．y＝2（x﹣1）2﹣8
9．如图，抛物线的函数表达式是（　　）

A．y＝x2﹣x+2 B．y＝x2+x+2 C．y＝﹣x2﹣x+2 D．y＝﹣x2+x+2
10．由表格中信息可知，若设y＝ax2+bx+c，则下列y与x之间的函数关系式正确的是（　　）
x
﹣1
0
1
ax2


1
ax2+bx+c
8
3

A．y＝x2﹣4x+3 B．y＝x2﹣3x+4 C．y＝x2﹣3x+3 D．y＝x2﹣4x+8
11．过（﹣1，0），（3，0），（1，2）三点的抛物线的顶点坐标是（　　）
A．（1，2） B．（1，） C．（﹣1，5） D．（2，）
12．若所求的二次函数图象与抛物线y＝2x2﹣4x﹣1有相同的顶点，并且在对称轴的左侧，y随x的增大而增大，在对称轴的右侧，y随x的增大而减小，则所求二次函数的解析式为（　　）
A．y＝﹣x2+2x﹣5 B．y＝ax2﹣2ax+a﹣3（a＞0）
C．y＝﹣2x2﹣4x﹣5 D．y＝ax2﹣2ax+a﹣3（a＜0）
13．已知二次函数的图象经过（1，0）、（2，0）和（0，2）三点，则该函数的解析式是（　　）
A．y＝2x2+x+2 B．y＝x2+3x+2 C．y＝x2﹣2x+3 D．y＝x2﹣3x+2
14．已知函数y＝ax2+bx+c的图象如图所示，那么函数解析式为（　　）

A．y＝﹣x2+2x+3 B．y＝x2﹣2x﹣3 C．y＝﹣x2﹣2x+3 D．y＝﹣x2﹣2x﹣3
二．填空题
15．如图，在平面直角坐标系中，O为坐标原点，点C为y轴正半轴上的一个动点，过点C的直线与二次函数y＝x2的图象交于A、B两点，且CB＝3AC，P为CB的中点，设点P的坐标为P（x，y）（x＞0），写出y关于x的函数表达式为：　 　．

16．经过A（4，0），B（﹣2，0），C（0，3）三点的抛物线解析式是　 　．
17．已知一个二次函数的图象开口向上，顶点坐标为（0，﹣1 ），那么这个二次函数的解析式可以是 　 　．（只需写一个）
18．已知二次函数y＝x2+bx+c经过点（3，0）和（4，0），则这个二次函数的解析式是　 　．
19．抛物线y＝ax2+bx+c（a≠0）经过点（1，2）和（﹣1，﹣6）两点，则a+c＝　 　．
20．若抛物线y＝ax2+bx+c的顶点是A（2，1），且经过点B（1，0），则抛物线的函数关系式为　 　．
21．如图，四边形ABCD是矩形，A、B两点在x轴的正半轴上，C、D两点在抛物线y＝﹣x2+6x上．设OA＝m（0＜m＜3），矩形ABCD的周长为l，则l与m的函数解析式为　 　．

三．解答题
22．已知抛物线y＝﹣x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C，顶点为D．
（1）求该抛物线的解析式；
（2）连接BC，CD，BD，P为BD的中点，连接CP，则线段CP的长是 　 　．
注：抛物线y＝ax2+bx+c（a≠0）的对称轴是直线x＝﹣，顶点坐标是（﹣，）．



23．如图，抛物线y＝x2+bx+c经过点A（﹣1，0），点B（2，﹣3），与y轴交于点C，抛物线的顶点为D．
（1）求抛物线的解析式；
（2）抛物线上是否存在点P，使△PBC的面积是△BCD面积的4倍，若存在，请直接写出点P的坐标；若不存在，请说明理由．

24．在一条笔直的滑道上有黑、白两个小球同向运动，黑球在A处开始减速，此时白球在黑球前面70cm处．
小聪测量黑球减速后的运动速度v（单位：cm/s）、运动距离y（单位：cm）随运动时间t（单位：s）变化的数据，整理得下表．
运动时间t/s
0
1
2
3
4
运动速度v/cm/s
10
9.5
9
8.5
8
运动距离y/cm
0
9.75
19
27.75
36
小聪探究发现，黑球的运动速度v与运动时间t之间成一次函数关系，运动距离y与运动时间t之间成二次函数关系．
（1）直接写出v关于t的函数解析式和y关于t的函数解析式（不要求写出自变量的取值范围）；
（2）当黑球减速后运动距离为64cm时，求它此时的运动速度；
（3）若白球一直以2cm/s的速度匀速运动，问黑球在运动过程中会不会碰到白球？请说明理由．

25．如图，抛物线y＝a（x﹣2）2+3（a为常数且a≠0）与y轴交于点A（0，）．
（1）求该抛物线的解析式；
（2）若直线y＝kx+（k≠0）与抛物线有两个交点，交点的横坐标分别为x1，x2，当x12+x22＝10时，求k的值；
（3）当﹣4＜x≤m时，y有最大值，求m的值．

26．已知抛物线y＝ax2+bx+3经过点A（1，0）和点B（﹣3，0），与y轴交于点C，P为第二象限内抛物线上一点．
（1）求抛物线的解析式，并写出顶点坐标；
（2）如图，连接PB，PO，PC，BC．OP交BC于点D，当S△CPD：S△BPD＝1：2时，求出点D的坐标．


参考答案
一．选择题
1．解：当x＝1时，y＝1；当x＝8时，y＝8；代入函数式得：，
∴a（8﹣h）2﹣a（1﹣h）2＝7，
整理得：a（9﹣2h）＝1，
若h＝4，则a＝1，故A错误；
若h＝5，则a＝﹣1，故B错误；
若h＝6，则a＝﹣，故C正确；
若h＝7，则a＝﹣，故D错误；
故选：C．
2．解：设y与x之间的函数关系式为y＝kx2，由题意，得
18＝9k，
解得：k＝2，
∴y＝2x2，
当y＝72时，72＝2x2，
∴x＝6．
故选：A．
3．解：将A（m，4）代入反比例解析式得：4＝﹣，即m＝﹣2，
∴A（﹣2，4），
将A（﹣2，4），B（0，﹣2）代入二次函数解析式
得：，
解得：b＝﹣1，c＝﹣2，
则二次函数解析式为y＝x2﹣x﹣2．
故选：A．
4．解：由表可知，抛物线的对称轴为x＝﹣3，
∴当x＝1和x＝﹣7的函数值相等，
∵当x＝﹣7时，y＝﹣27，
∴x＝1时，y＝﹣27．
故选：D．
5．解：A、由图象可知开口向下，故a＜0，此选项错误；
B、抛物线过点（﹣1，0），（2，0），根据抛物线的对称性，顶点的横坐标是，
而y＝﹣x2﹣x+2的顶点横坐标是﹣＝﹣，故此选项错误；
C、y＝﹣x2﹣x+1的顶点横坐标是﹣，故此选项错误；
D、y＝﹣x2+x+2的顶点横坐标是，并且抛物线过点（﹣1，0），（2，0），故此选项正确．
故选：D．
6．解：根据题意，图象与y轴交于负半轴，故c为负数，又四个选项中，B、C的c为﹣3，符合题意，故
设二次函数的表达式为y＝ax2+bx+c，
抛物线过（﹣1，0），（0，﹣3），（3，0），
所以，
解得a＝1，b＝﹣2，c＝﹣3，
这个二次函数的表达式为y＝x2﹣2x﹣3．
故选：B．
7．解：将x＝1，ax2＝1代入y＝ax2得a＝1．
将（﹣1，8），（0，3）分别代入y＝x2+bx+c中得：
，
解得；
∴函数解析式是：y＝x2﹣4x+3．
故选：A．
8．解：由图知道，抛物线的顶点坐标是（1，﹣8）
故二次函数的解析式为y＝2（x﹣1）2﹣8
故选：D．
9．解：根据题意，设二次函数的表达式为y＝ax2+bx+c，
抛物线过（﹣1，0），（0，2），（2，0），
所以，
解得a＝﹣1，b＝1，c＝2，
这个二次函数的表达式为y＝﹣x2+x+2．
故选：D．
10．解：将x＝1，ax2＝1，代入y＝ax2，得a＝1．
将x＝﹣1，a＝1分别代入ax2+bx+c＝8，得1﹣b+c＝8，
将x＝0，a＝1分别代入ax2+bx+c＝3，得c＝3，
则b＝﹣4，
∴函数解析式是：y＝x2﹣4x+3．
故选：A．
11．解：设这个二次函数的解析式是y＝ax2+bx+c，
把（﹣1，0），（3，0），（1，2）代入，
得，
解之得，
所以该函数的解析式为：y＝﹣x2+x+，
顶点坐标是（1，2）．
故选：A．
12．解：抛物线y＝2x2﹣4x﹣1的顶点坐标为（1，﹣3），根据题意得所求的二次函数的解析式的顶点坐标是（1，﹣3），且抛物线开口向下．
A、抛物线开口向下，顶点坐标是（1，﹣4），故选项错误；
B、抛物线开口向上，顶点坐标是（1，﹣3），故选项错误；
C、抛物线开口向下，顶点坐标是（﹣1，﹣3），故选项错误；
D、抛物线开口向下，顶点坐标是（1，﹣3），故选项正确．
故选：D．
13．解：设这个二次函数的解析式是y＝ax2+bx+c，把（1，0）、（2，0）和（0，2）代入得：，解之得；
所以该函数的解析式是y＝x2﹣3x+2．
故选：D．
14．解：由图知：抛物线经过点（﹣1，0），（3，0），（0，3）；
设抛物线的解析式为：y＝a（x+1）（x﹣3），则有：
a（0+1）（0﹣3）＝3，a＝﹣1；
即：y＝﹣（x+1）（x﹣3）＝﹣x2+2x+3，
故选：A．
二．填空题
15．解：过A作AD⊥y轴于D，过B作BE⊥y轴于E，如图：

∵AD⊥y轴，BE⊥y轴，
∴AD∥BE，
∴△ACD∽△BCE，
∴＝＝，
∵CB＝3AC，
∴CE＝3CD，BE＝3AD，
设AD＝m，则BE＝3m，
∵A、B两点在二次函数y＝x2的图象上，
∴A（﹣m，m2），B（3m，9m2），
∴OD＝m2，OE＝9m2，
∴ED＝8m2，
而CE＝3CD，
∴CD＝2m2，OC＝3m2，
∴C（0，3m2），
∵P为CB的中点，
∴P（m，6m2），
又已知P（x，y），
∴，
∴y＝x2；
故答案为：y＝x2．
16．解：根据题意设抛物线解析式为y＝a（x+2）（x﹣4），
把C（0，3）代入得：﹣8a＝3，即a＝﹣，
则抛物线解析式为y＝﹣（x+2）（x﹣4）＝﹣x2+x+3，
故答案为y＝﹣x2+x+3．
17．解：∵抛物线的顶点坐标为（0，﹣1），
∴该抛武线的解析式为y＝ax2﹣1，
又∵二次函数的图象开口向上，
∴a＞0，
∴这个二次函数的解析式可以是y＝2x2﹣1，
故答案为：y＝2x2﹣1．
18．解：设二次函数的解析式为y＝a（x﹣3）（x﹣4），
而a＝1，
所以二次函数的解析式为y＝（x﹣3）（x﹣4）＝x2﹣7x+12．
故答案为y＝x2﹣7x+12．
19．解：把点（1，2）和（﹣1，﹣6）分别代入y＝ax2+bx+c（a≠0）得：
，
①+②得：2a+2c＝﹣4，
则a+c＝﹣2；
故答案为：﹣2．
20．解：设抛物线的解析式为y＝a（x﹣2）2+1，
将B（1，0）代入y＝a（x﹣2）2+1得，
a＝﹣1，
函数解析式为y＝﹣（x﹣2）2+1，
展开得y＝﹣x2+4x﹣3．
故答案为y＝﹣x2+4x﹣3．
21．解：把x＝m代入抛物线y＝﹣x2+6x中，得AD＝﹣m2+6m
把y＝﹣m2+6m代入抛物线y＝﹣x2+6x中，得
﹣m2+6m＝﹣x2+6x
解得x1＝m，x2＝6﹣m
∴C的横坐标是6﹣m，故AB＝6﹣m﹣m＝6﹣2m
∴矩形的周长是l＝2（﹣m2+6m）+2（6﹣2m）
即l＝﹣2m2+8m+12．
三．解答题
22．解：（1）∵抛物线y＝﹣x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，
∴，
解得：，
∴抛物线的解析式为y＝﹣x2+2x+3；
（2）∵y＝﹣x2+2x+3＝﹣（x﹣1）2+4，
∴D（1，4），
把x＝0代入y＝﹣x2+2x+3，得y＝3，
∴C（0，3），
∵P为BD的中点，
∴P（2，2），
∴CP＝＝．
故答案为：．
23．解：（1）∵抛物线y＝x2+bx+c经过点A（﹣1，0），点B（2，﹣3），
∴，
解得b＝﹣2，c＝﹣3，
∴抛物线的解析式：y＝x2﹣2x﹣3；
（2）存在，理由如下：
∵y＝x2﹣2x﹣3＝（x﹣1）2﹣4，
∴D点坐标为（1，4），
令x＝0，则y＝x2﹣2x﹣3＝﹣3，
∴C点坐标为（0，﹣3），
又∵B点坐标为（2，﹣3），
∴BC∥x轴，
∴S△BCD＝×2×1＝1，
设抛物线上的点P坐标为（m，m2﹣2m﹣3），
∴S△PBC＝×2×|m2﹣2m﹣3﹣（﹣3）|＝|m2﹣2m|，
当|m2﹣2m|＝4×1时，
解得m＝1±，
当m＝1+时，m2﹣2m﹣3＝1，
当m＝1﹣时，m2﹣2m﹣3＝1，
综上，P点坐标为（1+，1）或（1﹣，1）．
24．解：（1）设v＝mt+n，将（0，10），（2，9）代入，得，
解得，，
∴v＝﹣t+10；
设y＝at2+bt+c，将（0，0），（2，19），（4，36）代入，得，
解得，
∴y＝﹣t2+10t．
（2）令y＝64，即﹣t2+10t＝64，
解得t＝8或t＝32，
当t＝8时，v＝6；
当t＝32时，v＝﹣6（舍）；
（3）设黑白两球的距离为wcm，
根据题意可知，w＝70+2t﹣y
＝t2﹣8t+70
＝（t﹣16）2+6，
∵＞0，
∴当t＝16时，w的最小值为6，
∴黑白两球的最小距离为6cm，大于0，黑球不会碰到白球．
另解1：当w＝0时，t2﹣8t+70＝0，判定方程无解．
另解2：当黑球的速度减小到2cm/s时，如果黑球没有碰到白球，此后，速度低于白球速度，不会碰到白球．先确定黑球速度为2cm/s时，其运动时间为16s，再判断黑白两球的运动距离之差小于70 cm．
25．解：（1）∵抛物线y＝a（x﹣2）2+3与y轴交于点A（0，），
∴4a+3＝，
∴a＝﹣，
∴y＝﹣（x﹣2）2+3；
（2）∵直线y＝kx+与抛物线有两个交点，
∴kx+＝﹣（x﹣2）2+3，
整理得x2+（3k﹣4）x﹣3＝0，
∴Δ＝（3k﹣4）2+12＞0，
∵x1+x2＝4﹣3k，x1•x2＝﹣3，
∴x12+x22＝（4﹣3k）2+6＝10，
∴k＝或k＝2，
∴k的值为2或；
（3）∵函数的对称轴为直线x＝2，
当m＜2时，当x＝m时，y有最大值，
＝﹣（m﹣2）2+3，
解得m＝，
∴m＝﹣，
当m≥2时，当x＝2时，y有最大值，
∴＝3，
∴m＝，
综上所述，m的值为﹣或．
26．解：（1）将点A（1，0）和点B（﹣3，0）代入函数解析式，
可得，
解得：，
∴y＝﹣x2﹣2x+3，
又∵y＝﹣x2﹣2x+3＝﹣（x+1）2+4，
∴抛物线的顶点坐标为（﹣1，4）；
（2）如图，过点D作DM⊥y轴，

由y＝﹣x2﹣2x+3，当x＝0时，y＝3，
∴C点坐标为（0，3），
设直线BC的解析式为y＝kx+b，将B（﹣3，0），C（0，3）代入，
可得：，
解得：，
∴直线BC的解析式为y＝x+3，
∵S△CPD：S△BPD＝1：2，
∴，，
又∵DM⊥y轴，
∴DM∥OB，
∴，
∴，
解得：OM＝2，
在y＝x+3中，当y＝2时，x＝﹣1，
∴D点坐标为（﹣1，2）．