2022-2023年高中物理竞赛 电场1.4高斯定理 课件

这是一份2022-2023年高中物理竞赛 电场1.4高斯定理 课件，共22页。PPT课件主要包含了对开曲面，对整个球面有，4推广，注意理解，解题步骤，4讨论，场具有轴对称性，面对称或中心对称，③利用上述结果得到，由高斯定理得等内容，欢迎下载使用。
两种取法,通量等值异号.
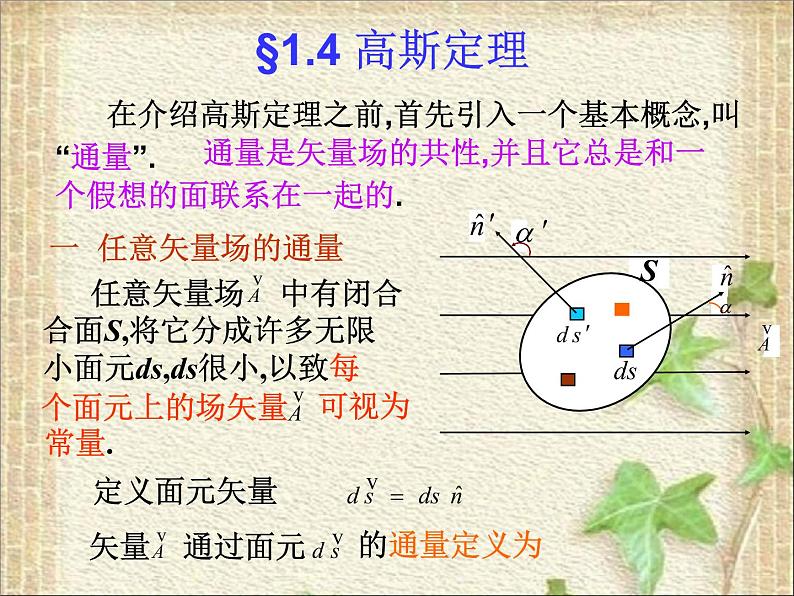
对于闭合曲面,通常规定自内向外的方向为面元法线的正方向,对非闭合曲面,应根据情况事先规定好法线方向.
1、内容及数学表达式（P19）
由库仑定律及场强叠加原理证明其正确性.
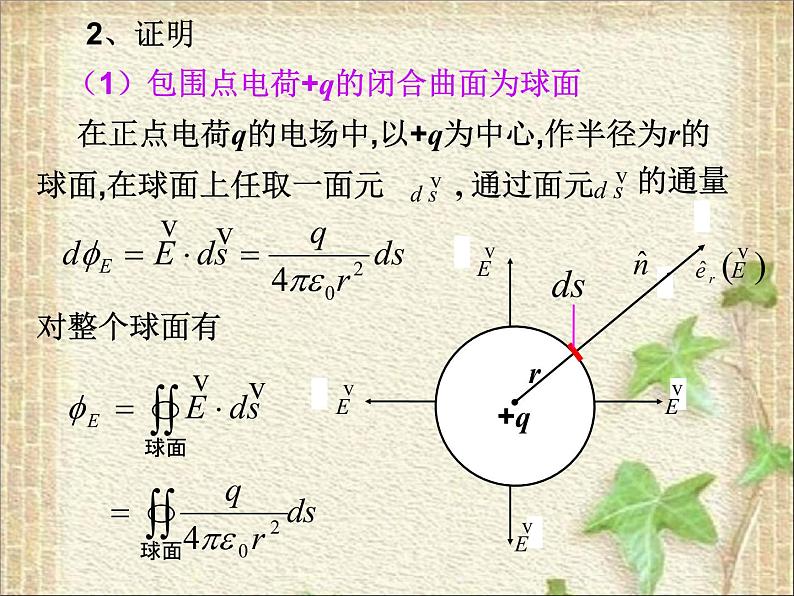
（1）包围点电荷+q的闭合曲面为球面
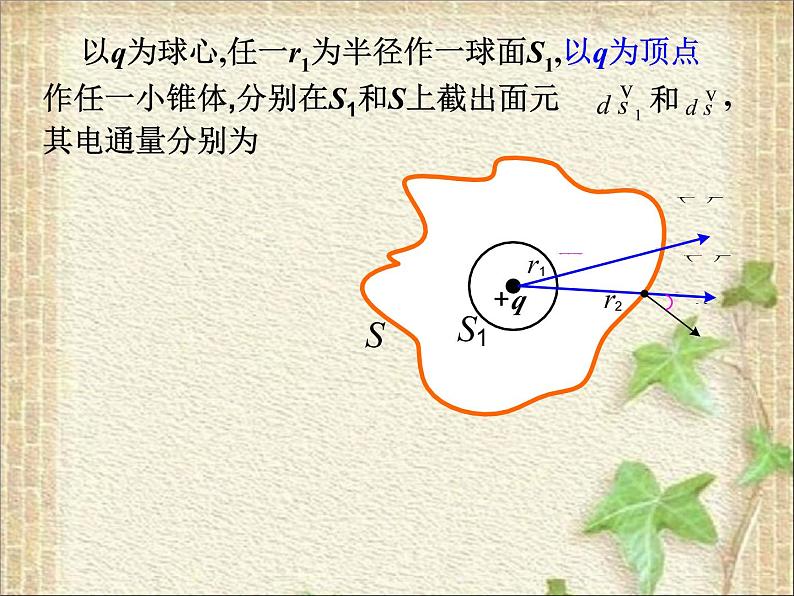
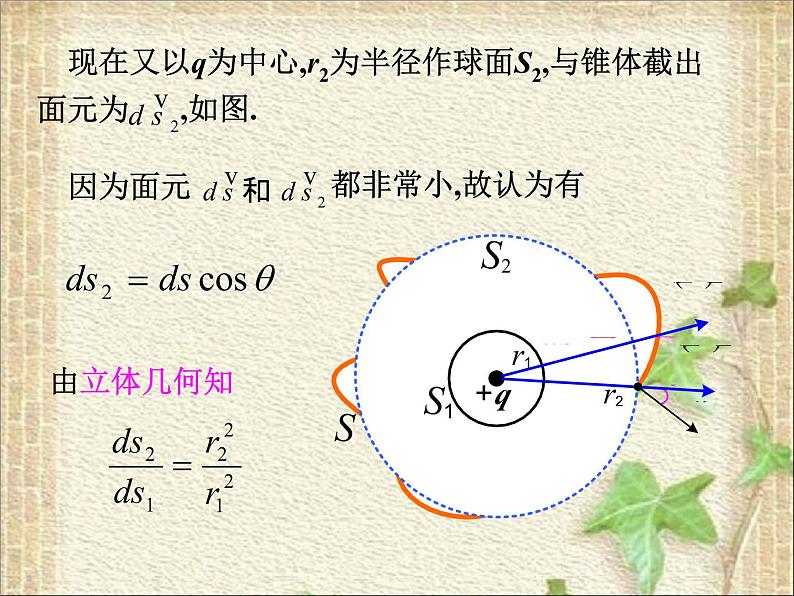
（2）包围点电荷+q的闭合曲面S是任意形状
任意形状的闭合面S,其间有点电荷+q
即包围点电荷q的曲面为任意曲面时,仍能得（4.1）式的结果（既高斯定理仍然成立）.q是负电荷的情况同理可以证明,只需将q换为-q即可.
（3）点电荷q在任意闭合曲面S之外
任意闭合曲面S,在S面上选一闭合曲线L,把S分成S1和S3两部分（非闭合）.
再以L为边线作非闭合曲面S2,使S2分别与S1和S3组成闭合曲向并包围了q,这时
（利用步骤（2）的结果）
（正负电荷都有此结果）
根据场强叠加原理将上述结论进行推广.
①面S内有q1、q2、……qn个点电荷,且它们可正可负
②闭合曲面S外有多个点电荷
③电荷为连续分布的任意带电体
3、对高斯定理的说明
①高斯定理是静电场的基本定理之一,揭示了场和场源的内在联系,它说明静电场是有源场.
②高斯定理和库仑定律可以互相推导,都可以作为静电学的基础,从这点来说,它们是等价的.
对于迅速变化（迅变）电磁场,库仑定律不成立,而高斯定理可以推广到迅速变化的电磁场,所以高斯定理比库仑定律应用更广泛.
使用上有不同的分工：库仑定律（及叠加原理）解决从电荷分布求场强的问题,高斯定理使我们能从场强（场强作为已知的点函数）求出电荷分布.
当带电体与闭合面相交时,带电体不能被看成点电荷.实际上,闭合面把带电体A分成两部分A1和A2,根据高斯定理,只有位于闭合面内的那部分A2才对整个闭合面的电通量有贡献.
四 用高斯定理求场强
（1）分析电场的对称性
（2）根据电场不同的对称性,选取相应的适当的高斯面（高斯面是闭合曲面并过场点）
（3）分别计算通过高斯面的电通量和高斯面内的净电荷量,根据高斯定理列出方程,求出场强的大小.
由叠加原理,P点的总场强必然垂直于棒而离开棒.
根据场强具有轴对称性的特点,选取与细棒同轴的半径为r的封闭圆柱面为高斯面,设柱面高l,通过高斯面的电通量为
其方向垂直于棒而离开棒.
解：用反证法证明无限大带电平面外的场强方向垂直于平面.
高斯面取圆柱面、正方体或长方体的表面
②无限大均匀带电平面的电场中,各点的场强与场点的位置无关,带电平面的两边各形成一个均匀电场.
a、两个带等量同号电荷的无限大平行平面的场强分布
b、两个带等量异号电荷的无限大平行平面的电场分布
解：电场分布具有轴对称性
（和例1无限长带电直线的结果一样）
带电圆柱面内部各点场强等于零.