苏科版七年级上册第5章 走进图形世界5.3 展开与折叠课时作业

这是一份苏科版七年级上册第5章 走进图形世界5.3 展开与折叠课时作业，文件包含课时53展开与折叠解析版docx、课时53展开与折叠原卷版docx等2份试卷配套教学资源，其中试卷共18页， 欢迎下载使用。
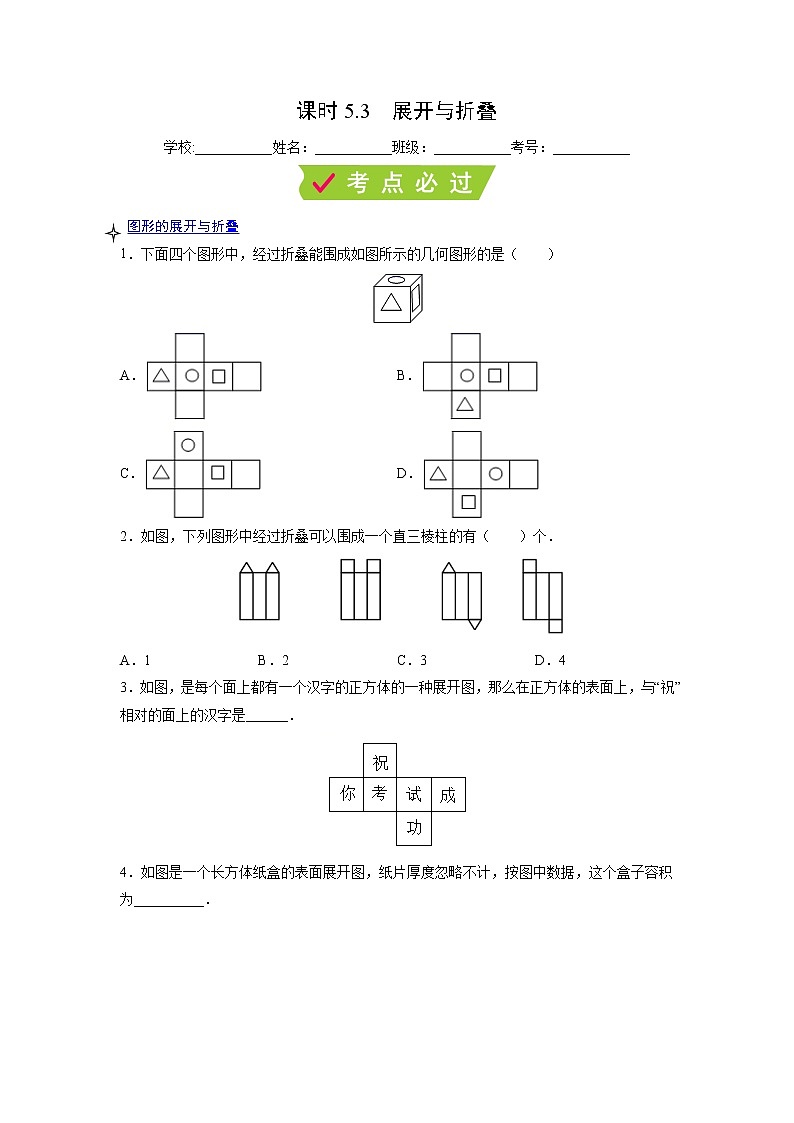
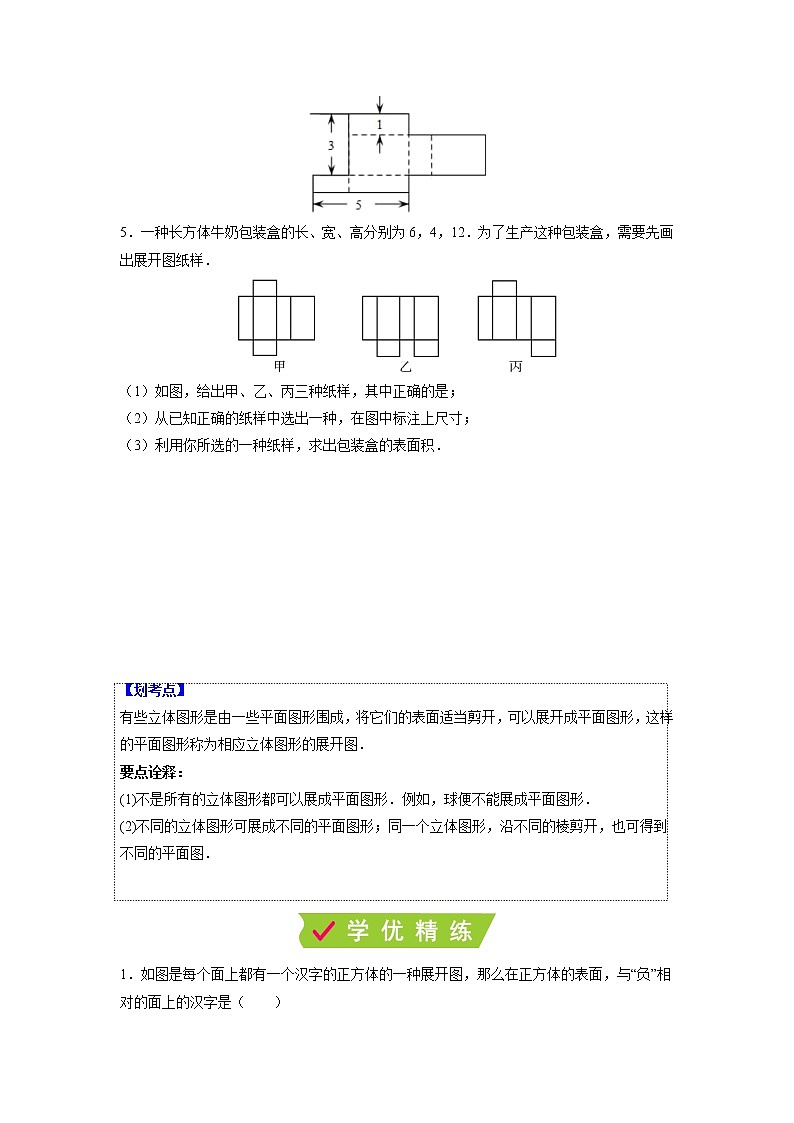
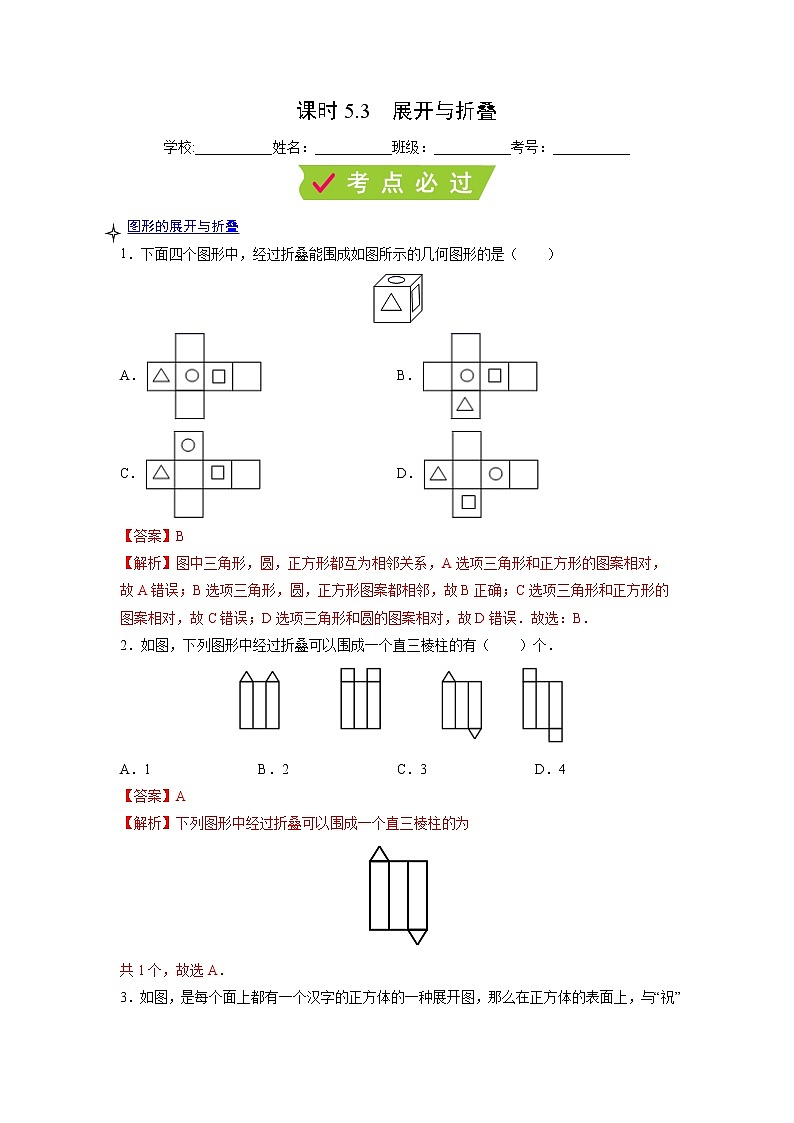
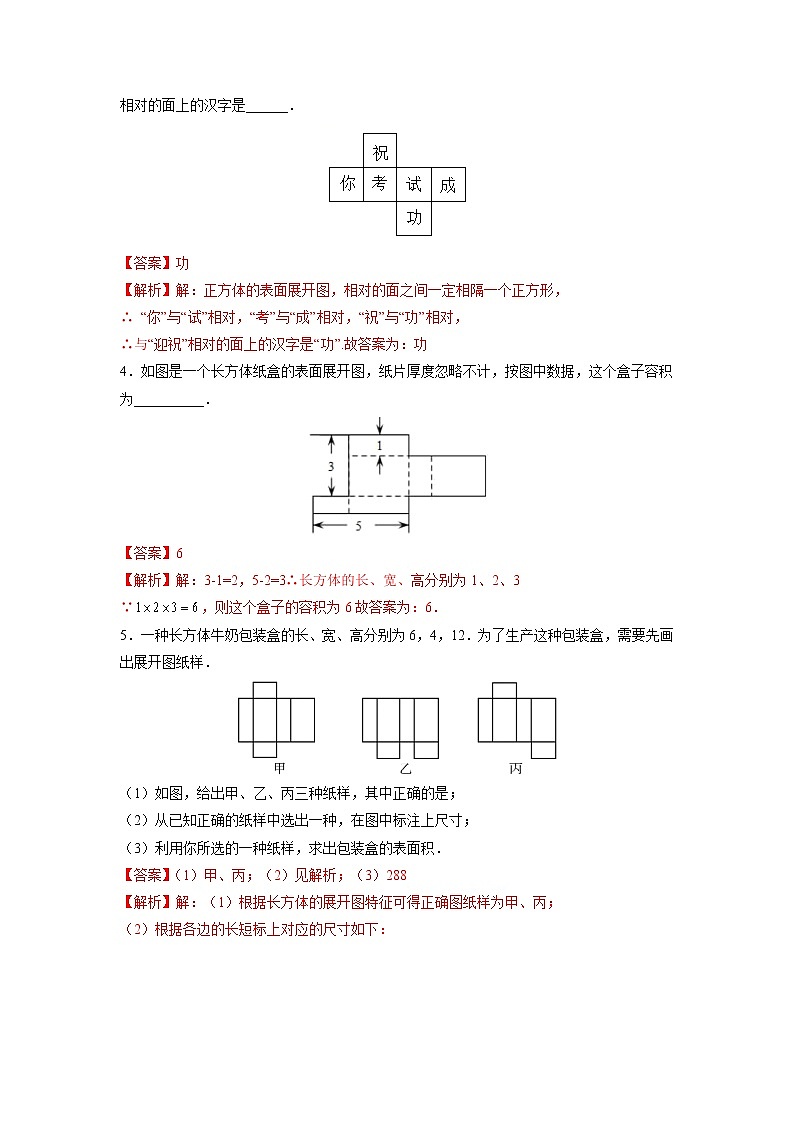
课时5.3  展开与折叠学校:___________姓名：___________班级：___________考号：___________ 图形的展开与折叠1．下面四个图形中，经过折叠能围成如图所示的几何图形的是（    ）A． B．C． D．【答案】B【解析】图中三角形，圆，正方形都互为相邻关系，A选项三角形和正方形的图案相对，故A错误；B选项三角形，圆，正方形图案都相邻，故B正确；C选项三角形和正方形的图案相对，故C错误；D选项三角形和圆的图案相对，故D错误．故选：B．2．如图，下列图形中经过折叠可以围成一个直三棱柱的有（    ）个．A．1 B．2 C．3 D．4【答案】A【解析】下列图形中经过折叠可以围成一个直三棱柱的为共1个，故选A．3．如图，是每个面上都有一个汉字的正方体的一种展开图，那么在正方体的表面上，与“祝”相对的面上的汉字是______．【答案】功【解析】解：正方体的表面展开图，相对的面之间一定相隔一个正方形，∴ “你”与“试”相对，“考”与“成”相对，“祝”与“功”相对，∴与“迎祝”相对的面上的汉字是“功”.故答案为：功4．如图是一个长方体纸盒的表面展开图，纸片厚度忽略不计，按图中数据，这个盒子容积为__________．【答案】6【解析】解：3-1=2，5-2=3∴长方体的长、宽、高分别为1、2、3∵，则这个盒子的容积为6故答案为：6．5．一种长方体牛奶包装盒的长、宽、高分别为6，4，12．为了生产这种包装盒，需要先画出展开图纸样． （1）如图，给出甲、乙、丙三种纸样，其中正确的是； （2）从已知正确的纸样中选出一种，在图中标注上尺寸；（3）利用你所选的一种纸样，求出包装盒的表面积．【答案】（1）甲、丙；（2）见解析；（3）288【解析】解：（1）根据长方体的展开图特征可得正确图纸样为甲、丙；
（2）根据各边的长短标上对应的尺寸如下：

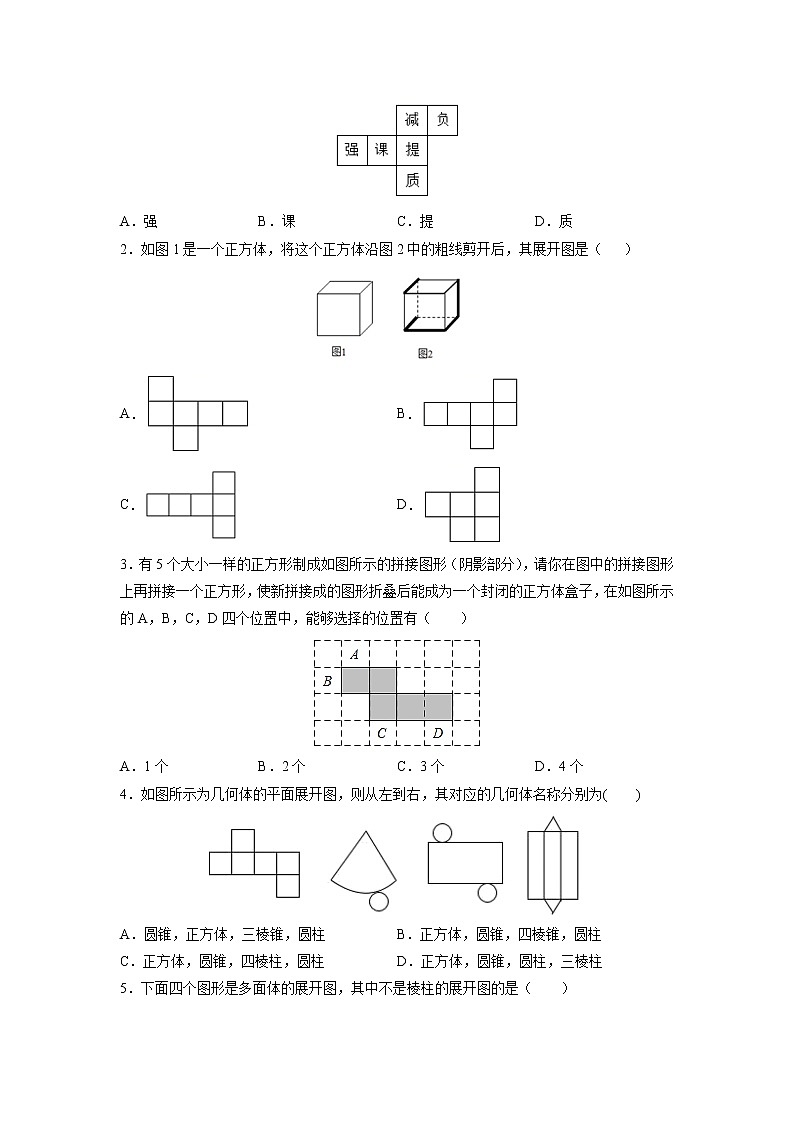
 （3）该包装盒的表面积为2×6×12+2×4×12+2×6×4=144+96+48=288． 【划考点】有些立体图形是由一些平面图形围成，将它们的表面适当剪开，可以展开成平面图形，这样的平面图形称为相应立体图形的展开图．要点诠释：(1)不是所有的立体图形都可以展成平面图形．例如，球便不能展成平面图形．(2)不同的立体图形可展成不同的平面图形；同一个立体图形，沿不同的棱剪开，也可得到不同的平面图． 1．如图是每个面上都有一个汉字的正方体的一种展开图，那么在正方体的表面，与“负”相对的面上的汉字是（    ）A．强 B．课 C．提 D．质【答案】B【解析】解：正方体的表面展开图，相对的面之间一定相隔一个正方形，∴“负”与“课”相对，“减”与“质”相对，“强”与“提”相对，∴与“负”相对的面上的汉字是“课”，故选B．2．如图1是一个正方体，将这个正方体沿图2中的粗线剪开后，其展开图是（   ）A． B．C． D．【答案】C【解析】解：如图1的正方体沿图2中的粗线剪开后，其展开图是：故选：C．3．有5个大小一样的正方形制成如图所示的拼接图形（阴影部分），请你在图中的拼接图形上再拼接一个正方形，使新拼接成的图形折叠后能成为一个封闭的正方体盒子，在如图所示的A，B，C，D四个位置中，能够选择的位置有（　　）A．1个 B．2个 C．3个 D．4个【答案】D【解析】解：如图所示：根据立方体的展开图可知，不能选择图中A的位置接正方形．故选：D．4．如图所示为几何体的平面展开图，则从左到右，其对应的几何体名称分别为(    )A．圆锥，正方体，三棱锥，圆柱 B．正方体，圆锥，四棱锥，圆柱C．正方体，圆锥，四棱柱，圆柱 D．正方体，圆锥，圆柱，三棱柱【答案】D【解析】解：根据几何体的平面展开图，则从左到右，其对应的几何体名称分别为：正方体，圆锥，圆柱，三棱柱．故选D．5．下面四个图形是多面体的展开图，其中不是棱柱的展开图的是（　　）A． B．C． D．【答案】D【解析】A、6个正方形能围成一个正方体，所以，这是正方体的展开图； B、6个长方形可以围成长方体．所以，这是长方体的展开图；C、三个长方形和两个三角形能围成一个三棱柱，所以，这是三棱柱的展开图；D、一个四边形和四个三角形能围成四棱锥，所以，这是四棱锥的展开图；故本选项符合题意．故选：D．6．若要使得图中平面展开图折叠成正方体后，相对面上的两个数之和相等，则的值为______．【答案】12【解析】解：这是一个正方体的平面展开图，共有六个面，可知a与b相对，c与一2相对，3与2相对，∵相对面上两个数之和相等，∴a+b=c-2=3+2，∴a+b=5，c=7，∴a+b+c=12．故答案为：12．7．如图是一个正方体的表面沿着某些棱剪开后展成的一个平面图形，若这个正方体的每两个相对面上的数字的和都是8，则y＝___．【答案】11【解析】解：正方体的表面展开图，相对的面之间一定相隔一个正方形， “-3”与“y”是相对面，∵这个正方体的每两个相对面上的数字的和都是8，∴y＝8-（-3）=11；故答案为：11．8．有一个正六面体骰子，放在桌面上，将骰子沿如图所示的顺时针方向滚动，每滚动90°算一次，则滚动第3次后，骰子朝下一面的点数是 ___．（填数字）【答案】5【解析】解：由前三个正方体的信息可得：1点的对面是6点，2点的对面是5点，3的对面是4，所以滚动第3次后，骰子朝下一面的点数是5.故答案为：5.9．若一个几何体的表面展开图如图所示，则该几何体棱的条数为__________．【答案】15【解析】解：由展开图折叠后可以围成五棱柱．而五棱柱有15条棱，故答案为15．10．如图，该展开图能折叠成的立体图形是________．【答案】圆锥【解析】解：由图形可得，展开图由两部分组成，圆和扇形（半圆），符合这一特征的几何体只有圆锥，圆为圆锥的底面，扇形（半圆）为圆锥的侧面，故答案为圆锥11．用一个长方形的纸片按如图方式制作一个无盖的长方体盒子（在长方形的右边两个角上各剪去一个大小相同的正方形，左上角剪去一个长方形）．设这个长方形的长为a，宽为b，折成的无盖长方体盒子高为c，若a＝7cm，b＝4cm，c＝1cm，则这个无盖长方体盒子的容积是________cm3．【答案】8【解析】解：无盖长方体盒子的高为c=1cm，∴AG=DF=1cm，∴AD=b-2c=4-2=2cm，∵BH=BC=AD=2cm，∴CD=a-c-BH=7-1-2=4cm，∴无盖长方体盒子的长为4cm，宽为2cm，高为1cm，∴这个无盖长方体盒子的容积为：4×2×1=8cm3，故答案为：8．12．如图所示是一个正方体的表面展开图，请回答下列问题：（1）与面A相对的面是________，与面B相对的面是________，与面C相对的面是________；（2）若，，，，且相对两个面所表的代数式的和都相等，分别求D，F代表的代数式．【答案】（1）D，F，E；（2）； ．【解析】解：（1）与面A相对的面是D，与面B相对的面是F，与面C相对的面是E，故答案为：D；F；E；（2）∵A+D=B+F=C+E，∴，∴，=，=，∴，=，=．13．如图所示的长方体的容器，，且这个容器的容积为384立方分米，（1）求这个长方体容器底面边长AB的长为多少分米?（2）若这个长方体的两个底面和侧面都是用铁皮制作的，则制作这个长方体容器需要多少平方分米铁皮?(不计损耗)【答案】（1）分米；（2）平方分米．【解析】解：（1）设分米，则分米，分米，∴立方分米，∴，即，解得：，∴分米；（2）由（1）得分米，∴分米，分米，则长方体的侧面积为，即,∴平方分米，则长方体的底面积为，即，∴平方分米，∴，∴平方分米，答：制作这个长方体容器需要平方分米铁皮．14．如图所示，图1为一个棱长为8的正方体，图2为图1的表面展开图（数字和字母写在外表面上，字母也可以表示数），请根据要求回答问题：（1）如果正方体相对面上的两个数字之和相等，则______，______．（2）如果面“10”是左面，面“6”在前面，则上面是______（填“x”或“y”或“2”）（3）图1中，点M为所在棱的中点，在图2中找点M的位置，直接写出图2中△ABM的面积．【答案】（1）12；8（2）x；（3）16或80【解析】解：（1）∵正方体相对面上的两个数字之和相等∴，∴，，故答案为：12；8（2）若面“10”是左面，面“6”在前面，则上面是“x”（3）因为点M所在的棱为两个面共用，所以它的位置有两种情况，第一种情况如下图：设点M左边的顶点为点D，则 第二种情况如下图：，综上所述，的面积为：16或8015．已知一个直四棱柱的底面边长为5cm的正方形，侧棱长都是8cm，回答下列问题：（1）这个直四棱柱一共有几个面？几个顶点？几条棱？（2）将这个直四棱柱的侧面展开成一个平面图形，这个图形是什么形状？面积是多少？（3）这个直四棱柱的体积是多少？【答案】（1）6，8，12；（2）长方形，160cm2；（3）200cm3【解析】（1）根据直四棱柱的特征可知该直四棱柱有6个面，8个顶点，12条棱；（2）由长方形的性质可知，将这个直四棱柱的侧面展开形成一个平面图形，这个图形为长方形，长方形的宽为该直四棱柱棱长，长为该直四棱柱四倍底面边长，则长为：，宽为，面积为， ；（3）该直四棱柱的体积为，.16．如图所示是一个几何体的表面展开图．（1）该几何体的名称是______，其底面半径为______．（2）根据图中所给信息，求该几何体的侧面积和体积（结果保留m）【答案】（1）圆柱；1；（2）侧面积为；体积为．【解析】解：（1）该几何体的名称是圆柱，其底面半径为1，故答案为：圆柱；1；（2）该几何体的侧面积为：；该几何体的体积．17．如图，为了做一个无盖纸盒，小明先在一块矩形硬纸板的四角画出四个相同的正方形，用剪刀剪下．然后把纸板的四边沿虚线折起，并用胶带粘好，一个无盖纸盒就做成了．纸盒的底面是什么形状？为什么？【答案】矩形，它的四个角都是直角【解析】解：纸盒的底面是长方形形状，因为符合无盖长方体展开图的特征．