2022-2023年高中物理竞赛 功与能课件

这是一份2022-2023年高中物理竞赛 功与能课件，共40页。PPT课件主要包含了利用图象示功图，专题8-例1，示功图，当xnl时由，专题8-例2，由示功图得F力做的功，小试身手题2，摩擦力为线性变力，l-x0，小试身手题5等内容，欢迎下载使用。
利用图象求功之方法适用于当力对位移的关系为线性时;或在表示力对位移关系的F-s示功图中F(s)图线与s轴围成的图形“面积”有公式可依时;因为在F-s示功图中,这种“面积”的物理意义就是功的大小．
锤子打木桩,锤每次从同一高度落下,每次均有80%的能量传给木桩,且木桩所受阻力f与插入深度x成正比,试求木桩每次打入的深度比．若第一次打击使木桩插入了全长的1/3,全部插入须锤击多少次？
本题中的阻力f为一与位移x成正比的变力,即f=kx
图中各阴影“面积” 表示第1、2、3……次锤击中,木桩克服阻力做的功,数值上等于锤传给木桩的能量,设为W0．
某质点受到F=6x2的力的作用,从x=0处移到x=2.0 m处,试求力F做了多少功？
本题中的变力力F与位移x成F=6x2关系,F-x图线为抛物线
图中 “面积” 表示F力做的功
“面积” 由阿基米德公式
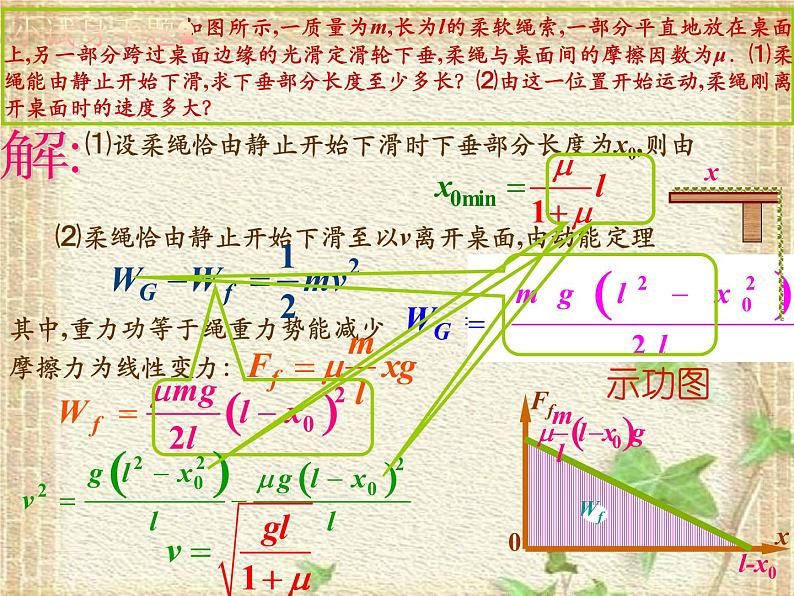
　　　　　 如图所示,一质量为m,长为l的柔软绳索,一部分平直地放在桌面上,另一部分跨过桌面边缘的光滑定滑轮下垂,柔绳与桌面间的摩擦因数为μ．⑴柔绳能由静止开始下滑,求下垂部分长度至少多长？⑵由这一位置开始运动,柔绳刚离开桌面时的速度多大？
⑴设柔绳恰由静止开始下滑时下垂部分长度为x0,则由
⑵柔绳恰由静止开始下滑至以v离开桌面,由动能定理
其中,重力功等于绳重力势能减少
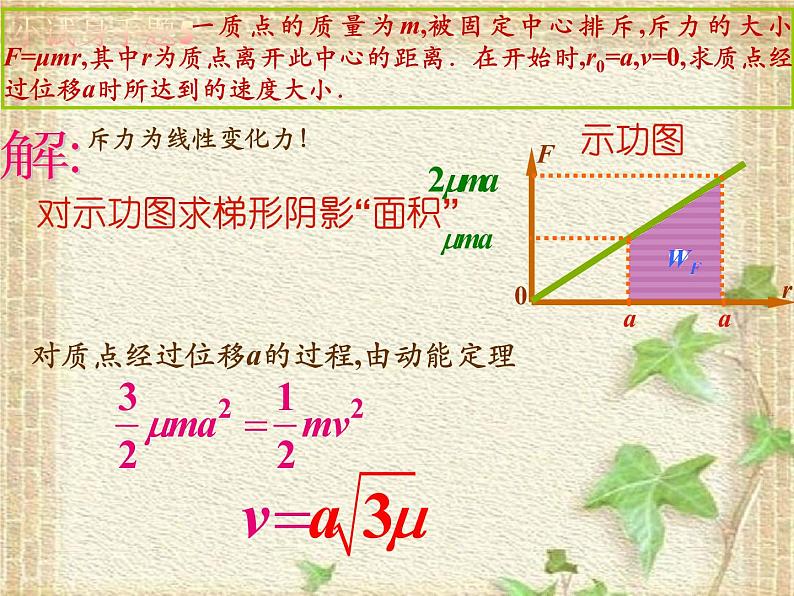
　　　　　 一质点的质量为m,被固定中心排斥,斥力的大小F=μmr,其中r为质点离开此中心的距离．在开始时,r0=a,v=0,求质点经过位移a时所达到的速度大小．
对示功图求梯形阴影“面积”
对质点经过位移a的过程,由动能定理
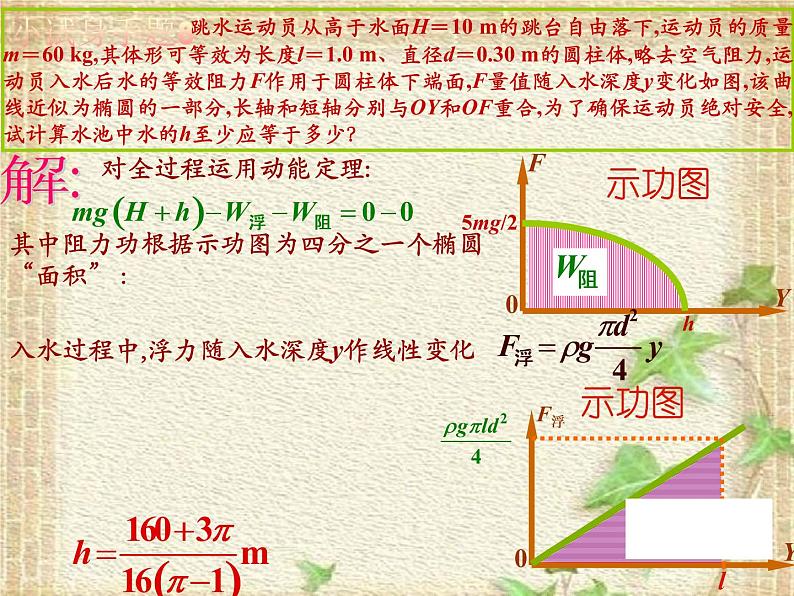
　　　　　 跳水运动员从高于水面H＝10 m的跳台自由落下,运动员的质量m＝60 kg,其体形可等效为长度l＝1.0 m、直径d＝0.30 m的圆柱体,略去空气阻力,运动员入水后水的等效阻力F作用于圆柱体下端面,F量值随入水深度y变化如图,该曲线近似为椭圆的一部分,长轴和短轴分别与OY和OF重合,为了确保运动员绝对安全,试计算水池中水的h至少应等于多少？
对全过程运用动能定理:
其中阻力功根据示功图为四分之一个椭圆“面积” :
入水过程中,浮力随入水深度y作线性变化
如果在某一位移区间,力随位移变化的关系为F=f(s) ,求该变力的功通常用微元法,即将位移区间分成n（n→∞）个小区间s/n,在每个小区间内将力视为恒定,求其元功Fi· s/n ,由于功是标量,具有“可加性”,那么总功等于每个小区间内元功之代数和的极限,即变力在这段位移中所做的功为：
在数学上,确定元功相当于给出数列通项式,求总功即求数列n项和当n→∞时的极限．
半径等于r的半球形水池,其中充满了水,把池内的水完全吸尽,至少要做多少功？
沿着容器的竖直直径,我们将水池内的水均匀细分成n层,每一元层水的高度
每一层水均可看作一个薄圆柱,水面下第i层水柱底面的半径
将这层水吸出至少应做的元功是
将池水吸尽至少要做的功是
一个质量为m的机动小车,以恒定速度v在半径为R的竖直圆轨道绕“死圈”运动．已知动摩擦因数为μ,问在小车从最低点运动到最高点过程中,摩擦力做了多少功？
小车沿竖直圆内轨匀速率运动到最高点的过程中,由于轨道支持力是变力,故而摩擦力为一随位置变化的力！
当小车运动在A处元圆弧段时
当小车运动在与A关于x轴对称的B处元圆弧段时
小车在关于水平直径对称的轨道两元段上摩擦力元功之和为
摩擦力在半圆周轨道上的总功
计算水平直径以下段摩擦力的功：
水平直径以上段摩擦力的功：
将板沿板长均分为n（n→∞）等份
　　　　　 将木板在水平地面上绕其一端转动角α,求所需要做的功．木板长度为L,质量为M,木板与地面之间的动摩擦因数为μ．
摩擦力对i段做的元功为
　　　　　 从一个容器里向外抽空气,直到压强为p．容器上有一小孔,用塞子塞着．现把塞子拔掉,问空气最初以多大速率冲进容器？设外界大气压强为p0,大气密度为ρ．
设小孔截面积为s,打开塞子后孔外侧厚度为Δx的一薄层空气在内、外压强差作用下冲入容器,获得速度v0,由动能定理:
这种求功方法依据功对能量变化的量度关系,只须了解初、未能量状态,得到能量的增量便是相应的功量．
如图所示,一质量分布均匀的粗绳长2a,质量为2m,两端悬于水平天花板上相距为a的两点而悬垂静止,其重心位于天花板下方b处.现施一力于绳之最低点C并将绳拉直至D点,求拉力所做的功．
由几何关系拉直后两段绳的重心位置距天花
由于拉力做功,使绳之重心高度变化因而重力势能变化,重力势能的增量即为所求拉力功量．
一质量为m的皮球,从高为h处自由下落（不计空气阻力）,反弹起来的高度为原来的3/4,要皮球反弹回h高处,求每次拍球需对球做的功
在球与地面接触期间,地面对球的弹力对球做负功,使球的动能减少．地面对球的弹力功是变力功!
牛顿碰撞定律：若两球碰撞前速度依次为v10、v20,碰撞后速度为v1、v2,则碰撞后两者的分离速度v2－ v1与碰撞前两者的接近速度v20－ v10成正比,比值e称恢复系数（或反弹系数）,比值由两者的质料决定,即
从h高度自由下落再反弹的全过程,地面弹力功W1:
从h高度拍下再反弹原高的全过程,地面弹力功W2:
从h高下落未速度即与地接近速度:
从地面反弹的起跳速度即与地分离速度:
同一球与同一地面碰撞,恢复系数相同:
　　　　　 如图所示,有两个薄壁圆筒．半径为R的圆筒绕自己的轴以角速度ω转动,而另一个圆筒静止．使两圆筒相接触并且它们的转轴平行,过一会儿,由于摩擦两圆筒开始做无滑动的转动．问有多少机械能转换成内能？（两圆筒的质量分别为m1、m2）
根据题意,一段时间内m1线速度从ωR→ ω1R,而m2线速度从0 → ω2r= ω1R
这种变化是因为两者间有大小相等的一对力作用,这对力做功使系统机械能(动能)转换成内能 !
又,由牛顿第二、三定律,一对力大小相等:
功是力的空间积累作用,能是对物体运动的一种量度．功的作用效应是使物体的能量状态发生变化,做功的过程就是物体能量转化的过程,转化了的能量都可以由做功的多少来量度,这是我们对功与能之间关系的基本认识,是我们从能量角度解决运动问题的依据．
借助功与能的具体对应关系,对运动的功的量度问题作出正确的操作.
⑵确定有哪些力对研究对象做了正功或负功,以代数和的形式完成定理中等号左边对合外力的功的表述；
⑶分析所研究过程的初、未两状态的动能,完成等号右边对动能变化的表述 ；
⑴选定研究的对象与过程;
一定的能量变化由相应的功来量度
※重力功量度重力势能的变化：
※外力（可以是重力、弹力、摩擦力、电场力、磁场力或其它力）做的总功量度动能的变化：
※弹力功量度弹性势能的变化：
※引力功量度引力势能的变化：
※非重力弹力功量度机械能的变化：
※电场力功量度电势能的变化：
（W非可以是摩擦力功、电场力功、安培力功或其它非重力、弹簧弹力的功）
如图示,一水塔的蓄水箱底离地面的高度H0=20 m,其横断面是半径R=2 m的圆．储水深h=1 m,如果用装在高H1=5 m处、截面积为2 cm2的水龙头放水,问需要多久才能将水放完？
根据题意,水箱中的水从底部截面积为s的小孔流出,若流速为vi,则时间ti内的水流量Qi= vi ti S；总储水全部流尽的时间应为
每层水放出时间的通项式为
全部水箱储水放尽的总需时为
设小孔处一小片厚Δx、面积S的液片,在内外压力之合力作用下获得速度v而离开小孔,由动能定理:
质量为m的小球以某一初速度竖直上抛,若运动中所受阻力Ff=kv2,最大阻力为重力的0.44倍,试求小球上升的最大高度H及落回抛出点时的速度vt．
本题通过元过程的动能定理,用微元法求得终解!
本题研究过程中有重力功与阻力功,其中阻力功为耗散功,且为一按指数规律变化的力!
取上升过程中的某一元过程：该过程小球上升了高度H/n(n→ ∞),速度从vi减少为vi+1,各元过程中的阻力可视为不变为
根据动能定理,对该元过程有
在各相同的上升高度H/n微元中,合外力大小成等比数列递减、因而动能的增量是成等比数列递减的,其公比为
对此式两边取n次方当n→∞极限:
小球落回抛出点时的速度是抛出时速度的六分之五
一质点在光滑的固定半球面上距球心高度为H的任意点P,在重力作用下由静止开始往下滑,从Q点离开球面,求PQ两点的高度差h．
本题除重力外无非保守力的功,机械能守恒!
设球半径为R
若质点从球顶部无初速滑下,则可沿球面滑下R/3的高度,释放高度H越小,沿球面滑下的高度越短．这是一个有趣又有用的模型．
⑴在如示坐标中分解力F
在与F垂直方向上线对钢球的力大小为
⑵设钢球第一次碰撞时沿F方向速度为vx,垂直于F方向速度为vy,设力F的位移为x,由动能定理
⑶达到终态时,两球vy=0,F总位移X,有
设抵达墙时战士速度为v,蹬墙后速度为v′,各矢量间关系如示,
从起跳至上升至最高H处,由机械能守恒:
　　　　　 质量为M、长为l的板放在冰面上,在板的一端坐着质量为m的小猫它要跳到板的另一端,问小猫对冰面的最小速度v0min应为多少？小猫为使跳到板的另一端所消耗的能量最少, 问它的初速度v0应该与水平面成多大角α？
猫消耗能量E,使猫及木板获得初动能：
起跳时间Δt内m与M间水平方向相互作用力大小相等,故有
猫从跳离板一端到落至板另一端历时由竖直方向分运动得
这段时间内猫对板的位移应满足
利用基本不等式性质 ：
⑴由机械能守恒,棒第一次碰地以前速度
棒与地相碰后瞬时速度大小不变、方向向上,
从棒从地面向上到与环相对静止的过程中,一对摩擦力做负功,重力分别对环、棒做负功,由动能定理：
⑵棒与环一起以V1自由下落h至第二次落地时速度仍由机械能守恒
则若在碰n次后环脱离棒,n、k、L、H四个量应满足的关系：
　　　　　 钢球沿着光滑的长梯弹跳,在每一级台阶上仅跳一次,如图所示．每次与台阶碰撞时,球要损失η＝50％的机械能．试求小球抛出时的初速度v及其与竖直线的夹角φ．（梯子台阶的高度h＝10cm,宽l＝20cm）
根据题意,第一次与平台碰撞前后有
每次跳起到落到下一台阶的过程中,有
由水平方向的匀速运动得钢球每一次飞行时间
说明起跳速度变为水平,除钢球落在拐点情况外,应舍去此解
取元功作微元,以功能原理为基本依据求得一类物理问题解答的方法,我们称之为“元功法”.这种解法所循基本原理是分析力学中的“虚功原理”,由伯努利首先提出的．用元功法可以处理某些平衡问题,且颇为简单．
取与原平衡状态逼近的另一平衡状态,从而虚设一个元过程,此过程中所有元功之和为零,以此为基本关系列出方程,通过极限处理,求得终解．
如图所示,质量为m、长度为l的均匀柔软粗绳,穿过半径R的滑轮,绳的两端吊在天花板上的两个钉子上,两钩间距离为2R,滑轮轴上挂一重物,重物与滑轮总质量为M,且相互间无摩擦,求绳上最低点C处的张力．
分析粗绳、滑轮和重物构成的系统的受力情况
分析绳之一半的受力情况
设想在A处以力TA将ABC段绳竖直向上拉过一极小距离Δx
如图示,一轻三足支架每边长度均为l,每边与竖直线成同一角度,三足置于一光滑水平面上,且恒成一正三角形,现用一绳圈套在三足支架的三足上,使其不能改变与竖直线间的夹角,设三足支架负重为G,试求绳中张力FT．
设想支架各边足部在绳合力作用下向正三角形中心移动一极小位移 Δx:
支架每个足部绳合力元功
Δx与Δy几何关系如示 :
当Δx→0, Δθ →0,
　　　　　 如图,所示的曲柄连杆机构中,设曲柄端A上所受的竖直力为Q,由活塞D上所受的水平力P维持平衡,试用元功法求P与Q的比值．图中α、β为已知．
设想设活塞D（即连杆的B端）以速度v通过一微小位移Δx,与此同时,连杆A端以速度vA绕C点通过一小段弧
vA 与v杆约束相关关系如示
vA方向与曲柄CA垂直,且是与B相同的水平速度v及对B点的转动速度vn的矢量和
在力P发生水平位移Δx的时间内,力Q发生的竖直位移为
　　　　　 如图所示,均匀杆OA重G1,能在竖直面内绕固定轴O转动,此杆的A端用铰链连住另一重G2的均匀杆AB,在AB杆的B端施一水平力F,试用元功法求二杆平衡时各杆与水平所成的角度α及β．
设想水平力使AB杆的B端移动极小位移Δx3
同时,G1、G2力沿力方向的极小位移各为：