2022-2023年高中物理竞赛 机械振动二三事课件

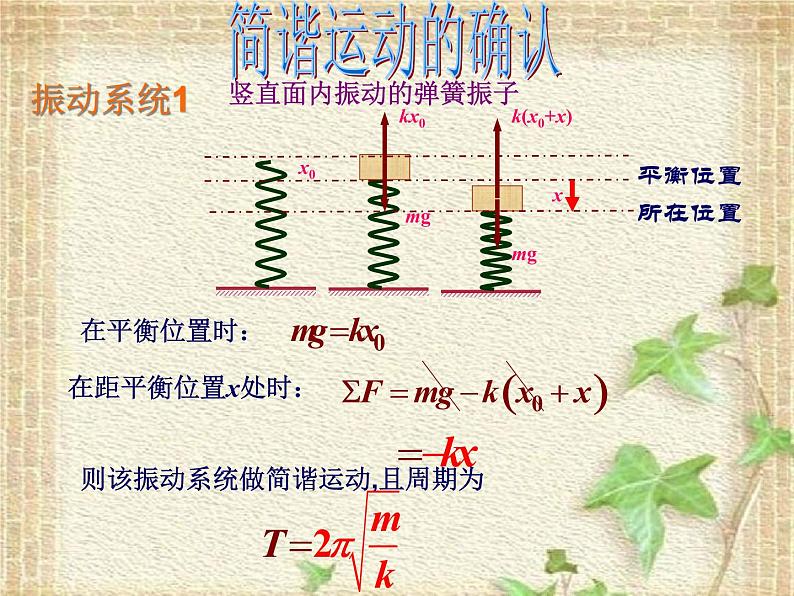
这是一份2022-2023年高中物理竞赛 机械振动二三事课件，共54页。PPT课件主要包含了平衡位置，所在位置，在平衡位置时，在距平衡位置x处时，简谐运动的确认，振动系统1，当θ角很小时，振动系统2，振动系统3，该液片在平衡位置时等内容，欢迎下载使用。
则该振动系统做简谐运动,且周期为
竖直面内振动的弹簧振子
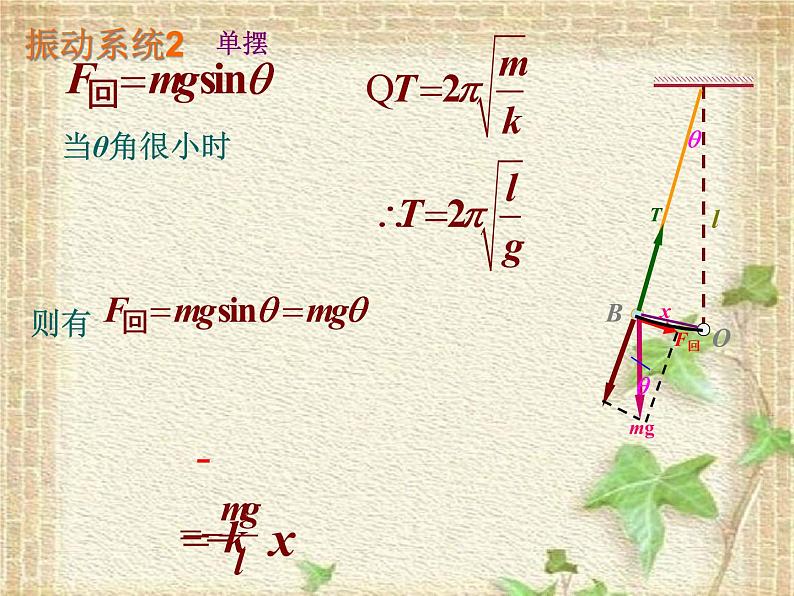
单摆
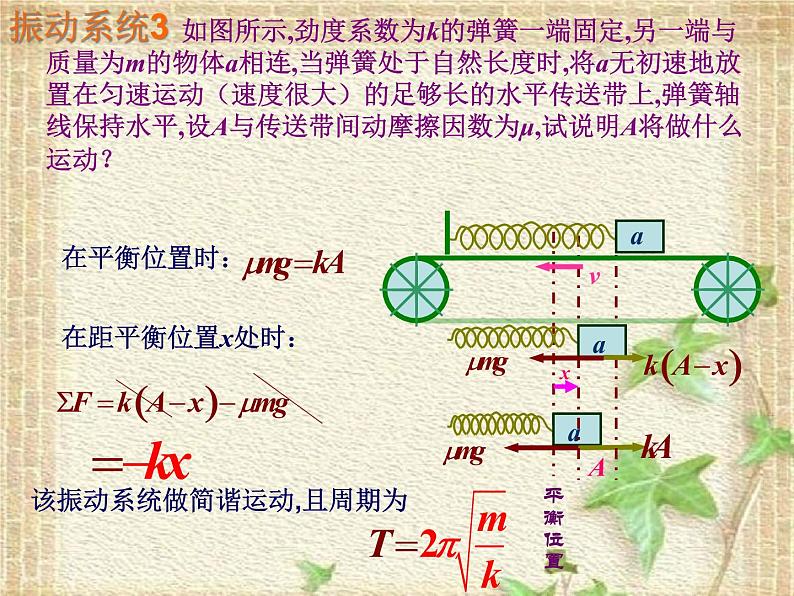
如图所示,劲度系数为k的弹簧一端固定,另一端与质量为m的物体a相连,当弹簧处于自然长度时,将a无初速地放置在匀速运动（速度很大）的足够长的水平传送带上,弹簧轴线保持水平,设A与传送带间动摩擦因数为μ,试说明A将做什么运动？
该振动系统做简谐运动,且周期为
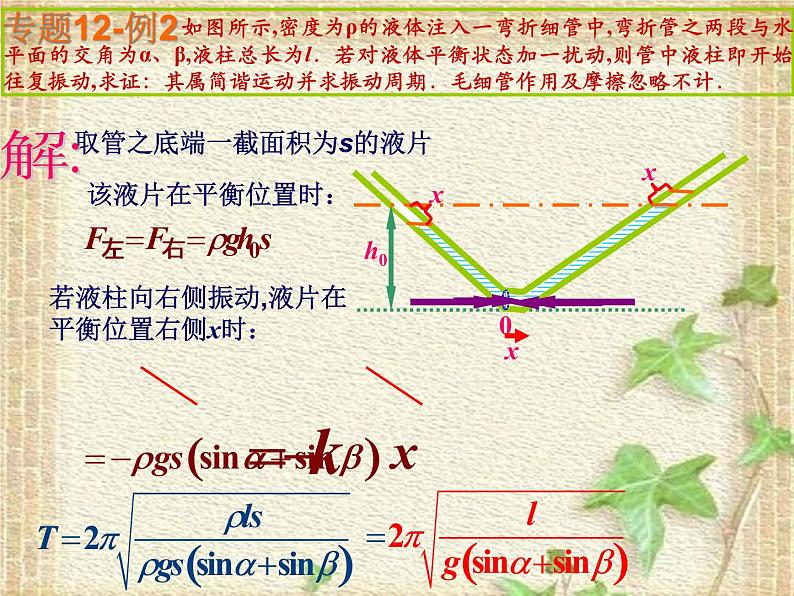
　　　　　 如图所示,密度为ρ的液体注入一弯折细管中,弯折管之两段与水平面的交角为α、β,液柱总长为l．若对液体平衡状态加一扰动,则管中液柱即开始往复振动,求证：其属简谐运动并求振动周期．毛细管作用及摩擦忽略不计．
取管之底端一截面积为s的液片
若液柱向右侧振动,液片在平衡位置右侧x时：
可知小球在隧道中做简谐运动!
小球过平衡位置时速度最大,为:
　　　　　 如图所示,设想在地球表面的A、B两地之间开凿一直通隧道,在A处放置一小球,小球在地球引力的作用下从静止开始在隧道内运动,忽略一切摩擦阻力．试求小球的最大速度,以及小球从A到B所需时间．已知地球半径为R,地球表面的重力加速度为g,A和B之间的直线距离为L,地球内部质量密度设为均匀,不考虑地球自转．
质点在距平衡位置x的某位置时：
　　　　　 力心A、B相距l,一质量为m的质点受与距离平方反比的有心斥力作用而平衡于两点连线上的O点,若将质点稍稍偏离平衡位置,试确定其运动情况．
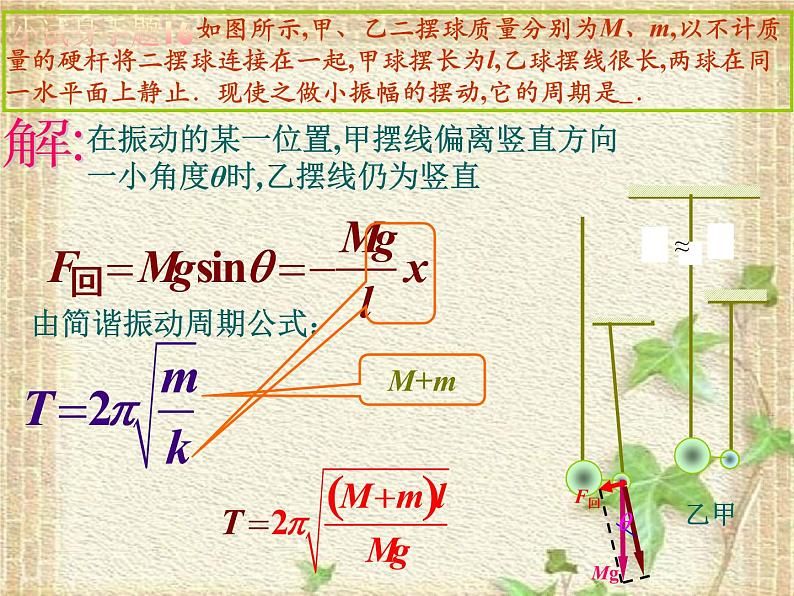
在振动的某一位置,甲摆线偏离竖直方向一小角度θ时,乙摆线仍为竖直
如图所示,甲、乙二摆球质量分别为M、m,以不计质量的硬杆将二摆球连接在一起,甲球摆长为l,乙球摆线很长,两球在同一水平面上静止．现使之做小振幅的摆动,它的周期是 ．
框架处于静止 ,受力如图:
三根长度均为l＝2.00 m,质量均匀的直杆,构成一正三角形框架ABC,Ｃ点悬挂在一光滑水平转轴上,整个框架可绕转轴转动,杆AB是一导轨,一电动玩具松鼠可在导轨上运动,如图所示．现观察到松鼠正在导轨上运动而框架却静止不动,试论证松鼠的运动是一种什么样的运动并作描述．
当重物位置在距铰接点l时 ,系统处于平衡时,若弹簧形变量为x0受力如图:
振动中重物有一对平衡位置位移x时,重物受力如图:
长度为Ｌ的轻铁杆,一端固定在理想的铰链上,另一端搁在劲度系数为k的弹簧上,如图．试确定铁杆小振动周期与质量为m的重物在杆上的位置之关系．
木板处于平衡位置时,受力如图
若木板有一位移-重心向右轮移过x时
如图,质量为m 的均匀长木板水平地置于两个匀速反向转动的轮上．设轮与木板间摩擦因数为μ,两轮间距离l,平衡时长木板重心在l/2处．若将木板稍稍拉过一小段后放手,则木板将在轮上做往复振动,这种振动是简谐运动吗？若是,求其周期．
⑴若左轮不光滑且顺时针转动,
设再向右有一小位移x时
如图,质量为m的均匀木板对称地放在两个滚柱上,两滚柱轴线间的距离为l,其中一个滚柱和板之间摩擦因数为μ,而在另一个滚柱上,板可无摩擦地滑动．用一劲度系数为k的弹簧将板连接在竖直墙壁上,当板处于平衡位置时,使不光滑的滚柱快速旋转起来．问摩擦因数μ为多大,木板相对平衡位置有了位移后可做简谐运动？振动的圆频率是多少？
⑵若左轮不光滑且逆时针转动,
设再向左有一小位移x时
右轮不光滑且逆时针转动同⑴
右轮不光滑且顺时针转动同⑵
质点P以角速度ω沿半径为R的圆轨道做匀速圆周运动,试证明：质点P 在某直径上的投影的运动为简谐运动．
P的投影运动所受回复力Fx
∴简谐运动的周期公式为
根据题给条件,物体振动方程为
质量为10 g的物体做简谐运动,振幅为24 cm,周期为4 s；当t＝０时坐标为+24 cm.试求⑴当t＝0.5 s时物体的位置．⑵当t＝0.5 s时作用在物体上力的大小和方向．⑶物体从初位置到x＝-12 cm处所需的最短时间．⑷当x＝－12 cm时物体的速度．
⑴作如图所示谐振参考圆,由图得
⑶路程末端小物体回复力由最大静摩擦力提供：
一物体在水平面上做简谐运动,振幅为10 cm,当物体离开平衡位置6 cm 时,速度为24 cm/s．⑴问周期是多少？⑵当速度为±12 cm/s时,位移是多少？⑶如果在振动的物体上加一小物体,当运动到路程的末端时,小物体相对于物块刚要开始滑动,求它们之间的摩擦因数？
⑴确定摆球振动的平衡位置；⑵确定摆在此位置时摆线上的力FT；⑶等效的重力加速度
由理想单摆周期公式
,通常可由三条途径确定T：
．★确定等效悬点及摆长
⑴联结两悬点的直线为转轴；⑵摆球所受重力作用线反向延长与转轴交点为首选等效悬点；⑶取首选等效悬点与摆球间的距离为等效摆长
★确定等效的重力加速度
⑴确定摆球振动中的机械能守恒关系⑵比对异形摆的能量关系式与标准单摆的能量关系式⑶在同一参考圆下提取等效的角速度
若单摆在加速度竖直向上的电梯中做小幅振动,在振动的“平衡位置”
若单摆在加速度水平向左的车厢中做小幅振动,
带正电摆球在水平向右的电场中做小幅振动
如图所示,摆线长为l的单摆悬于架上,架固定于小车．使小车沿倾角为的斜面以加速度a做匀加速运动,求此时单摆振动的周期．
某栋高层大楼的电梯服务员是位一丝不苟的人,他为按时结束一天的工作,把一台准确的摆钟挂在电梯的壁上．电梯向上加速和向下加速的时间相同,加速度大小也相同．试问电梯服务员是按时结束工作,还是超时或提早了呢？
向上加速的电梯中,摆的等效
而加速下降电梯中,摆的等效
因加速,上升过程钟面时间t比客观时间t0长,
下降过程钟面时间t比客观时间t0少,
每上下一次,钟面读数与客观时间相差
说明每上下一次,钟面指示时间比实际时间少,以此钟指示时间为据此人 工作了．
不准钟当其钟面读数时间为t时,客观时间为t0． t＞t0,钟走快； t＜t0,钟走慢．
摆式钟的特点　 1.振动次数相同,则钟面读数变化相同　　　　　　　 2.标准钟钟面读数与客观时间一致 不准钟钟面读数与客观时间不一致　　　　　　　 3.T大钟慢,T小钟快
设标准钟摆的周期为T0,不准钟摆的周期为T．如图,当两钟从同一初始读数开始走时,分别出现读数t时
标准钟是在与钟面读数一致的时间t内走成这样的：
不准钟是在客观时间t0(t0≠t)内走成这样的：
如图,小铁球用长度为l的细线AC、BC悬挂,两线与A、B连线的夹角均为α,AC恰好水平．球由于受到扰动,垂直于纸面向外略微偏离平衡位置,然后小球来回振动,求小球振动的周期．
如图所示, 光滑的细杆组成夹角为α的人字架．一根长度为l的轻线套在架子上,线的两端共系一个重球C,架竖直放置,试求重球在人字架平面内做小振动的周期．
振动是在线拉力与重力之合力作用下发生的,若证得振动中线拉力之合力始终通过O点,即可与单摆等效!
由几何关系得C到AB的距离
如图所示,秋千的一根绳子的固定点A比另一根绳固定点B高b,秋千两根支架相距为a,两根绳子长度分别是l1和l2,并且 ．试求人坐在这样的秋千上小摇荡的周期．（人的大小与上述长度相比可忽略不计）
一端带有重物的轻硬杆,另一端用铰链固定在墙上A点,杆可以向各个方向转动,如图所示．一根长度为l的不可伸长的线沿竖直方向系在杆的中点,以保持杆处于水平位置．使重物具有垂直图面方向的动量,试求系统小振动的周期 T．
如图是一种记录地震的仪器——倾斜摆的示意图.摆球m固定在边长为l、质量可忽略的等边三角形框架ABC上,可绕AB杆摆动,AB杆和竖直墙夹角为α.求摆球做微小摆动的周期.
未放凹形滑块的单摆,是以圆频率
设带凹形滑块的异形摆圆频率为
如图,摆球质量为m,凹形滑块质量为M,摆长为l．m与M、M与水平面之间光滑,令摆线偏转很小角度后,从静止释放,求系统的振动周期T．
未加另一质量重物的单摆
设带另一质量的复摆圆频率为
一个单摆,由一根刚性轻杆和杆端的重物组成,做小振幅的自由振动．如果在杆上某点再固定一个和杆端重物质量相同的重物,使原单摆变成一个异形复摆,其振动周期最多改变百分之几？
在天花板下用两根长度同为l的轻绳吊一质量为M的光滑匀质木板,板中央有一质量为m的小滑块,如图．开始时系统静止,然后使板有一个水平的横向小速度v0,试求振动周期．
摆长为l、振幅为lθ的理想单摆满足
对振动实体机械能守恒,有
数学摆是由长度为l的轻杆,一个固定在杆的自由端上的小铅球所组成．现在,在杆上套一粒同铅球质量相等的珍珠,它可以沿着杆中点的水平线自由地滑动,如图所示．试求这种摆小振动的周期,摩擦不计．
摆长为l、振幅为lθ 的理想单摆满足
此题中复摆振动实体机械能守恒,有
如图所示,质量为M、长为L的均匀细刚杆一端悬挂,可在竖直平面内绕悬点O无摩擦地摆动．质量为m=M/3的小虫相对杆以速度v缓慢地沿杆向下爬行．开始时,杆静止并与竖直线成一个小角度θ0,小虫位于杆上端悬点处．释放杆,杆开始摆动,小虫开始爬行,试求⑴小虫沿杆爬行l距离时,杆振动的圆频率；⑵小虫爬行到杆下端时,系统的能量减为初时的 ,求杆的摆动幅度θt．
确定绕杆一端以角速度转动的均匀细杆的动能,如图
⑴当小虫爬到距悬点l处时,虫与杆构成的振动系统能量关系为
对A=Lθ 的理想单摆满足
摆长为l、振幅为lφ的理想单摆满足
其中角速度为ω、半径为r圆板的动能为
如图所示,一质量为m、半径为r的圆板用三根长均为l的细线悬于天花板上,连接点恰好三等分圆板的圆周,若圆板绕其过中心O的铅直轴做微小转动,试求其周期．
如图所示,细轴环用铰链固定于A点,开始这样放置轴环,使它的质心位于A点正上方,此后轴环自由下落,经时间τ＝0.5 s,轴环的质心处于最低位置．有一摆是小重球B固定在轻硬杆上,杆的长度等于轴环的半径,如果开始小球处于最高位置并自由落下．试问此摆经过多少时间t返回到下面的平衡位置．
比较两者的角速度关系：
如图所示,半径为R的细圆环,其质量与固定在其上的两个相同小重物相比可忽略不计．在环上与两小重物等距处钻个孔,将孔穿过墙壁上的钉子而把环悬挂起来,使环可以在竖直平面内无能量损失地做微小简谐振动（象摆一样）．两小重物的位置关系可以用它们之间的角距离2α表征．试求该摆的振动周期T及其随变化的图线．
系统从平衡位置偏离最大幅度为角θ：
摆长为l、振幅为A的理想单摆满足
如图所示,质量为M的小平板固定在劲度系数为k的轻弹簧上,弹簧的另一端固定在地上,有一质量为m的小球沿入射角θ方向以速度v0射向小平板,并发生完全弹性碰撞．忽略一切摩擦,求碰撞后小平板的振动方程．
车与缓冲器一起自由振动过程是谐振过程,其中
平衡位置时的压缩量为:
振幅由振动能量关系求得:
如图所示,小车质量M＝4 kg,由静止开始沿倾角的斜面自h=5 m高处滑下,与一弹簧缓冲器相碰而自由振动,然后又冲上斜面．若缓冲器弹簧的劲度系数k=100 N/m．求缓冲器弹簧的最大压缩量及小车被缓冲的时间．
如图所示,在盛密度为的液体的大容器中放入一只底面积为S的小圆柱形容器,在这个容器的底部又插入一根细导流管．两只容器壁均静止不动,在小的容器中注入密度为（ρ2＞ρ1）的染了颜色的液体,使其高度至H ,以使与外面容器的液面相平．然后打开细管上端,可以看到重液通过细管流入大容器并沉入底部,但经过一段时间轻液开始进入小容器中,以后这个过程重复地进行着．如果假设液体不会混合且表面张力不计,试求第一次从小容器里流出的重液的质量Δm1是多少？在以后每次循环中,流进小容器的轻液的质量Δmn和从小容器里流出的重液的质量Δmk各是多少？
设小容器底部开口与细管相接部截面积为s,从此处流过的小液片恰受力平衡时,重液液面下降x0,若称此为平衡面,则有
在此前（后）液面高（低）于平衡面x时,对应地正流经细管上口的小液片所受合力为
即:小液片以谐振形式从开口流出,当重液面下降2x0时,重液片向下速度减为零,此后将换成轻液片上升．故第1次从小容器中流出的重液质量为
此后将换成轻液片上升,静止于重液上层,当细管口轻液片受力平衡时,小容器内下部是高(H-2x0)的重液,上部轻液高度设为
即:轻液片亦以谐振形式从开口流入,当轻液面上升2x0时,轻液片向上速度减为零,此后将换成重液片下降．故第2次流入小容器的轻液质量为
每次循环中进出小容器的重液与轻液质量相同,直至小容器中重液全部替换成轻液!
如图所示,平台A的质量为m,由劲度系数为k的轻弹簧来支持．弹簧上端与A相连,下端与地面相连,物块B的质量也是m,自由地放在平台中心,现用竖直向下的力F=mg把弹簧压下（仍在弹性限度内）,并在系统静止时撤去外力,求此后A、B的运动情况及两者各自到达的最大高度．
A、B处于平衡位置时弹簧压缩
A、B一起振动的运动方程
A、B一起振动至弹簧自然伸长时速度为
A、B在此位置分离,B竖直上抛到达最大高度
A继续上升可达最大高度为
A返回分离位置处历时一周期
由于A、B分离后经相同时间回到分离处,故对碰而交换速度,再经
A、B同速相遇一起向下做参数为A、ω及初相为
的谐振,至向上过初始位置
整个过程中B到达的最高点距释放点
整个过程中A到达的最高点距释放点
两系统以2v速度接近,经时间
相碰撞的两物体交换速度!
碰撞后瞬时系统情况如图:
两系统各做简谐振动,经半周期发生第二次碰撞:
相碰撞的两物体再次交换速度!
两系统以2v速度分离经
如图所示,两个系统,每个都是由两个质量均为m的相同物体组成,两物体间用劲度系数为k的弹簧相连．两系统以大小相同的恒定速度v相向运动．某时刻,将相碰的两物体间距离L．问经过多少时间后,这两物体间的距离又等于L？设碰撞是完全弹性的．
振动能转变为热及向四周辐射!
如图所示 实验装置可以测定液体的粘滞系数：在弹簧上悬挂一薄板A,测定它在空气中的周期T0,然后把薄板放在欲测粘滞系数的液体中,令其振动,测定周期T．已知薄板质量为m,表面积为S,液体的粘滞阻力 ,v为运动速度．确定液体的粘滞系数．