数学八年级上册1 探索勾股定理课文内容ppt课件

这是一份数学八年级上册1 探索勾股定理课文内容ppt课件，共23页。PPT课件主要包含了探索勾股定理，Contents，情境导入，巩固练习，课堂小结，新知探究，作业布置，测量法，数学小史，2符号语言等内容，欢迎下载使用。

2002年世界数学家大会在我国北京召开，下图是数学家大会的会标。会标中央的图案是赵爽弦图，它与“勾股定理”有关。
科学家曾经建议用“勾股定理”的图来作为与“外星人”联系的信号。古希腊的毕达哥拉斯学派首先证明了这个关系。
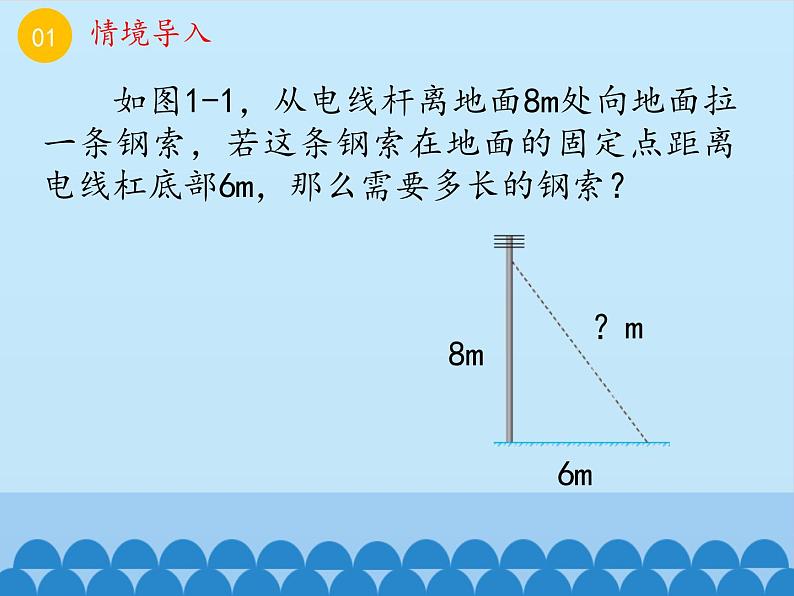
如图1-1，从电线杆离地面8m处向地面拉一条钢索，若这条钢索在地面的固定点距离电线杠底部6m，那么需要多长的钢索？
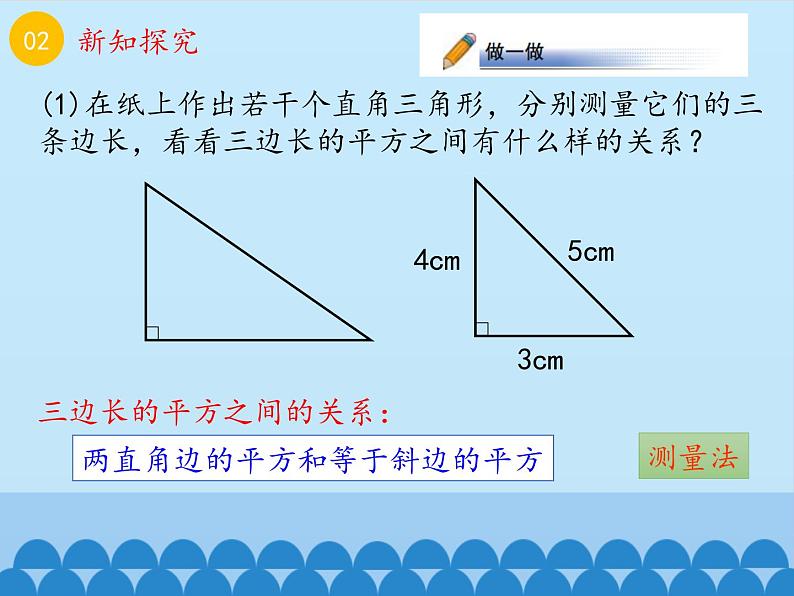
(1)在纸上作出若干个直角三角形，分别测量它们的三条边长，看看三边长的平方之间有什么样的关系？
两直角边的平方和等于斜边的平方
三边长的平方之间的关系：
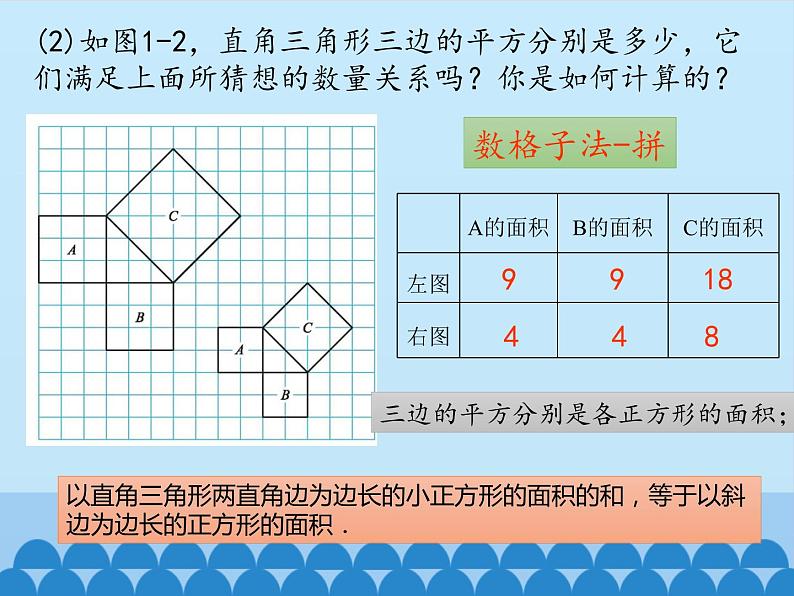
(2)如图1-2，直角三角形三边的平方分别是多少，它们满足上面所猜想的数量关系吗？你是如何计算的？
三边的平方分别是各正方形的面积；
9 9 18
4 4 8
以直角三角形两直角边为边长的小正方形的面积的和，等于以斜边为边长的正方形的面积．
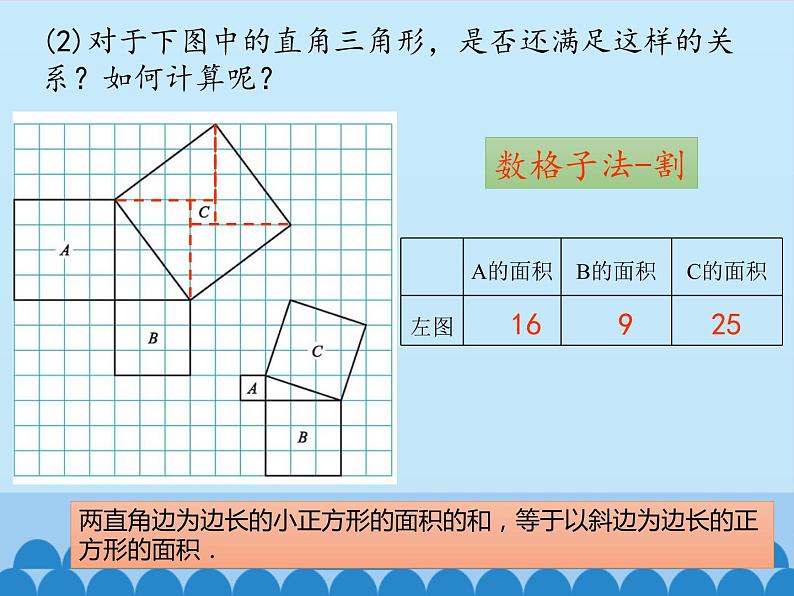
(2)对于下图中的直角三角形，是否还满足这样的关系？如何计算呢？
16 9 25
两直角边为边长的小正方形的面积的和，等于以斜边为边长的正方形的面积．
(2)对于下图中的直角三角形，是否还满足这样的关系？你又是如何计算的呢？
ⅱ.满足“两直角边的平方和等于斜边的平方”。
1 9 10
(3)如果直角三角形的两直角边分别为1.6个单位长度和2.4个单位长度，上面所猜想的数量关系还成立吗？
直角三角形，勾股定理成立，斜边长约为2.9（1.62+2.42=2.92 ）。
我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦，“勾股定理”因此而得名.（在西方文献中称为毕达哥拉斯定理）
(1)文字语言：直角三角形两直角边的平方和等于斜边的平方。
如图，从电线杆离地面8m处向地面拉一条钢索，若这条钢索在地面的固定点距离电线杠底部6m，那么需要多长的钢索？
已知直角三角形两边，求第三边。
1.求下图中字母所代表的正方形的面积：
225+400=625152+202=252
225-81=14492+122=152
2.小明妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后，发现屏幕只有58厘米长和46厘米宽，他觉得一定是售货员搞错了。你同意他的想法吗？
462+582=2116+3364=5480742=5476
1.求下列直角三角形未知边的长度：
2.求斜边长17厘米、一条直角边长15厘米的直角三角形的面积。
172-152=289-225=64=82
直角三角形的两条直角边为8，15
S直角三角形=8×15×1/2=60
3.如图，所有的四边形都是正方形，所有的三角形都是直角三角形，请在图中找出若干个图形，使它们的面积之和恰好等于最大的正方形面积，尝试给出两种以上的方案。
方案2：A+B+F=G
方案3：A+B+C+D=G
方案4：E+C+D=G
4.如图，求等腰△ABC的面积。
解： △ABC为等腰三角形，作BC边上的高AD，
则AD⊥BC,BD=DC=3
AD2=AB2-BD2=25-9=16
S△ABC=BC×AD×1/2=6×4×1/2=12
2.验证“勾股定理”的方法：
(2)数格子法（拼、割、补）
3.“勾股定理”的应用：