辽宁省2022年中考数学卷真题分题型分层汇编-04选择题（中档题）

这是一份辽宁省2022年中考数学卷真题分题型分层汇编-04选择题（中档题），共22页。
辽宁省2022年中考数学卷真题分题型分层汇编-04选择题（中档题）
一．实数大小比较（共1小题）
1．（2022•营口）在，0，﹣1，2这四个实数中，最大的数是（　　）
A．0 B．﹣1 C．2 D．
二．同底数幂的除法（共1小题）
2．（2022•辽宁）下列运算正确的是（　　）
A．（a2）4＝a6 B．a2•a4＝a6 C．a2+a4＝a6 D．a2÷a4＝a6
三．单项式乘单项式（共1小题）
3．（2022•辽宁）下列运算正确的是（　　）
A．2a2•3a＝6a3 B．（2a）3＝2a3
C．a6÷a2＝a3 D．3a2+2a3＝5a5
四．由实际问题抽象出二元一次方程组（共1小题）
4．（2022•盘锦）《九章算术》是中国传统数学重要的著作，奠定了中国传统数学的基本框架．其中《盈不足》卷记载了一道有趣的数学问题：“今有共买物，人出八，赢三；人出七，不足四．问人数、物价各几何？”译文：“今有人合伙购物，每人出8钱，会多出3钱；每人出7钱，又差4钱．问人数、物价各多少？”设人数为x人，物价为y钱，根据题意，下面所列方程组正确的是（　　）

A． B．
C． D．
五．根的判别式（共2小题）
5．（2022•辽宁）下列一元二次方程无实数根的是（　　）
A．x2+x﹣2＝0 B．x2﹣2x＝0 C．x2+x+5＝0 D．x2﹣2x+1＝0
6．（2022•营口）关于x的一元二次方程x2+4x﹣m＝0有两个实数根，则实数m的取值范围为（　　）
A．m＜4 B．m＞﹣4 C．m≤4 D．m≥﹣4
六．解分式方程（共1小题）
7．（2022•营口）分式方程＝的解是（　　）
A．x＝2 B．x＝﹣6 C．x＝6 D．x＝﹣2
七．动点问题的函数图象（共2小题）
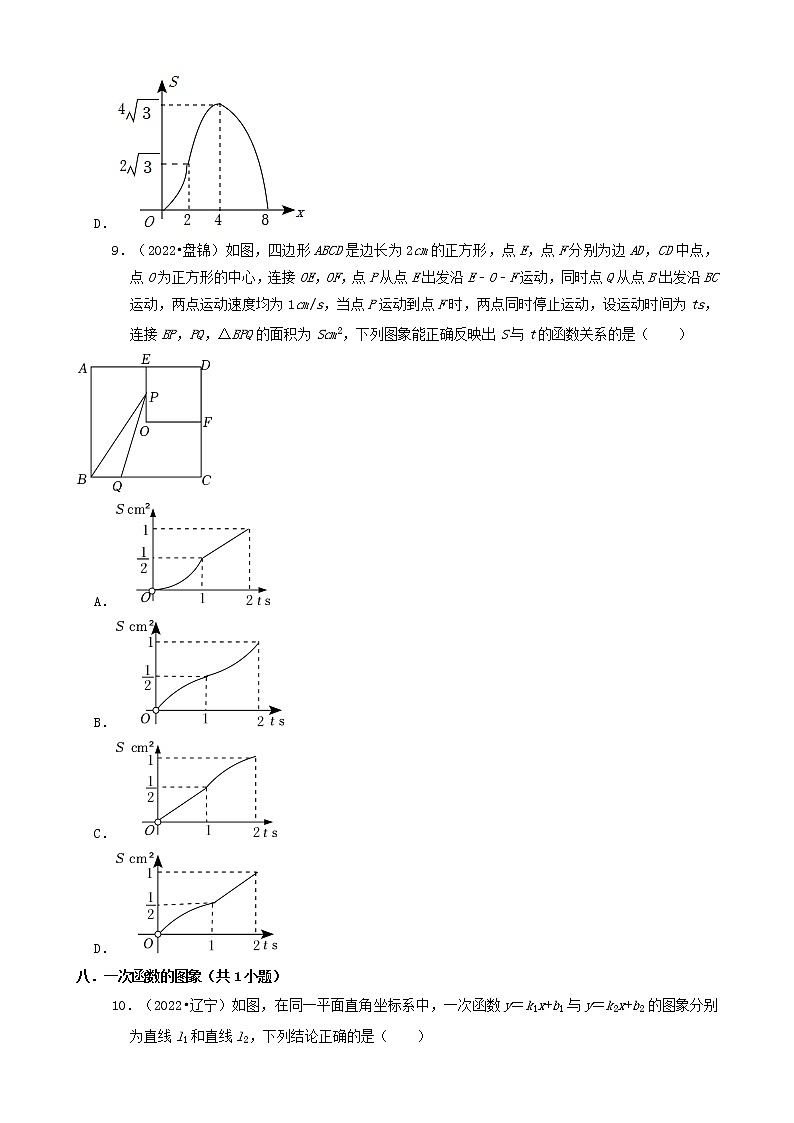
8．（2022•辽宁）如图，在等边三角形ABC中，BC＝4，在Rt△DEF中，∠EDF＝90°，∠F＝30°，DE＝4，点B，C，D，E在一条直线上，点C，D重合，△ABC沿射线DE方向运动，当点B与点E重合时停止运动．设△ABC运动的路程为x，△ABC与Rt△DEF重叠部分的面积为S，则能反映S与x之间函数关系的图象是（　　）

A．
B．
C．
D．
9．（2022•盘锦）如图，四边形ABCD是边长为2cm的正方形，点E，点F分别为边AD，CD中点，点O为正方形的中心，连接OE，OF，点P从点E出发沿E﹣O﹣F运动，同时点Q从点B出发沿BC运动，两点运动速度均为1cm/s，当点P运动到点F时，两点同时停止运动，设运动时间为ts，连接BP，PQ，△BPQ的面积为Scm2，下列图象能正确反映出S与t的函数关系的是（　　）

A．
B．
C．
D．
八．一次函数的图象（共1小题）
10．（2022•辽宁）如图，在同一平面直角坐标系中，一次函数y＝k1x+b1与y＝k2x+b2的图象分别为直线l1和直线l2，下列结论正确的是（　　）

A．k1•k2＜0 B．k1+k2＜0 C．b1﹣b2＜0 D．b1•b2＜0
九．二次函数图象与系数的关系（共1小题）
11．（2022•辽宁）抛物线y＝ax2+bx+c的部分图象如图所示，对称轴为直线x＝﹣1，直线y＝kx+c与抛物线都经过点（﹣3，0）．下列说法：①ab＞0；②4a+c＞0；③若（﹣2，y1）与（，y2）是抛物线上的两个点，则y1＜y2；④方程ax2+bx+c＝0的两根为x1＝﹣3，x2＝1；⑤当x＝﹣1时，函数y＝ax2+（b﹣k）x有最大值．其中正确的个数是（　　）

A．2 B．3 C．4 D．5
一十．二次函数综合题（共1小题）
12．（2022•丹东）如图，抛物线y＝ax2+bx+c（a≠0）与x轴交于点A（5，0），与y轴交于点C，其对称轴为直线x＝2，结合图象分析如下结论：①abc＞0；②b+3a＜0；③当x＞0时，y随x的增大而增大；④若一次函数y＝kx+b（k≠0）的图象经过点A，则点E（k，b）在第四象限；⑤点M是抛物线的顶点，若CM⊥AM，则a＝．其中正确的有（　　）

A．1个 B．2个 C．3个 D．4个
一十一．平行线的性质（共2小题）
13．（2022•营口）如图，直线DE∥FG，Rt△ABC的顶点B，C分别在DE，FG上，若∠BCF＝25°，则∠ABE的大小为（　　）

A．55° B．25° C．65° D．75°
14．（2022•辽宁）如图，直线m∥n，AC⊥BC于点C，∠1＝30°，则∠2的度数为（　　）

A．140° B．130° C．120° D．110°
一十二．圆内接四边形的性质（共1小题）
15．（2022•营口）如图，点A，B，C，D在⊙O上，AC⊥BC，AC＝4，∠ADC＝30°，则BC的长为（　　）

A．4 B．8 C．4 D．4
一十三．弧长的计算（共1小题）
16．（2022•丹东）如图，AB是⊙O的直径，C是⊙O上一点，连接AC，OC，若AB＝6，∠A＝30°，则的长为（　　）

A．6π B．2π C．π D．π
一十四．扇形面积的计算（共1小题）
17．（2022•鞍山）如图，在矩形ABCD中，AB＝2，BC＝，以点B为圆心，BA长为半径画弧，交CD于点E，连接BE，则扇形BAE的面积为（　　）

A． B． C． D．
一十五．作图—基本作图（共2小题）
18．（2022•辽宁）如图，OG平分∠MON，点A，B是射线OM，ON上的点，连接AB．按以下步骤作图：①以点B为圆心，任意长为半径作弧，交AB于点C，交BN于点D；②分别以点C和点D为圆心，大于CD长为半径作弧，两弧相交于点E；③作射线BE，交OG于点P．若∠ABN＝140°，∠MON＝50°，则∠OPB的度数为（　　）

A．35° B．45° C．55° D．65°
19．（2022•营口）如图，在△ABC中，AB＝AC，∠A＝36°，由图中的尺规作图得到的射线与AC交于点D，则以下推断错误的是（　　）

A．BD＝BC B．AD＝BD C．∠ADB＝108° D．CD＝AD
一十六．作图—复杂作图（共1小题）
20．（2022•盘锦）如图，线段AB是半圆O的直径．分别以点A和点O为圆心，大于的长为半径作弧，两弧交于M，N两点，作直线MN，交半圆O于点C，交AB于点E，连接AC，BC，若AE＝1，则BC的长是（　　）

A． B．4 C．6 D．


参考答案与试题解析
一．实数大小比较（共1小题）
1．（2022•营口）在，0，﹣1，2这四个实数中，最大的数是（　　）
A．0 B．﹣1 C．2 D．
【解答】解：∵﹣1＜0＜＜2，
∴最大的数是2；
故选：C．
二．同底数幂的除法（共1小题）
2．（2022•辽宁）下列运算正确的是（　　）
A．（a2）4＝a6 B．a2•a4＝a6 C．a2+a4＝a6 D．a2÷a4＝a6
【解答】解：A．（a2）4＝a8，故A选项错误；
B．a2•a4＝a6，故B选项正确；
C．a2+a4≠a6，故C选项错误；
D．a2÷a4＝a﹣2＝，故D选项错误；
故选：B．
三．单项式乘单项式（共1小题）
3．（2022•辽宁）下列运算正确的是（　　）
A．2a2•3a＝6a3 B．（2a）3＝2a3
C．a6÷a2＝a3 D．3a2+2a3＝5a5
【解答】解：A、2a2•3a＝6a3，故A符合题意；
B、（2a）3＝8a3，故B不符合题意；
C、a6÷a2＝a4，故C不符合题意；
D、3a2与2a3不能合并，故D不符合题意；
故选：A．
四．由实际问题抽象出二元一次方程组（共1小题）
4．（2022•盘锦）《九章算术》是中国传统数学重要的著作，奠定了中国传统数学的基本框架．其中《盈不足》卷记载了一道有趣的数学问题：“今有共买物，人出八，赢三；人出七，不足四．问人数、物价各几何？”译文：“今有人合伙购物，每人出8钱，会多出3钱；每人出7钱，又差4钱．问人数、物价各多少？”设人数为x人，物价为y钱，根据题意，下面所列方程组正确的是（　　）

A． B．
C． D．
【解答】解：设人数为x人，物价为y钱，
依题意得：．
故选：B．
五．根的判别式（共2小题）
5．（2022•辽宁）下列一元二次方程无实数根的是（　　）
A．x2+x﹣2＝0 B．x2﹣2x＝0 C．x2+x+5＝0 D．x2﹣2x+1＝0
【解答】解：A、Δ＝12﹣4×1×（﹣2）＝9＞0，则该方程有两个不相等的实数根，故本选项不符合题意；
B、Δ＝（﹣2）2﹣4×1×0＝4＞0，则该方程有两个不相等的实数根，故本选项不符合题意；
C、Δ＝12﹣4×1×5＝﹣19＜0，则该方程无实数根，故本选项符合题意；
D、Δ＝（﹣2）2﹣4×1×1＝0，则该方程有两个相等的实数根，故本选项不符合题意；
故选：C．
6．（2022•营口）关于x的一元二次方程x2+4x﹣m＝0有两个实数根，则实数m的取值范围为（　　）
A．m＜4 B．m＞﹣4 C．m≤4 D．m≥﹣4
【解答】解：∵关于x的一元二次方程x2+4x﹣m＝0有两个实数根，
∴Δ＝42﹣4×1×（﹣m）＝16+4m≥0，
解得：m≥﹣4，
故选：D．
六．解分式方程（共1小题）
7．（2022•营口）分式方程＝的解是（　　）
A．x＝2 B．x＝﹣6 C．x＝6 D．x＝﹣2
【解答】解：＝，
方程两边都乘x（x﹣2），得3（x﹣2）＝2x，
解得：x＝6，
检验：当x＝6时，x（x﹣2）≠0，
所以x＝6是原方程的解，
即原方程的解是x＝6，
故选：C．
七．动点问题的函数图象（共2小题）
8．（2022•辽宁）如图，在等边三角形ABC中，BC＝4，在Rt△DEF中，∠EDF＝90°，∠F＝30°，DE＝4，点B，C，D，E在一条直线上，点C，D重合，△ABC沿射线DE方向运动，当点B与点E重合时停止运动．设△ABC运动的路程为x，△ABC与Rt△DEF重叠部分的面积为S，则能反映S与x之间函数关系的图象是（　　）

A．
B．
C．
D．
【解答】解：过点A作AM⊥BC，交BC于点M，

在等边△ABC中，∠ACB＝60°，
在Rt△DEF中，∠F＝30°，
∴∠FED＝60°，
∴∠ACB＝∠FED，
∴AC∥EF，
在等边△ABC中，AM⊥BC，
∴BM＝CM＝BC＝2，AM＝BM＝2，
∴S△ABC＝BC•AM＝4，
①当0＜x≤2时，设AC与DF交于点G，此时△ABC与Rt△DEF重叠部分为△CDG，

由题意可得CD＝x，DG＝x
∴S＝CD•DG＝x2；
②当2＜x≤4时，设AB与DF交于点G，此时△ABC与Rt△DEF重叠部分为四边形AGDC，

由题意可得：CD＝x，则BC＝4﹣x，DG＝（4﹣x），
∴S＝S△ABC﹣S△BDG＝4﹣×（4﹣x）×（4﹣x），
∴S＝﹣x2+4x﹣4＝﹣（x﹣4）2+4，
③当4＜x≤8时，设AB与EF交于点G，过点G作GM⊥BC，交BC于点M，
此时△ABC与Rt△DEF重叠部分为△BEG，

由题意可得CD＝x，则CE＝x﹣4，DB＝x﹣4，
∴BE＝x﹣（x﹣4）﹣（x﹣4）＝8﹣x，
∴BM＝4﹣x
在Rt△BGM中，GM＝（4﹣x），
∴S＝BE•GM＝（8﹣x）×（4﹣x），
∴S＝（x﹣8）2，
综上，选项A的图像符合题意，
故选：A．
9．（2022•盘锦）如图，四边形ABCD是边长为2cm的正方形，点E，点F分别为边AD，CD中点，点O为正方形的中心，连接OE，OF，点P从点E出发沿E﹣O﹣F运动，同时点Q从点B出发沿BC运动，两点运动速度均为1cm/s，当点P运动到点F时，两点同时停止运动，设运动时间为ts，连接BP，PQ，△BPQ的面积为Scm2，下列图象能正确反映出S与t的函数关系的是（　　）

A．
B．
C．
D．
【解答】解：当0≤t≤1时，
∵正方形ABCD的边长为2，点O为正方形的中心，
∴直线EO垂直BC，
∴点P到直线BC的距离为2﹣t，BQ＝t，
∴S＝；
当1＜t≤2时，
∵正方形ABCD的边长为2，点E，点F分别为边AD，CD中点，点O为正方形的中心，
∴直线OF∥BC，
∴点P到直线BC的距离为1，BQ＝t，
∴S＝；
故选D．
八．一次函数的图象（共1小题）
10．（2022•辽宁）如图，在同一平面直角坐标系中，一次函数y＝k1x+b1与y＝k2x+b2的图象分别为直线l1和直线l2，下列结论正确的是（　　）

A．k1•k2＜0 B．k1+k2＜0 C．b1﹣b2＜0 D．b1•b2＜0
【解答】解：∵一次函数y＝k1x+b1的图象过一、二、三象限，
∴k1＞0，b1＞0，
∵一次函数y＝k2x+b2的图象过一、三、四象限，
∴k2＞0，b2＜0，
∴A、k1•k2＞0，故A不符合题意；
B、k1+k2＞0，故B不符合题意；
C、b1﹣b2＞0，故C不符合题意；
D、b1•b2＜0，故D符合题意；
故选：D．
九．二次函数图象与系数的关系（共1小题）
11．（2022•辽宁）抛物线y＝ax2+bx+c的部分图象如图所示，对称轴为直线x＝﹣1，直线y＝kx+c与抛物线都经过点（﹣3，0）．下列说法：①ab＞0；②4a+c＞0；③若（﹣2，y1）与（，y2）是抛物线上的两个点，则y1＜y2；④方程ax2+bx+c＝0的两根为x1＝﹣3，x2＝1；⑤当x＝﹣1时，函数y＝ax2+（b﹣k）x有最大值．其中正确的个数是（　　）

A．2 B．3 C．4 D．5
【解答】解：∵抛物线的开口方向向下，
∴a＜0．
∵抛物线的对称轴为直线x＝﹣1，
∴﹣＝﹣1，
∴b＝2a，b＜0．
∵a＜0，b＜0，
∴ab＞0，
∴①的结论正确；
∵抛物线y＝ax2+bx+c经过点（﹣3，0），
∴9a﹣3b+c＝0，
∴9a﹣3×2a+c＝0，
∴3a+c＝0．
∴4a+c＝a＜0，
∴②的结论不正确；
∵抛物线的对称轴为直线x＝﹣1，
∴点（﹣2，y1）关于直线x＝﹣1对称的对称点为（0，y1），
∵a＜0，
∴当x＞﹣1时，y随x的增大而减小．
∵＞0＞﹣1，
∴y1＞y2．
∴③的结论不正确；
∵抛物线的对称轴为直线x＝﹣1，抛物线经过点（﹣3，0），
∴抛物线一定经过点（1，0），
∴抛物线y＝ax2+bx+c与x轴的交点的横坐标为﹣3，1，
∴方程ax2+bx+c＝0的两根为x1＝﹣3，x2＝1，
∴④的结论正确；
∵直线y＝kx+c经过点（﹣3，0），
∴﹣3k+c＝0，
∴c＝3k．
∵3a+c＝0，
∴c＝﹣3a，
∴3k＝﹣3a，
∴k＝﹣a．
∴函数y＝ax2+（b﹣k）x
＝ax2+（2a+a）x
＝ax2+3ax
＝a﹣a，
∵a＜0，
∴当x＝﹣时，函数y＝ax2+（b﹣k）x有最大值，
∴⑤的结论不正确．
综上，结论正确的有：①④，
故选：A．
一十．二次函数综合题（共1小题）
12．（2022•丹东）如图，抛物线y＝ax2+bx+c（a≠0）与x轴交于点A（5，0），与y轴交于点C，其对称轴为直线x＝2，结合图象分析如下结论：①abc＞0；②b+3a＜0；③当x＞0时，y随x的增大而增大；④若一次函数y＝kx+b（k≠0）的图象经过点A，则点E（k，b）在第四象限；⑤点M是抛物线的顶点，若CM⊥AM，则a＝．其中正确的有（　　）

A．1个 B．2个 C．3个 D．4个
【解答】解：∵抛物线开口向上，
∴a＞0，
∵对称轴是直线x＝2，
∴﹣＝2，
∴b＝﹣4a＜0
∵抛物线交y轴的负半轴，
∴c＜0，
∴abc＞0，故①正确，
∵b＝﹣4a，a＞0，
∴b+3a＝﹣a＜0，故②正确，
观察图象可知，当0＜x≤2时，y随x的增大而减小，故③错误，
一次函数y＝kx+b（k≠0）的图象经过点A，
∵b＜0，
∴k＞0，此时E（k，b）在第四象限，故④正确．
∵抛物线经过（﹣1，0），（5，0），
∴可以假设抛物线的解析式为y＝a（x+1）（x﹣5）＝a（x﹣2）2﹣9a，
∴M（2，﹣9a），C（0，﹣5a），
过点M作MH⊥y轴于点H，设对称轴交x轴于点K．
∵AM⊥CM，
∴∠AMC＝∠KMH＝90°，
∴∠CMH＝∠KMA，
∵∠MHC＝∠MKA＝90°，
∴△MHC∽△MKA，
∴＝，
∴＝，
∴a2＝，
∵a＞0，
∴a＝，故⑤正确，
故选：D．

一十一．平行线的性质（共2小题）
13．（2022•营口）如图，直线DE∥FG，Rt△ABC的顶点B，C分别在DE，FG上，若∠BCF＝25°，则∠ABE的大小为（　　）

A．55° B．25° C．65° D．75°
【解答】解：∵DE∥FG，∠BCF＝25°，
∴∠CBE＝∠BCF＝25°，
∵∠ABC＝90°，
∴∠ABE＝∠ABC﹣∠CBE＝65°．
故选：C．
14．（2022•辽宁）如图，直线m∥n，AC⊥BC于点C，∠1＝30°，则∠2的度数为（　　）

A．140° B．130° C．120° D．110°
【解答】解：∵AC⊥BC于点C，
∴∠ACB＝90°，
∴∠ABC+∠1＝90°，
∴∠ABC＝90°﹣30°＝60°，
∵m∥n，
∴∠2＝180°﹣∠ABC＝120°．
故选：C．
一十二．圆内接四边形的性质（共1小题）
15．（2022•营口）如图，点A，B，C，D在⊙O上，AC⊥BC，AC＝4，∠ADC＝30°，则BC的长为（　　）

A．4 B．8 C．4 D．4
【解答】解：连接AB，如图所示，

∵AC⊥BC，
∴∠ACB＝90°．
∵∠ADC＝30°，
∴∠ABC＝∠ADC＝30°．
∴在Rt△ABC中，
tan∠ABC＝，
∴BC＝．
∵AC＝4，
∴BC＝＝4．
故选：A．
一十三．弧长的计算（共1小题）
16．（2022•丹东）如图，AB是⊙O的直径，C是⊙O上一点，连接AC，OC，若AB＝6，∠A＝30°，则的长为（　　）

A．6π B．2π C．π D．π
【解答】解：∵直径AB＝6，
∴半径OB＝3，
∵圆周角∠A＝30°，
∴圆心角∠BOC＝2∠A＝60°，
∴的长是＝π，
故选：D．
一十四．扇形面积的计算（共1小题）
17．（2022•鞍山）如图，在矩形ABCD中，AB＝2，BC＝，以点B为圆心，BA长为半径画弧，交CD于点E，连接BE，则扇形BAE的面积为（　　）

A． B． C． D．
【解答】解：∵四边形ABCD是矩形，
∴∠ABC＝∠C＝90°，
∵BA＝BE＝2，BC＝，
∴cos∠CBE＝＝，
∴∠CBE＝30°，
∴∠ABE＝90°﹣30°＝60°，
∴S扇形BAE＝＝，
故选：C．
一十五．作图—基本作图（共2小题）
18．（2022•辽宁）如图，OG平分∠MON，点A，B是射线OM，ON上的点，连接AB．按以下步骤作图：①以点B为圆心，任意长为半径作弧，交AB于点C，交BN于点D；②分别以点C和点D为圆心，大于CD长为半径作弧，两弧相交于点E；③作射线BE，交OG于点P．若∠ABN＝140°，∠MON＝50°，则∠OPB的度数为（　　）

A．35° B．45° C．55° D．65°
【解答】解：由作法得BP平分∠ABN，
∴∠PBN＝∠ABN＝×140°＝70°，
∵OG平分∠MON，
∴∠BOP＝∠MON＝×50°＝25°，
∵∠PBN＝∠POB+∠OPB，
∴∠OPB＝70°﹣25°＝45°．
故选：B．
19．（2022•营口）如图，在△ABC中，AB＝AC，∠A＝36°，由图中的尺规作图得到的射线与AC交于点D，则以下推断错误的是（　　）

A．BD＝BC B．AD＝BD C．∠ADB＝108° D．CD＝AD
【解答】解：在△ABC中，
∵AB＝AC，
∴∠ABC＝∠ACB．
∵∠A＝36°，
∴∠ABC＝∠C＝（180°﹣36°）＝72°．
∵BD平分∠ABC，
∴∠ABD＝∠CBD＝36°．
∴∠ABD＝∠A．
∴AD＝BD．故选项B正确；
∵∠BDC＝∠A+∠ABD＝72°．
∴∠C＝∠BDC．
∴BD＝BC．故选项A正确；
∵∠BDC＝72°，
∴∠ADB＝108°．故选项C正确；
在△BCD与△ACB中，
∵∠CBD＝∠A＝36°，∠C为公共角．
∴△BCD∽△ACB．
∴．
∴BC2＝AC•CD．
∵BC＝BD＝AD，AC＝AD+CD．
∴AD2＝（AD+CD）•CD．整理得，CD2﹣AD•CD﹣AD2＝0．
解得，CD＝AD．
∴CD≠AD．故选项D错误．
故选：D．
一十六．作图—复杂作图（共1小题）
20．（2022•盘锦）如图，线段AB是半圆O的直径．分别以点A和点O为圆心，大于的长为半径作弧，两弧交于M，N两点，作直线MN，交半圆O于点C，交AB于点E，连接AC，BC，若AE＝1，则BC的长是（　　）

A． B．4 C．6 D．
【解答】解：如图，连接OC．
根据作图知CE垂直平分AO，
∴AC＝OC，AE＝OE＝1，
∴OC＝OB＝AO＝AE+EO＝2，
∴AC＝OC＝AO＝AE+EO＝2，
即AB＝AO+BO＝4，
∵线段AB是半圆O的直径，
∴∠ACB＝90°，
在Rt△ACB中，根据勾股定理得，，
故选A．