初中数学2.2 一元二次方程的解法同步达标检测题

这是一份初中数学2.2 一元二次方程的解法同步达标检测题，共3页。


解一元二次方程需根据方程特点选用适当方法，一般情况下：（1）首先看能否用平方根的意义或因式分解法；（2）不能用以上方法的可考虑公式法；（3）除特别指明外，一般不用配方法.[来源:*&^中教%网#]
基础导练
一元二次方程x2-4x+2=0的根是 ___________.[来^源#:中教&~网%]
2.已知x=1是一元二次方程x2+m x+n=0的一个根，则m+n的值是______.
3.一元二次方程x2+5x+6=0的根是__________.[来源*:中国教育出版^@网&~]
4.方程x2-x-12=0的解是___________.
5.下列方程中，不能用平方根的意义求解的是( )
A.x2-3=0 B.(x-1)2-4=0 C.x2+2x=0 D.(x-1)2=(2x+1)2[来源:zzste&p%#.c^m@]
6.用配方法解一元二次方程x2-2x-3=0时，方程变形正确的是( )
A.(x-1)2=2 B.(x-1)2=4 C.(x-2)2=1 D.(x-2)2=7[来&源:@中教#~*网]
7.方程4(x-3)2+x(x-3)=0的根为( )
A.x=3 B.x= C.x1=-3，x2= D.x1=3，x2=
8.方程x2+x-1=0的根是( )
A.1- B. C.-1+ D.
9.阅读材料：对于任何实数，我们规定符号的意义是=ad-bc.
例如：=1×4-2×3=-2，=(-2)×5-4×3=-22.
(1)按照这个规定请你计算的值；
(2)按照这个规定请你计算：当x2-4x+4=0时，的值.
10.已知△ABC的两边长分别为2和3，第三边长是方程(x2-2x)-5(x-2)=0的根，求△ABC的周长.
11.分解因式x2+2x-1.
参考答案
x1=2+，x2=2- 2.-1 3.x1=-2，x2=-3 4.x1=4，x2=-3 5.C 6.B 7.D 8.D
9. (1)=5×8-6×7=-2.
（2）由x2-4x+4=0得x=2，==3×1-4×1=-1.
10.原方程可化为x(x-2)-5(x-2)=0，∴(x-5)(x-2)=0，∴x1=5，x2=2.
∵三角形任意两边之和大于第三边，任意两边之差小于第三边，
∴第三边的长x的取值范围是1∴△ABC的周长为2+3+2=7.
[ww#w.zzs^tep.~*cm%]
11..解：x2+2x-1
= x2+2x+1-1-1
= (x+1)2-2
= (x+1+) (x+1-)
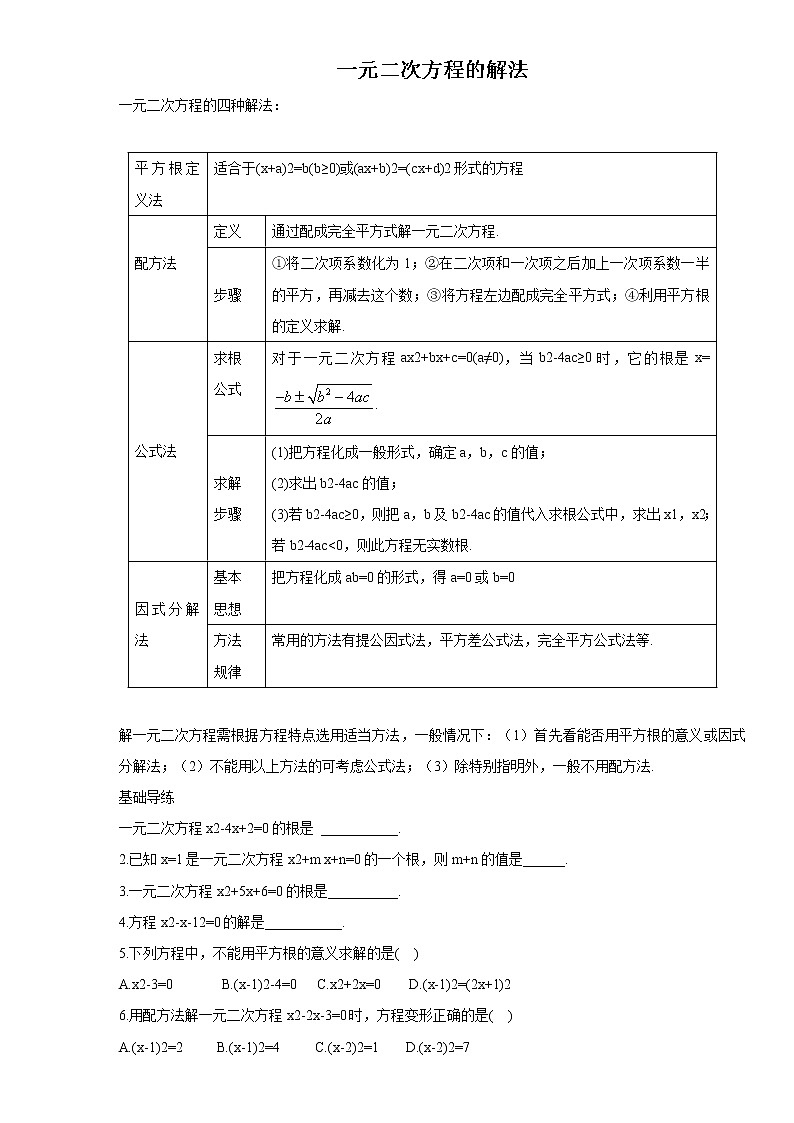
[来源:%^中教网~#&]平方根定义法
适合于(x+a)2=b(b≥0)或(ax+b)2=(cx+d)2形式的方程
配方法
定义
通过配成完全平方式解一元二次方程.
步骤
①将二次项系数化为1；②在二次项和一次项之后加上一次项系数一半的平方，再减去这个数；③将方程左边配成完全平方式；④利用平方根的定义求解.
公式法
求根
公式
对于一元二次方程ax2+bx+c=0(a≠0)，当b2-4ac≥0时，它的根是x=.
求解
步骤
(1)把方程化成一般形式，确定a，b，c的值；
(2)求出b2-4ac的值；
(3)若b2-4ac≥0，则把a，b及b2-4ac的值代入求根公式中，求出x1，x2；若b2-4ac<0，则此方程无实数根.
因式分解法
基本
思想
把方程化成ab=0的形式，得a=0或b=0
方法
规律
常用的方法有提公因式法，平方差公式法，完全平方公式法等.