



第2节 抛体运动-2023年高考物理二轮复习对点讲解与练习(通用版)
展开第四章 曲线运动 万有引力与航天
第2节 抛体运动
考点一 平抛运动的规律及应用
【知识梳理】
1.定义(条件):以一定的初速度沿水平方向抛出的物体只在重力作用下的运动。
2.运动性质:平抛运动是加速度为g的匀变速曲线运动,其运动轨迹是抛物线。
3.研究方法:平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动。
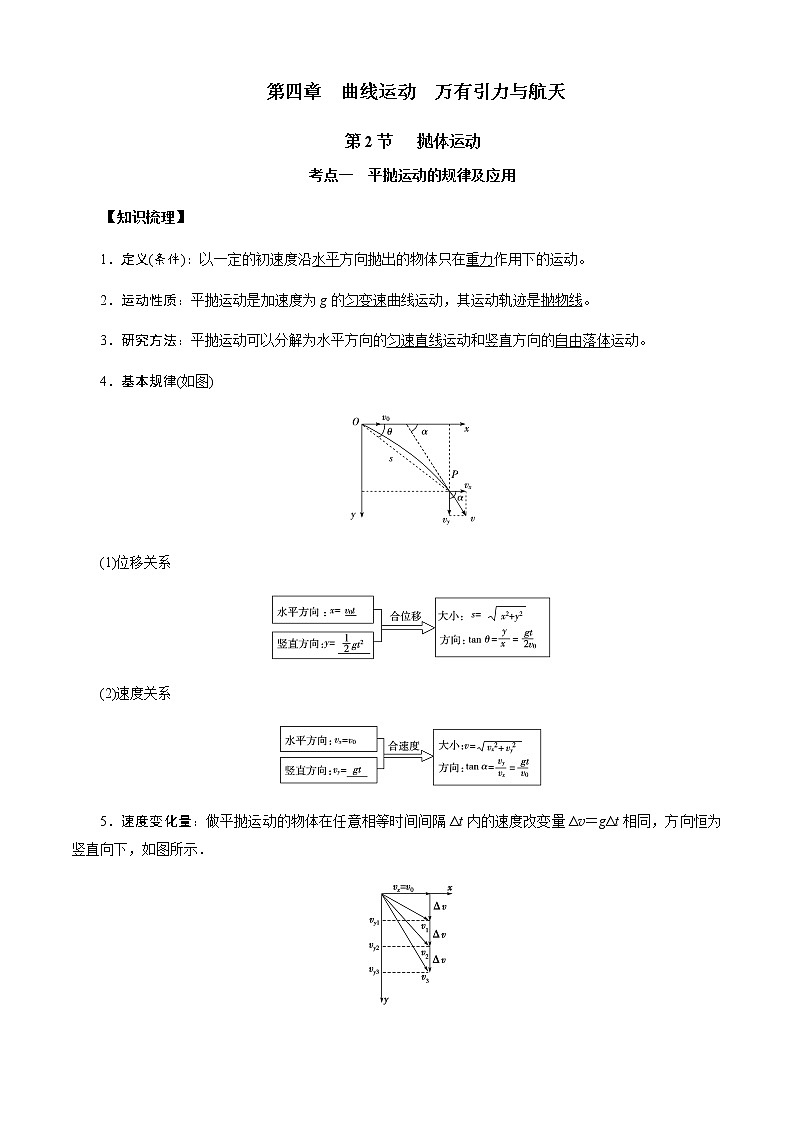
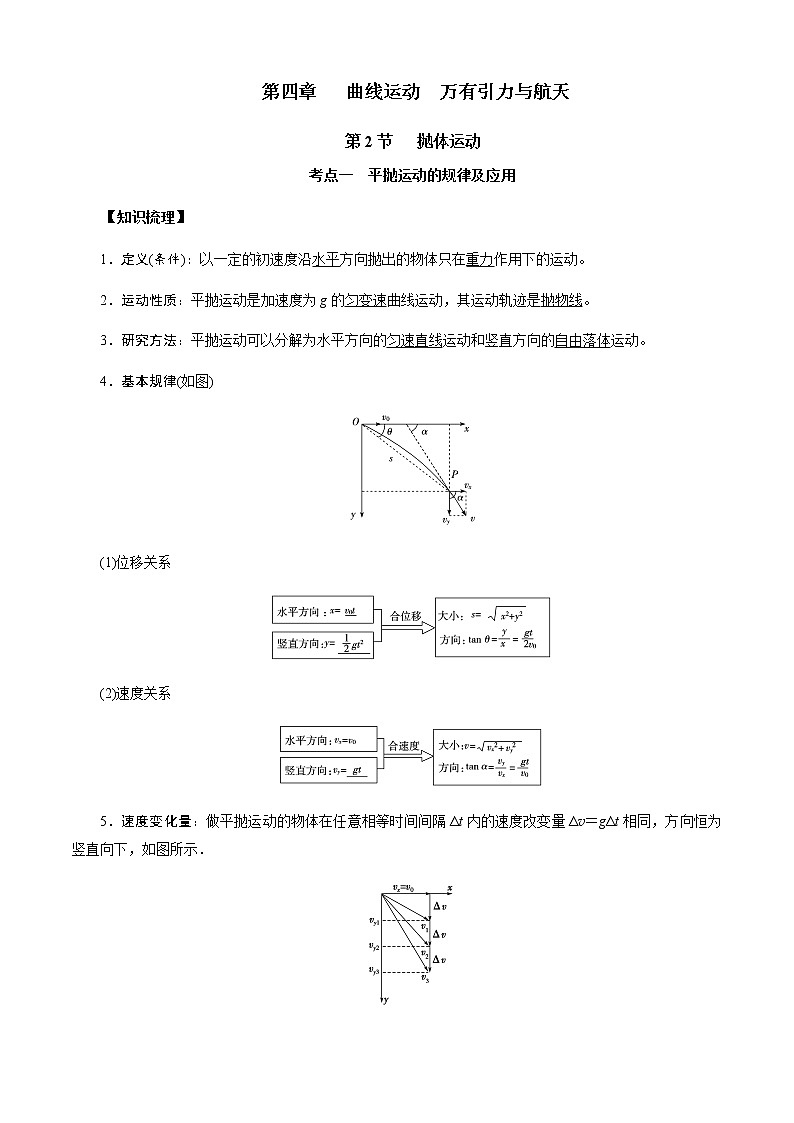
4.基本规律(如图)
(1)位移关系
(2)速度关系
5.速度变化量:做平抛运动的物体在任意相等时间间隔Δt内的速度改变量Δv=gΔt相同,方向恒为竖直向下,如图所示.
6.两个重要推论:
(1)做平抛(或类平抛)运动的物体任一时刻的瞬时速度的反向延长线一定通过此时水平位移的中点,如图所示.
(2)做平抛(或类平抛)运动的物体在任一时刻任一位置处,设其速度方向与水平方向的夹角为θ,位移与水平方向的夹角为α,则tan θ=2tan α.
【诊断小练】
(1)做平抛运动的物体的速度方向时刻在变化,加速度方向也时刻在变化.( )
(2)无论初速度是斜向上方还是斜向下方的斜抛运动都是匀变速曲线运动.( )
(3)做平抛运动的物体质量越大,水平位移越大.( )
(4)做平抛运动的物体初速度越大,落地时竖直方向的速度越大.( )
(5)从同一高度水平抛出的物体,不计空气阻力,初速度大的落地速度大.( )
(6)无论平抛运动还是斜抛运动,都是匀变速曲线运动.( )
(7)做平抛运动的物体,在任意相等的时间内速度的变化量是相同的.( )
【答案】 (1)× (2)√ (3)× (4)× (5)√ (6)√ (7)√
【命题突破】
命题点1 平抛运动的规律及应用
1.关于平抛运动的叙述,下列说法不正确的是( )
A.平抛运动是一种在恒力作用下的曲线运动
B.平抛运动的速度方向与恒力方向的夹角保持不变
C.平抛运动的速度大小是时刻变化的
D.平抛运动的速度方向与加速度方向的夹角一定越来越小
【解析】选B 做平抛运动的物体只受重力作用,故平抛运动是匀变速曲线运动,A说法正确;平抛运动是曲线运动,速度的方向时刻变化,即与恒力方向的夹角时刻改变,B说法错误;平抛运动是匀变速运动,速度大小时刻变化,C说法正确;设水平初速度为v0,速度方向与加速度方向(竖直方向)的夹角为θ,有tan θ=,可知随着时间增加,夹角θ变小,D说法正确。本题选择说法不正确的,故B符合题意。
【解析】 B
2.发球机从同一高度向正前方依次水平射出两个速度不同的乒乓球(忽略空气的影响).速度较大的球越过球网,速度较小的球没有越过球网.其原因是( )
A.速度较小的球下降相同距离所用的时间较多
B.速度较小的球在下降相同距离时在竖直方向上的速度较大
C.速度较大的球通过同一水平距离所用的时间较少
D.速度较大的球在相同时间间隔内下降的距离较大
【解析】 在竖直方向,球做自由落体运动,由h= gt2知,选项A、D错误.
由v2=2gh知,选项B错误.
在水平方向,球做匀速直线运动,通过相同水平距离,速度大的球用时少,选项C正确.
【答案】 C
3.如图所示,从倾角为θ的斜面上的A点以初速度v0水平抛出一个物体,物体落在斜面上的B点,不计空气阻力.求:
(1)抛出后经多长时间物体与斜面间距离最大?
(2)A、B间的距离为多少?
【解析】
解法一:以抛出点为坐标原点沿斜面方向为x轴,垂直于斜面方向为y轴,建立坐标系,(如图所示)
vx=v0cos θ,vy=v0sin θ,
ax=gsin θ,ay=gcos θ.
物体沿斜面方向做初速度为vx,加速度为ax的匀加速直线运动,垂直于斜面方向做初速度为vy,加速度为ay的匀减速直线运动,类似于竖直上抛运动.
(1)令vy′=v0sin θ-gcos θ·t=0,即t=,
(2)当t=时,离斜面最远,由对称性可知总飞行时间T=2t=,
AB间距离x=s=v0cos θ·T+gsin θ·T2=.
解法二:(1)如图所示当速度方向与斜面平行时,离斜面最远,v的切线反向延长与v0交点为横坐标的中点P,则tan θ==,t=.
(2)=y=gt2=,
而∶=1∶3,
所以=Y=4y=,
AB间距离s==.
解法三:(1)设物体运动到C点离斜面最远,所用时间为t,将v分解成vx和vy,如图甲所示,则由tan θ==,得t=.
(2)设由A到B所用时间为t′,水平位移为x,竖直位移为y,如图乙所示,
由图可得tan θ=,y=xtan θ①
y=gt′2②
x=v0t′③
由①②③得:t′=
而x=v0t′=,
因此A、B间的距离s==.
【答案】 (1) (2)
命题点2 类平抛运动
4.(多选)一位同学玩投掷飞镖游戏时,将飞镖水平抛出后击中目标。当飞镖在飞行过程中速度的方向平行于抛出点与目标间的连线时,其大小为v。不考虑空气阻力,已知连线与水平面间的夹角为θ,则飞镖( )
A.初速度v0=vcos θ
B.飞行时间t=
C.飞行的水平距离x=
D.飞行的竖直距离y=
【解析】选AC 根据运动的合成与分解知飞镖的初速度v0=vcos θ,选项A正确;根据平抛运动的规律有x=v0t,y=gt2,tan θ=,解得t=,x=,y=,选项C正确,B、D错误。
【答案】 AC
5.如图所示,两个倾角分别为30°、45°的光滑斜面放在同一水平面上,斜面高度相等.有三个完全相同的小球a、b、c,开始均静止于同一高度处,其中b小球在两斜面之间,a、c两小球在斜面顶端,两斜面间距大于小球直径.若同时释放,a、b、c小球到达水平面的时间分别为t1、t2、t3.若同时沿水平方向抛出,初速度方向如图所示,到达水平面的时间分别为t1′、t2′、t3′.下列关于时间的关系正确的是( )
A.t1>t3>t2 B.t1=t1′、t2=t2′、t3=t3′
C.t1′>t3′>t2′ D.t1<t1′、t2<t2′、t3<t3′
【解析】 由静止释放三小球时,
对a:=gsin 30°·t,则t=.
对b:h=gt,则t=.
对c:=gsin 45°·t,则t=.
所以t1>t3>t2.
当平抛三小球时:小球b做平抛运动,竖直方向运动情况同第一次情况,小球a、c在斜面内做类平抛运动,沿斜面向下方向的运动同第一次情况,所以t1=t1′、t2=t2′、t3=t3′.故选A、B、C.
【答案】 ABC
【归纳总结】
分解思想在平抛运动中的应用
(1)解答平抛运动问题时,一般的方法是将平抛运动沿水平和竖直两个方向分解,这样分解的优点是不用分解初速度也不用分解加速度.
(2)画出速度(或位移)分解图,通过几何知识建立合速度(或合位移)、分速度(或分位移)及其方向间的关系,通过速度(或位移)的矢量三角形求解未知量.
考点二 多体平抛运动问题分析
【知识梳理】
1.多体平抛运动问题是指多个物体在 同一竖直平面内 平抛时所涉及的问题.
2.三类常见的多体平抛运动
(1)若两物体同时从同一高度(或同一点)抛出,则两物体始终在 同一 高度,二者间距只取决于两物体的 水平 分运动.
(2)若两物体同时从不同高度抛出,则两物体高度差始终与抛出点高度差 相同 ,二者间距由两物体的 水平分运动 和 竖直高度差 决定.
(3)若两物体从同一点先后抛出,两物体竖直高度差随时间 均匀增大 ,二者间距取决于两物体的水平分运动和竖直分运动.
3. 对多体平抛问题的四点提醒
(1)两条平抛运动轨迹的交点是两物体的必经之处,两物体要在此处相遇,必须同时到达此处。即轨迹相交是物体相遇的必要条件。
(2)若两物体同时从同一高度抛出,则两物体始终处在同一高度。
(3)若两物体同时从不同高度抛出,则两物体高度差始终与抛出点高度差相同。
(4)若两物体从同一高度先后抛出,则两物体高度差随时间均匀增大。
【命题突破】
命题点1 从同一竖直线(同一点)抛出多个物体问题
1.如图所示,x轴在水平地面上,y轴在竖直方向上.图中画出了从y轴上不同位置沿x轴正向水平抛出的三个小球a、b和c的运动轨迹.小球a从(0,2L)抛出,落在(2L,0)处;小球b、c从(0,L)抛出,分别落在(2L,0)和(L,0)处.不计空气阻力,下列说法正确的是( )
A.a和b初速度相同
B.b和c运动时间相同
C.b的初速度是c的两倍
D.a运动时间是b的两倍
【解析】 b、c的高度相同,小于a的高度,根据h=gt2,得t=,知b、c的运动时间相同,a的运动时间是b的运动时间的倍.故B正确,D错误;因为a的运动时间长,但是水平位移相同,根据x=v0t知,a的水平速度小于b的水平速度.故A错误;b、c的运动时间相同,b的水平位移是c的水平位移的两倍,则b的初速度是c的初速度的两倍.故C正确.故选B、C.
【答案】 BC
命题点2 从不同竖直线上抛出多个物体问题
2.如图所示,A、B两小球从相同高度同时水平抛出,经过时间t在空中相遇。若两球的抛出速度都变为原来的2倍,则两球从抛出到相遇经过的时间为( )
A.t B.t
C. D.
【解析】选C 设两球间的水平距离为L,第一次抛出的速度分别为v1、v2,由于小球抛出后在水平方向上做匀速直线运动,则从抛出到相遇经过的时间t=,若两球的抛出速度都变为原来的2倍,则从抛出到相遇经过的时间为t′==,C项正确。
【答案】 C
【归纳总结】
(1)物体做平抛运动的时间由物体被抛出点的高度决定,而物体的水平位移由物体被抛出点的高度和物体的初速度共同决定.
(2)两条平抛运动轨迹的相交处是两物体的可能相遇处,两物体要在此处相遇,必须同时到达此处.
考点三 落点有约束条件的平抛运动
考法(一) 落点在斜面上的平抛运动
1.(多选)如图所示,一固定斜面倾角为θ,将小球A从斜面顶端以速率v0水平向右抛出,小球击中了斜面上的P点;将小球B从空中某点以相同速率v0水平向左抛出,小球恰好垂直斜面击中Q点。不计空气阻力,重力加速度为g,下列说法正确的是( )
A.若小球A在击中P点时速度方向与水平方向所夹锐角为φ,则tan θ=2tan φ
B.若小球A在击中P点时速度方向与水平方向所夹锐角为φ,则tan φ=2tan θ
C.小球A、B在空中运动的时间之比为2tan2θ∶1
D.小球A、B在空中运动的时间之比为tan2θ∶1
【解析】 由题图可知,斜面的倾角θ等于小球A落在斜面上时的位移与水平方向的夹角,由平抛运动的推论可知,tan φ=2tan θ,选项B正确,A错误;设小球A在空中运动的时间为t1,小球B在空中运动的时间为t2,则由平抛运动的规律可得tan θ=,tan θ=,故=2tan2θ,选项C正确,D错误。
【答案】 BC
【题型技法】
图示
方法
基本规律
运动时间
分解速度,构建速度的矢量三角形
水平vx=v0
竖直vy=gt
合速度v=
由tan θ==得t=
分解位移,构建位移的矢量三角形
水平x=v0t
竖直y=gt2
合位移x合=
由tan θ==
得t=
在运动起点同时分解v0、g
由0=v1-a1t,0-v12=-2a1d得t=,d=
分解平行于斜面的速度v
由vy=gt得t=
考法(二) 落点在竖直面上的平抛运动
2.(多选)从竖直墙的前方A处,沿AO方向水平发射三颗弹丸a、b、c,在墙上留下的弹痕如图所示。已知Oa=ab=bc,则a、b、c三颗弹丸(不计空气阻力)( )
A.初速度之比是∶∶
B.初速度之比是1∶∶
C.从射出至打到墙上过程速度增量之比是1∶∶
D.从射出至打到墙上过程速度增量之比是∶∶
【解析】 水平发射的弹丸做平抛运动,竖直方向上是自由落体运动,水平方向上是匀速直线运动。又因为竖直方向上Oa=ab=bc,即Oa∶Ob∶Oc=1∶2∶3,由h=gt2可知ta∶tb∶tc=1∶∶,由水平方向x=v0t可得va∶vb∶vc=1∶∶=∶∶,故选项A正确,B错误;由Δv=gt,可知从射出至打到墙上过程速度增量之比是1∶∶,故选项C正确,D错误。
【答案】 AC
考法(三) 落点在圆弧面上的平抛运动
3.如图所示,水平路面出现了一个大坑,其竖直截面为半圆,AB为沿水平方向的直径。一辆行驶的汽车发现情况后紧急刹车安全停下,但两颗石子分别以速度v1、v2从A点沿AB方向水平飞出,分别落于C、D两点,C、D两点距水平路面距离分别为圆半径的0.6倍和1倍。则v1∶v2的值为( )
A. B.
C. D.
【解析】 设圆弧的半径为R,依平抛运动规律得x1=v1t1,x2=v2t2,
联立得===。
时间由竖直方向做自由落体运动来比较,y1=gt12,y2=gt22,
由两式相比得=,其中y1=R,y2=R,
则有= ,代入速度公式得=,C项正确。
【答案】 C
【题型技法】
落点在圆弧面上的三种常见情景
(1)如图甲所示,小球从半圆弧左边沿平抛,落到半圆内的不同位置。由半径和几何关系制约时间t:h=gt2,R±=v0t,联立两方程可求t。
(2)如图乙所示,小球恰好沿B点的切线方向进入圆轨道,此时半径OB垂直于速度方向,圆心角α与速度的偏向角相等。
(3)如图丙所示,小球恰好从圆柱体Q点沿切线飞过,此时半径OQ垂直于速度方向,圆心角θ与速度的偏向角相等。
考法(四) 落点在水平台阶上的平抛运动
4.一阶梯如图所示,其中每级台阶的高度和宽度都是0.4 m。一小球以水平速度v飞出,g取10 m/s2,欲打在第四级台阶上,则v的取值范围是( )
A. m/s
考点四 四类常见平抛运动模型
模型一 水平地面上空h处的平抛运动
由h=gt2知t=,即t由高度h决定.
模型二 半圆内的平抛运动(如图甲)
由半径和几何关系制约时间t:
h=gt2
R±=v0t
联立两方程可求t.
模型三 斜面上的平抛运动
1.顺着斜面平抛(如图乙)
方法:分解位移
x=v0t
y=gt2
tan θ=可求得t=
2.对着斜面平抛(如图丙)
方法:分解速度
vx=v0
vy=gt
tan θ==
可求得t=
模型四 对着竖直墙壁的平抛运动(如图丁)
水平初速度v0不同时,虽然落点不同,但水平位移相同.t=
1.如图,从半径为R=1 m的半圆AB上的A点水平抛出一个可视为质点的小球,经t=0.4 s小球落到半圆上.已知当地的重力加速度g=10 m/s2,则小球的初速度v0可能为( )
A.1 m/s B.2 m/s
C.3 m/s D.4 m/s
【解析】 由于小球经0.4 s落到半圆上,下落的高度h=gt2=0.8 m,位置可能有两处,如图所示.
第一种可能:小球落在半圆左侧,v0t=R-=0.4 m,v0=1 m/s
第二种可能:小球落在半圆右侧,
v0t=R+,v0=4 m/s,选项A、D正确.
【答案】 AD
2.如图所示,斜面上有a、b、c、d四个点,ab=bc=cd.从a点正上方的O点以速度v水平抛出一个小球,它落在斜面上b点.若小球从O点以速度2v水平抛出,不计空气阻力,则它落在斜面上的( )
A.b与c之间某一点 B.c点
C.c与d之间某一点 D.d点
【解析】 如图所示,过b点做水平线be,由题意知小球第一次落在b点,第二次速度变为原来的2倍后,轨迹为Oc′,c′在c的正下方be线上,故轨迹与斜面的交点应在bc之间.据运动规律作图越直观,对解决问题越有利.
【答案】 A
【考能提升·对点演练】
1.从同一水平直线上的两位置分别沿同方向抛出两小球A和B,其运动轨迹如图所示,不计空气阻力.要使两球在空中相遇,则必须( )
A.两球的初速度一样大
B.B球初速度比A大
C.同时抛出两球
D.先抛出A球
【解析】 小球在竖直方向上做自由落体运动,由h=gt2,两小球从同一高度抛出在空中某处相遇,则两小球下落时间相同,故说明两小球从同一时刻抛出,C正确,D错误;由x=v0t,A球的水平位移大,说明A的初速度大,A、B错误.
【答案】 C
2.(多选)在地面上方高为H处某点将一小球水平抛出,不计空气阻力,则小球在随后(落地前)的运动中( )
A.初速度越大,小球落地的瞬时速度与竖直方向的夹角越大
B.初速度越大,落地瞬间小球重力的瞬时功率越大
C.初速度越大,在相等的时间间隔内,速度的改变量越大
D.无论初速度为何值,在相等的时间间隔内,速度的改变量总是相同的
【解析】选AD 设小球落地瞬间速度的方向与竖直方向的夹角为α,根据tan α==知,初速度越大,小球落地瞬间速度与竖直方向的夹角越大,故A正确。根据P=mgvy=mg知,落地时小球重力的瞬时功率与初速度无关,故B错误。平抛运动的加速度不变,在相等的时间间隔内速度的改变量相同,与初速度无关,故C错误,D正确。
【答案】 AD
3.一阶梯如图所示,其中每级台阶的高度和宽度都是0.4 m,一小球以水平速度v飞出,g取10 m/s2,欲打在第四台阶上,则v的取值范围是( )
A. m/s
4.如图所示,在同一平台上的O点水平抛出的三个物体,分别落到a、b、c三点,则三个物体运动的初速度va、vb、vc和运动的时间ta、tb、tc的关系分别是( )
A.va>vb>vc ta>tb>tc B.va
5.如图所示,一小球从一半圆轨道左端A点正上方某处开始做平抛运动(小球可视为质点),飞行过程中恰好与半圆轨道相切于B点.O为半圆轨道圆心,半圆轨道半径为R,OB与水平方向夹角为60°,重力加速度为g,则小球抛出时的初速度为( )
A. B.
C. D.
【解析】 画出小球在B点速度的分解矢量图.由图可知,tan 60°=,R(1+cos 60°)=v0t,联立解得:v0=,选项B正确.
【答案】 B
6.如图,斜面AC与水平方向的夹角为α,在A点正上方与C等高处水平抛出一小球,其速度垂直于斜面落到D点,则CD与DA的比为( )
A. B.
C. D.
【解析】选D 设小球水平方向的速度为v0,将D点的速度进行分解,水平方向的速度等于平抛运动的初速度,通过几何关系求解,得竖直方向的末速度为v2=,设该过程用时为t,则DA间水平距离为v0t,故DA=;CD间竖直距离为,故CD=,得=,故D正确。
【答案】 D
7.根据高中所学知识可知,做自由落体运动的小球,将落在正下方位置。但实际上,赤道上方200 m处无初速下落的小球将落在正下方位置偏东约6 cm 处。这一现象可解释为,除重力外,由于地球自转,下落过程小球还受到一个水平向东的“力”,该“力”与竖直方向的速度大小成正比。现将小球从赤道地面竖直上抛,考虑对称性,上升过程该“力”水平向西,则小球( )
A.到最高点时,水平方向的加速度和速度均为零
B.到最高点时,水平方向的加速度和速度均不为零
C.落地点在抛出点东侧
D.落地点在抛出点西侧
【解析】选D 将小球的竖直上抛运动分解为水平方向和竖直方向的两个分运动。上升阶段,随着小球竖直分速度的减小,其水平向西的“力”逐渐减小,因此水平向西的加速度逐渐减小,到最高点时减小为零,而水平向西的速度达到最大值,故A、B错误。下降阶段,随着小球竖直分速度的变大,其水平向东的“力”逐渐变大,水平向东的加速度逐渐变大,小球的水平分运动是向西的变减速运动,根据对称性,小球落地时水平向西的速度减小为零,所以落地点在抛出点西侧,故C错误、D正确。
【答案】 D
8.如图所示,在距地面高为H=45 m处,有一小球A以初速度v0=10 m/s水平抛出,与此同时,在A的正下方有一物块B也以相同的初速度同方向滑出,B与水平地面间的动摩擦因数为μ=0.4,A、B均可视为质点,空气阻力不计(取g=10 m/s2).下列说法正确的是( )
A.小球A落地时间为3 s B.物块B运动时间为3 s
C.物块B运动12.5 m后停止 D.A球落地时,A、B相距17.5 m
【解析】 根据H=gt2得,t= = s=3 s,故A正确;物块B匀减速直线运动的加速度大小a=μg=0.4×10 m/s2=4 m/s2,则B速度减为零的时间t0== s=2.5 s,滑行的距离x=t0=×2.5 m=12.5 m,故B错误,C正确;A落地时,A的水平位移xA=v0t=10×3 m=30 m,B的位移xB=x=12.5 m,则A、B相距Δx=(30-12.5)m=17.5 m,故D正确.
【答案】 ACD
9.在一斜面顶端,将甲、乙两个小球分别以v和的速度沿同一方向水平抛出,两球都落在该斜面上。甲球落至斜面时的速率是乙球落至斜面时速率的( )
A.2倍 B.4倍
C.6倍 D.8倍
【解析】选A 画出小球在斜面上运动轨迹,如图所示,可知:
x=vt,
x·tan θ=gt2
则x=·v2,
即x∝v2
甲、乙两球抛出速度为v和,则相应水平位移之比为4∶1,由相似三角形知,下落高度之比也为4∶1,由自由落体运动规律得,落在斜面上竖直方向速度之比为2∶1,由落至斜面时的速率v斜=可得落至斜面时速率之比为2∶1。
【答案】 A
10.飞镖运动于十五世纪兴起于英格兰,二十世纪初,成为人们日常休闲的必备活动.一般打飞镖的靶上共标有10环,第10环的半径最小.现有一靶的第10环的半径为1 cm,第9环的半径为2 cm……以此类推,若靶的半径为10 cm,在进行飞镖训练时,当人离靶的距离为5 m,将飞镖对准第10环中心以水平速度v投出,g=10 m/s2.则下列说法中正确的是( )
A.当v≥50 m/s时,飞镖将射中第8环线以内
B.当v=50 m/s时,飞镖将射中第6环线
C.若要击中第10环的线内,飞镖的速度v至少为50 m/s
D.若要击中靶子,飞镖的速度v至少为25 m/s
【解析】 根据平抛运动规律可得,飞镖在空中飞行有:x=vt,h=gt2,将第8环半径为3 cm、第6环半径为5 cm、第10环半径为1 cm、靶的半径为10 cm代入两式可知正确选项为B、D.
【答案】 BD
11.如图所示,A、B两球用两段不可伸长的细绳连接于悬点O,两段细绳的长度之比为1∶2。现让两球同时从悬点O处以一定的初速度分别向左、向右水平抛出,至连接两球的细绳伸直所用时间之比为1∶。若两球的初速度大小的比值=k,则k应满足的条件是( )
A.k= B.k>
C.k= D.k>
【解析】选A 设与A、B两球相连的绳的长度分别为l和2l,当与A球相连的绳绷直时,
有x=vAt,y=gt2,
x2+y2=l2,解得vA=,
同理对B球有vB=,
求得k==,A正确。
【答案】 A
12.为了验证平抛运动的小球在竖直方向上做自由落体运动,用如图所示的装置进行实验.小锤打击弹性金属片,A球水平抛出,同时B球被松开,自由下落.关于该实验,下列说法中正确的有( )
A.两球的质量应相等
B.两球应同时落地
C.应改变装置的高度,多次实验
D.实验也能说明A球在水平方向上做匀速直线运动
【解析】 小锤打击弹性金属片后,A球做平抛运动,B球做自由落体运动.A球在竖直方向上的运动情况与B球相同,做自由落体运动,因此两球同时落地.实验时,需A、B两球从同一高度开始运动,对质量没有要求,但两球的初始高度及击打力度应该有变化,实验时要进行3~5次得出结论.本实验不能说明A球在水平方向上的运动性质,故选项B、C正确,选项A、D错误.
【答案】 BC
13.如图所示,一名运动员在参加跳远比赛,他腾空过程中离地面的最大高度为L,成绩为4L。假设跳远运动员落入沙坑瞬间速度方向与水平面的夹角为α,运动员可视为质点,不计空气阻力,则有( )
A.tan α=2 B.tan α=1
C.tan α= D.tan α=
【解析】选B 腾空过程中离地面的最大高度为L,从最高点到落地过程中,做平抛运动,根据平抛运动规律,L=gt2,解得:t= ,运动员在空中最高点的速度即为运动员起跳时水平方向的分速度,根据分运动与合运动的等时性,则水平方向的分速度为:vx==,根据运动学公式,在最高点竖直方向速度为零,那么运动员落到地面时的竖直分速度为:vy=gt=,运动员落入沙坑瞬间速度方向与水平面的夹角的正切值为:tan α===1,故B正确,A、C、D错误。
【答案】 B
14.据悉,我国已在陕西省西安市的阎良机场建立了一座航空母舰所使用的滑跳式甲板跑道,用来让飞行员练习在航空母舰上的滑跳式甲板起飞。如图所示的AOB为此跑道纵截面示意图,其中AO段水平,OB为抛物线,O点为抛物线的顶点,抛物线过O点的切线水平,OB的水平距离为x,竖直高度为y。某次训练中,观察战机(视为质点)通过OB段时,得知战机在水平方向做匀速直线运动,所用时间为t,则战机离开B点的速率为( )
A. B.
C. D.
【解析】选D 战机的运动轨迹是抛物线,当水平方向做匀速直线运动时,竖直方向做初速度为零的匀加速直线运动,则战机到达B点时的水平分速度大小vx=,竖直分速度大小vy=,合速度大小为v==,选项D正确。
【答案】 D
15.如图所示为足球球门,球门宽为L.一个球员在球门中心正前方距离球门s处高高跃起,将足球顶入球门的左下方死角(图中P点).球员顶球点的高度为h.足球做平抛运动(足球可看成质点,忽略空气阻力),则( )
A.足球位移的大小x=
B.足球初速度的大小v0=
C.足球末速度的大小v=
D.足球初速度的方向与球门线夹角的正切值tanθ=
【解析】 足球位移大小为x==,A错误;根据平抛运动规律有:h=gt2, =v0t,解得v0=,B正确;根据动能定理mgh=mv2-mv可得v==,C错误;足球初速度方向与球门线夹角正切值tan θ==,D错误.
【答案】 B
16.如图,圆弧形凹槽固定在水平地面上,其中ABC是位于竖直平面内以O为圆心的一段圆弧,OA与竖直方向的夹角为α.一小球以速度v0从桌面边缘P水平抛出,恰好从A点沿圆弧的切线方向进入凹槽.小球从P到A的运动时间为 ________ ;直线PA与竖直方向的夹角β= ________ .
【解析】 据题意,小球从P点抛出后做平抛运动,小球运动到A点时将速度分解,有tan α==,则小球运动到A点的时间为:t=;从P点到A点的位移关系有:tan β====2cot α,所以PA与竖直方向的夹角为:β=arctan(2cot α).
【答案】 arctan(2cot α)
17.风洞实验室能产生大小和方向均可改变的风力。如图所示,在风洞实验室中有足够大的光滑水平面,在水平面上建立xOy直角坐标系。质量m=0.5 kg的小球以初速度v0=0.40 m/s从O点沿x轴正方向运动,在0~2.0 s内受到一个沿y轴正方向、大小F1=0.20 N的风力作用;小球运动2.0 s后风力方向变为沿y轴负方向、大小变为F2=0.10 N(图中未画出)。试求:
(1)2.0 s末小球在y轴方向的速度大小和2.0 s内运动的位移大小;
(2)风力F2作用多长时间,小球的速度变为与初速度相同。
【解析】(1)设在0~2.0 s内小球运动的加速度为a1,
则F1=ma1
2.0 s末小球在y轴方向的速度v1=a1t1
代入数据解得v1=0.8 m/s
沿x轴方向运动的位移x1=v0t1
沿y轴方向运动的位移y1=a1t12
2.0 s内运动的位移s1=
代入数据解得s1=0.8 m≈1.1 m。
(2)设2.0 s后小球运动的加速度为a2,F2的作用时间为t2时小球的速度变为与初速度相同,则F2=ma2
0=v1-a2t2
代入数据解得t2=4.0 s。
【答案】(1)0.8 m/s 1.1 m (2)4.0 s
18.如图所示,倾角为37°的斜面长l=1.9 m,在斜面底端正上方的O点将一小球以v0=3 m/s的速度水平抛出,与此同时静止释放顶端的滑块,经过一段时间后小球恰好能够以垂直斜面的方向击中滑块.(小球和滑块均可视为质点,重力加速度g取10 m/s2,sin 37°=0.6,cos 37°=0.8),求:
(1)抛出点O离斜面底端的高度;
(2)滑块与斜面间的动摩擦因数μ.
【解析】 (1)设小球击中滑块时的竖直速度为vy,由几何关系得=tan 37°
设小球下落的时间为t,竖直位移为y,水平位移为x,由运动学规律得
vy=gt,y=gt2,x=v0t
设抛出点到斜面最低点的距离为h,由几何关系得
h=y+xtan 37°
由以上各式得h=1.7 m.
(2)在时间t内,滑块的位移为x′,由几何关系得
x′=l-,
设滑块的加速度为a,由运动学公式得x′=at2,
对滑块由牛顿第二定律得
mgsin 37°-μmgcos 37°=ma,
由以上各式得μ=0.125.
【答案】 (1)1.7 m (2)0.125
19.用如图甲所示的水平—斜面装置研究平抛运动。一物块(可视为质点)置于粗糙水平面上的O点,O点与斜面顶端P点的距离为s。每次用水平拉力F,将物块由O点从静止开始拉动,当物块运动到P点时撤去拉力F。实验时获得物块在不同拉力作用下落在斜面上的不同水平射程,作出了如图乙所示的图像。若物块与水平面间的动摩擦因数为0.5,斜面与水平地面之间的夹角θ=45°,g取10 m/s2,设最大静摩擦力等于滑动摩擦力。求O、P间的距离s。(保留两位有效数字)
【解析】根据牛顿第二定律,在OP段有F-μmg=ma,
又2as=vP2,
由平抛运动规律和几何关系有
物块的水平射程x=vPt,
物块的竖直位移y=gt2,
由几何关系有y=xtan θ,
联立以上各式可以得到x=,
解得F= x+μmg。
由题图乙知μmg=5,=10,
代入数据解得s=0.25 m。
【答案】0.25 m
第1节 功和功率-2023年高考物理二轮复习对点讲解与练习(通用版): 这是一份第1节 功和功率-2023年高考物理二轮复习对点讲解与练习(通用版),文件包含第1节功和功率解析版docx、第1节功和功率原卷版docx、第1节电磁感应现象楞次定律解析版docx、第1节电磁感应现象楞次定律原卷版docx等4份试卷配套教学资源,其中试卷共70页, 欢迎下载使用。
第2节 摩擦力-2023年高考物理二轮复习对点讲解与练习(通用版): 这是一份第2节 摩擦力-2023年高考物理二轮复习对点讲解与练习(通用版),文件包含第2节摩擦力解析版doc、第2节摩擦力原卷版doc等2份试卷配套教学资源,其中试卷共26页, 欢迎下载使用。
第2节 动能、动能定理-2023年高考物理二轮复习对点讲解与练习(通用版): 这是一份第2节 动能、动能定理-2023年高考物理二轮复习对点讲解与练习(通用版),文件包含第2节动能动能定理解析版docx、第2节动能动能定理原卷版docx等2份试卷配套教学资源,其中试卷共36页, 欢迎下载使用。












