高考数学一轮复习第5章5.3平面向量的数量积与平面向量的应用课件

这是一份高考数学一轮复习第5章5.3平面向量的数量积与平面向量的应用课件，共41页。PPT课件主要包含了内容索引，必备知识预案自诊，知识梳理，向量的夹角，a⊥b，常用结论，考点自诊，答案D，答案ABC，答案A等内容，欢迎下载使用。

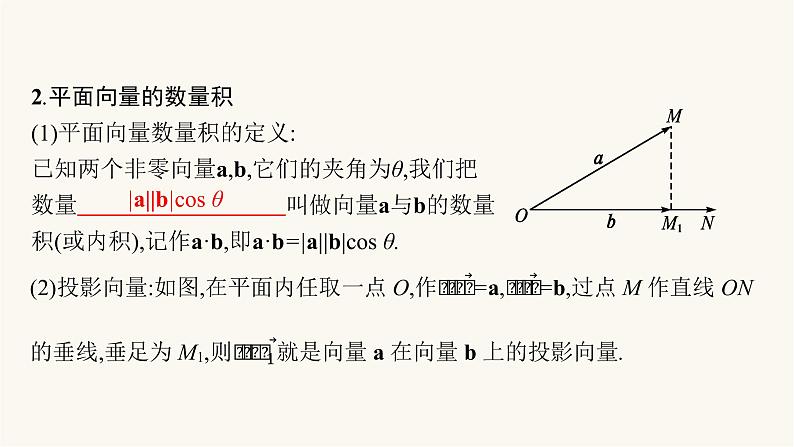
2.平面向量的数量积(1)平面向量数量积的定义:已知两个非零向量a,b,它们的夹角为θ,我们把数量　　　　　　　　　叫做向量a与b的数量积(或内积),记作a·b,即a·b=|a||b|cs θ. 
|a||b|cs θ
3.向量数量积的运算律
4.平面向量数量积的性质及坐标表示已知非零向量a=(x1,y1),b=(x2,y2),a与b的夹角为θ.
5.向量在平面几何中的应用
1.平面向量数量积运算的常用公式:(1)(a+b)·(a-b)=a2-b2.(2)(a±b)2=a2±2a·b+b2.2.当a与b同向时,a·b=|a||b|;当a与b反向时,a·b=-|a||b|.3.a与b的夹角θ为锐角,则有a·b>0,反之不成立(θ为0时不成立);a与b的夹角为钝角,则有a·b<0,反之不成立(θ为π时不成立).
1.判断下列结论是否正确,正确的画“√”,错误的画“×”.
(2)若a·b>0,则a和b的夹角为锐角;若a·b<0,则a和b的夹角为钝角.(　　)(3)若a·b=0,则必有a⊥b.(　　)(4)(a·b)·c=a·(b·c).(　　)(5)若a·b=a·c(a≠0),则b=c.(　　)
2.已知向量a,b满足a·(b+a)=2,且a=(1,2),与a方向相同的单位向量为e,则向量b在向量a上的投影向量为(　　)
3.(多选)(2020海南三亚华侨学校高三模考)已知a=(3,-1),b=(1,-2),则正确的有(　　)A.a·b=5D.a与b平行
A.(-2,6)B.(-6,2)C.(-2,4)D.(-4,6)
答案 (1)-1　(2)A　解析 (1)∵AD∥BC,且∠DAB=30°,∴∠ABE=30°.∵EA=EB,∴∠EAB=30°,∠AEB=120°.在△AEB中,EA=EB=2,
解题心得1.求两个向量的数量积的方法:(1)当已知向量的模和夹角时,利用定义求解,即a·b=|a||b|cs θ(其中θ是向量a与b的夹角).(2)当已知向量的坐标时,可利用坐标法求解,即若a=(x1,y1),b=(x2,y2),则a·b=x1x2+y1y2.2.解决涉及几何图形的向量数量积运算问题时,可利用向量的加、减、数量积的运算律化简.但一定要注意向量的夹角与已知平面角的关系是相等还是互补.
考向1　求平面向量的模【例2】 (1)已知平面向量a,b,|a|=1,|b|=2,a⊥(a-2b),则|2a+b|的值是　　　　. 
考向2　求平面向量的夹角
答案 (1)D　(2)B　解析 (1)∵a·(a+b)=a2+a·b=25-6=19,|a+b|2=a2+b2+2a·b=25+36-12=49,∴|a+b|=7,(2)因为(a-b)⊥b,所以(a-b)·b=a·b-b2=0,所以a·b=b2.
考向3　平面向量的垂直【例4】 (1)(2020全国2,理13)已知单位向量a,b的夹角为45°,ka-b与a垂直,则k=　　　　　. 
解题心得1.求向量的模的方法:(1)公式法,利用 及(a±b)2=|a|2±2a·b+|b|2,把向量的模的运算转化为数量积运算;(2)几何法,利用向量的几何意义求解.2.求向量模的最值(范围)的方法:(1)代数法,把所求的模表示成某个变量的函数,再用求最值的方法求解;(2)几何法(数形结合法),弄清所求的模表示的几何意义,结合动点表示的图形求解.3.已知两个向量的垂直关系,求解相关参数的值根据两个向量垂直的充要条件,列出相应的关系式,进而求解参数.
对点训练2(1)(2020福建厦门一模)已知a=(1,1),b=(2,m),a⊥(a-b),则|b|=(　　)A.0B.1C. D.2(2)(2020全国1,文14)设向量a=(1,-1),b=(m+1,2m-4),若a⊥b,则m=　　　　　. 
答案 (1)D　(2)5　解析 (1)由题意知a-b=(-1,1-m),∵a⊥(a-b),∴a·(a-b)=-1+1-m=0,∴m=0,∴b=(2,0),∴|b|=2.故选D.(2)由a⊥b,可得a·b=1×(m+1)+(-1)×(2m-4)=0,解得m=5.
考向1　平面向量在三角函数中的应用【例5】 已知向量a=(cs x,sin x),b=(3,- ),x∈[0,π].(1)若a∥b,求x的值;(2)记f(x)=a·b,求f(x)的最大值和最小值以及对应的x的值.
解题心得向量与三角函数综合问题的特点与解题策略(1)以向量为载体考查三角函数的综合应用题目,通过向量的坐标运算构建出三角函数,然后再考查有关三角函数的最值、单调性、周期性等三角函数性质问题,有时还加入参数,考查分类讨论的思想方法.(2)向量与三角函数结合时,通常以向量为表现形式,实现三角函数问题,所以要灵活运用三角函数中的相关方法与技巧求解.
考向2　平面向量在解析几何中的应用【例6】 已知圆x2+y2+4x-5=0的弦AB的中点为(-1,1),直线AB交x轴于点P,则 的值为　　　　　. 
解题心得1.数量积大于0说明不共线的两个向量的夹角为锐角;数量积等于0说明不共线的两个向量的夹角为直角;数量积小于0说明不共线的两个向量的夹角为钝角.2.若a,b为非零向量,cs θ= (夹角公式),则a⊥b⇔a·b=0.3.向量在解析几何中的作用(1)载体作用:解决向量在解析几何中的应用问题的关键是利用向量的意义、运算脱去“向量外衣”,导出曲线上点的坐标之间的关系,从而解决有关距离、斜率、夹角、轨迹、最值等问题.(2)工具作用:利用数量积与共线定理可解决垂直、平行问题.特别地,向量垂直、平行的坐标表示对于解决解析几何中的垂直、平行问题是一种比较可行的方法.