高中数学人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.3 对数教学演示课件ppt

这是一份高中数学人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.3 对数教学演示课件ppt，共26页。PPT课件主要包含了新知初探·课前预习，0＋∞，－∞0，y＝ax，答案A，1＋∞，题型探究·课堂解透，答案B，答案C，ba1dc等内容，欢迎下载使用。

课程标准(1)理解对数函数的概念，会求对数函数的定义域．(2)能画出具体对数函数的图象，并能根据对数函数的图象说明对数函数的性质．
教 材 要 点要点一　对数函数的概念一般地，把函数y＝lgax(a>0，且a≠1)叫做对数函数，其中x是自变量，函数的定义域是________❶.
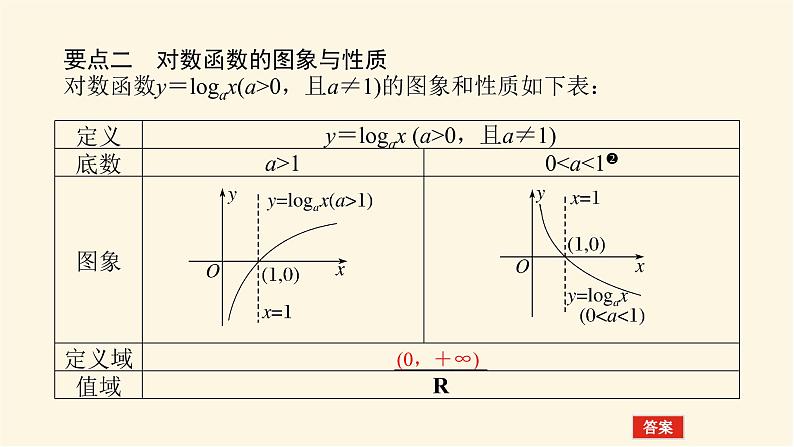
要点二　对数函数的图象与性质对数函数y＝lgax(a>0，且a≠1)的图象和性质如下表：
要点三　反函数指数函数______(a>0，且a≠1)与对数函数y＝______________互为反函数❸.
lgax(a>0且a≠1)
助 学 批 注批注❶　由指数式与对数式的关系知，对数函数的自变量x恰好是指数函数的函数值y，所以对数函数的定义域是(0，＋∞)．批注❷　底数a与1的大小关系决定了对数函数图象的“升降”：当a＞1时，对数函数的图象“上升”；当0＜a＜1时，对数函数的图象“下降”．批注❸　图象关于直线y＝x对称．
基 础 自 测1．思考辨析(正确的画“√”，错误的画“×”)(1)y＝lg2x2是对数函数．(　　)(2)对数函数的图象一定在y轴的右侧．(　　)(3)函数y＝lga(x＋1)的定义域为(0，＋∞)．(　　)(4)函数y＝lg2x与y＝x2互为反函数．(　　)
解析：设函数解析式为y＝lgax(a>0，且a≠1)．由于对数函数的图象过点M(125，3)，所以3＝lga125，得a＝5.所以对数函数的解析式为y＝lg5x.
解析：由图可知，a>1.
4．函数f(x)＝lg0.5(x－1)的定义域是________．
解析：要使函数f(x)＝lg0.5(x－1)有意义就要x－1>0，即x>1，所以函数f(x)＝lg0.5(x－1)的定义域是(1，＋∞)．
题型 1　对数函数的概念例1　(1)指出下列函数是对数函数的是(　　)A．y＝3lg2x B．y＝lg6xC．y＝lgx3 D．y＝lg2x＋1
解析：A中lg2x的系数是3，不是1，不是对数函数．B符合对数函数的结构形式，是对数函数．C中自变量在底数位置上，不是对数函数．D中对数式lg2x后又加1，不是对数函数．
方法归纳判断一个函数是对数函数的方法
巩固训练1　已知函数f(x)＝(2m2－m)lgax＋m－1是对数函数，则m＝________．
题型 2　对数型函数的定义域例2　求下列函数的定义域．(1)y＝lga(3－x)＋lga(3＋x)；(2)y＝lg2(16－4x)．(3)f(x)＝lg(2x－1)(－4x＋8)．
方法归纳求对数型函数的方法除遵循前面已学习过的求函数定义域的方法外，还要对这种函数自身有如下要求：一是要特别注意真数大于零；二是要注意对数的底数大于零且不等于1.
题型 3 对数函数的图象例3　(1)如图所示的曲线是对数函数y＝lgax，y＝lgbx，y＝lgcx，y＝lgdx的图象，则a，b，c，d与1的大小关系为___________．
解析：由题图可知函数y＝lgax，y＝lgbx的底数a＞1，b＞1，函数y＝lgcx，y＝lgdx的底数0＜c＜1，0＜d＜1.过点(0，1)作平行于x轴的直线，则直线与四条曲线交点的横坐标从左向右依次为c，d，a，b，显然b＞a＞1＞d＞c.
(2)已知函数y＝lga(x＋3)－1(a＞0，且a≠1)的图象恒过定点A，若点A也在函数f(x)＝3x＋b的图象上，则f(lg32)＝________． 
方法归纳解与对数函数图象有关问题的策略
巩固训练3　(1)函数y＝lg (x＋1)的图象大致是(　　)
解析：由底数大于1可排除A、B，y＝lg (x＋1)可看作是y＝lg x的图象向左平移1个单位．(或令x＝0得y＝0，而且函数为增函数)．