人教B版 (2019)必修 第二册4.3 指数函数与对数函数的关系教学课件ppt

这是一份人教B版 (2019)必修 第二册4.3 指数函数与对数函数的关系教学课件ppt，共31页。PPT课件主要包含了新知初探·自主学习，任意一个y的值，唯一的x，定义域，0＋∞，减函数，增函数，答案D，答案B，课堂探究·素养提升等内容，欢迎下载使用。
【课程标准】(1)了解反函数的定义．(2)了解指数函数与对数函数互为反函数．
教 材 要 点知识点一　反函数的定义(1)定义：如果在函数y＝f(x)中，给定值域中_____________，只有________与之对应，那么x是y的函数，这个函数称为y＝f(x)的反函数．(2)记法：y＝f－1(x).
状元随笔　1.函数f(x)＝x2有反函数吗？为什么？提示：没有．若令y＝f(x)＝1，则x＝±1，即x值不唯一，不符合反函数的定义．2．什么样的函数一定有反函数？提示：单调函数．
知识点二　反函数的求法对调y＝f(x)中的x与y，然后从x＝f(y)中求出y得到．知识点三　函数与其反函数的性质的关系(1)图象：关于直线y＝x对称；(2)定义域、值域：原函数的________与其反函数的________相同；原函数的________与其反函数的________相同．(3)单调性：原函数与其反函数的单调性________．
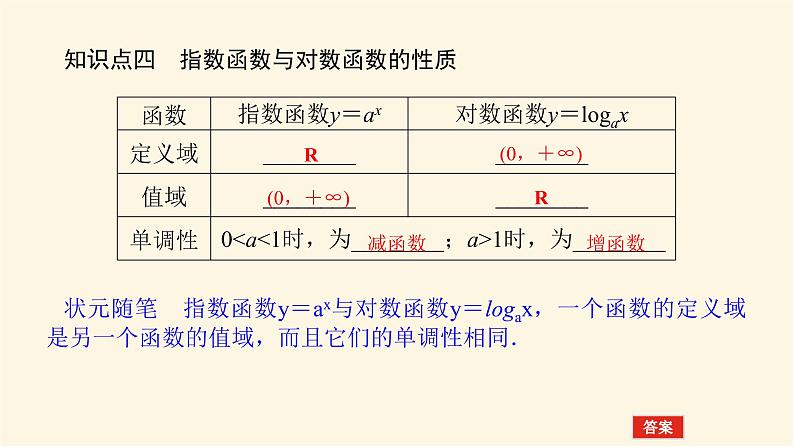
知识点四　指数函数与对数函数的性质状元随笔　指数函数y＝ax与对数函数y＝lgax，一个函数的定义域是另一个函数的值域，而且它们的单调性相同．
基 础 自 测1．函数f(x)＝lg4x与g(x)＝4x的图象(　　)A．关于x轴对称　 B．关于y轴对称C．关于原点对称　　 D．关于直线y＝x对称
解析：∵g(x)＝22x＝4x，∴函数f(x)＝lg4x与g(x)＝22x互为反函数，它们的图象关于直线y＝x对称．
解析：由于函数y＝f(x)是函数y＝ax(a>0且a≠1)的反函数，则f(x)＝lgax，则f(2)＝lga2＝1，解得a＝2，因此，f(x)＝lg2x.
3．若函数f(x)＝2x的反函数为f－1(x)，则f－1(1)＝________．
解析：令2x＝1，则x＝0，所以f－1(1)＝0.
4．若函数y＝f(x)的图象位于第一、二象限，则它的反函数y＝f－1(x)的图象位于(　　)A．第一、二象限　 B．第三、四象限C．第二、三象限　　 D．第一、四象限
解析：结合函数与反函数关于y＝x对称得出，即可得出反函数位于第一、四象限．
题型1　判断函数是否有反函数(逻辑推理)例1　下列函数中，存在反函数的是(　　)A． B． C． D．
【解析】　对A，因为f(x)＝1时，x为任意的正实数，即对应的x不唯一，因此f(x)的反函数不存在；对B，因为g(x)＝1时，x为任意的有理数，即对应的x不唯一，因此g(x)的反函数不存在；对C，因为h(x)＝2时，x＝2或x＝5，即对应的x不唯一，因此h(x)的反函数不存在；对D，因为l(x)的值域为{－2，－1，0，3，4}中任意一个值，都只有唯一的x与之对应，因此l(x)的反函数存在．
方法归纳判定函数存在反函数的方法(1)逐一考查值域中函数值对应的自变量的取值，如果都是唯一的，则函数的反函数存在．(2)确定函数在定义域上的单调性，如果函数是单调函数，则函数的反函数存在．(3)利用原函数的解析式，解出自变量x，如果x是唯一的，则函数的反函数存在．
1．判断函数是否单调．2．求出x.3．推导出f －1(x)的解析式．
方法归纳求给定解析式的函数的反函数的步骤(1)求出原函数的值域，这就是反函数的定义域；(2)从y＝f(x)中解出x；(3)x，y互换并注明反函数的定义域．
1．函数在定义域内的值域．2．求x.3．解出f －1(x).
题型3　反函数性质的应用例3　(1)已知函数y＝ax＋b的图象过点(1，4)，其反函数的图象过点(2，0)，求a，b的值．
函数与反函数图象上相应点关于y＝x对称．
反函数的自变量值即原函数的函数值．
方法归纳利用反函数的性质解题互为反函数的图象关于直线y＝x对称是反函数的重要性质，由此可得互为反函数图象上任一成对的相应点也关于y＝x对称，所以若点 (a，b)在函数y＝f(x)的图象上，则点(b，a)必在其反函数y＝f－1(x)的图象上．
跟踪训练3　(1)已知函数f(x)＝ax＋b(a>0且a≠1)的图象过点(1，7)，其反函数f－1(x)的图象过点(4，0)，求f(x)的表达式．
解析：∵y＝f－1(x)的图象过点(4，0)，∴y＝f(x)的图象过点(0，4)，∴1＋b＝4，∴b＝3，又∵f(x)＝ax＋b的图象过点(1，7)，∴a＋b＝7，∴a＝4.∴f(x)＝4x＋3.
(2)已知函数f(x)＝1＋2lg x，则f(1)＋f－1(1)＝(　　)A．0　　　B．1 C．2　　　D．3
解析：根据题意：f(1)＝1＋2lg 1＝1，若f(x)＝1＋2lg x＝1，解得x＝1，则f－1(1)＝1，故f(1)＋f－1(1)＝1＋1＝2.
题型4　指数函数与对数函数图象间的关系例4　已知lg a＋lg b＝0，函数f(x)＝ax与函数g(x)＝－lgbx的图象可能是(　　)
(1)由lg a＋lg b＝0得ab＝1.(2)f(x)与y(x)互为反函数．
方法归纳利用反函数的性质识图指数函数与对数函数互为反函数，二者的图象关于直线y＝x对称，在有关指数函数与对数函数的图象知识问题中利用这一性质，结合平移翻转等可以很方便地解决问题．
跟踪训练4　y＝lg2x的反函数是y＝f－1(x)，则函数y＝f－1(1－x)的图象是下图中的(　　)
状元随笔　1.先求出f －1(x).2．再求f －1(－x).3．最后求出f －1(1－x).