高中数学湘教版（2019）必修 第一册5.3 三角函数的图象与性质说课课件ppt

这是一份高中数学湘教版（2019）必修 第一册5.3 三角函数的图象与性质说课课件ppt，共39页。PPT课件主要包含了新知初探课前预习，最小正周期，答案D，答案A，题型探究课堂解透，答案B，易错警示，答案ABC等内容，欢迎下载使用。

要点一　周期函数1．周期函数一般地，对于函数y＝f(x)，如果存在________常数T，使得当x取定义域内每一个值时，x±T都有定义，并且__________，则称这个函数y＝f(x)为周期函数，T称为这个函数的一个周期．
f(x±T)＝f(x)
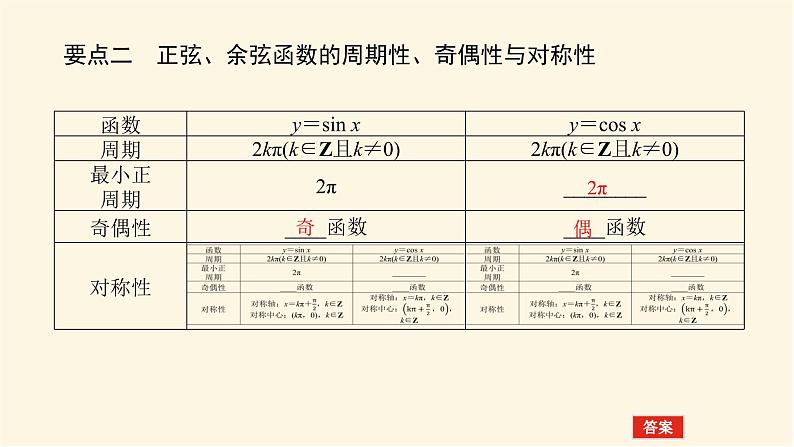
要点二　正弦、余弦函数的周期性、奇偶性与对称性
状元随笔　(1)正弦函数是奇函数，余弦函数是偶函数，反映在图象上，正弦曲线关于原点(0，0)对称，余弦曲线关于y轴对称．(2)正弦曲线、余弦曲线既是中心对称图形又是轴对称图形．
3．函数f(x)＝sin (－x)的奇偶性是(　　)A．奇函数 B．偶函数C．既是奇函数又是偶函数 D．非奇非偶函数
解析：由于x∈R，且f(－x)＝sin x＝－sin (－x)＝－f(x)，所以f(x)为奇函数，故选A.
4．函数f(x)＝sin x cs x是________函数．(填“奇”或“偶”)
解析：∵f(x)＝sin x cs x，且x∈R∴f(－x)＝sin (－x)cs (－x)＝－sin x cs x＝－f(x)，∴f(x)＝sin x cs x是奇函数．
答案：(1)C　(2)见解析
方法归纳 判断函数奇偶性的两个关键点(1)看函数的定义域是否关于原点对称；(2)看f(－x)与f(x)的关系．对于三角函数奇偶性的判断，有时可根据诱导公式先将函数式化简后再判断．
跟踪训练2　函数f(x)＝|sin x|＋cs x是(　　)A．奇函数 B．偶函数C．非奇非偶函数 D．既是奇函数又是偶函数
解析：∵函数f(x)＝|sin x|＋cs x的定义域是R，且f(－x)＝|sin (－x)|＋cs (－x)＝|－sin x|＋cs x＝|sin x|＋cs x＝f(x)∴f(x)是偶函数．故选B.
答案：(1)BD　(2)见解析
变式探究　本例(2)中，把条件“偶函数”改为“奇函数”，其它条件不变，结果如何？
方法归纳 (1)已知三角函数的奇偶性求参数范围问题一般利用三角函数的图象特征较简单．(2)利用三角函数的奇偶性与周期性求函数值一般要把自变量转化到已知表达式的区间上求值．
答案：(1)BD　(2)－1
课堂十分钟1．(多选)下列是定义在R上的四个函数图象的一部分，其中是周期函数的是(　　)
解析：对于D，x∈(－1，1)时的图象与其他区间图象不同，不是周期函数．故选ABC.
4．已知函数y＝cs (x－φ)，φ∈[0，π]是奇函数，则φ的值为________．